11.

U dati krug upisati petougao sa jednakim stranama i jednakim uglovima.

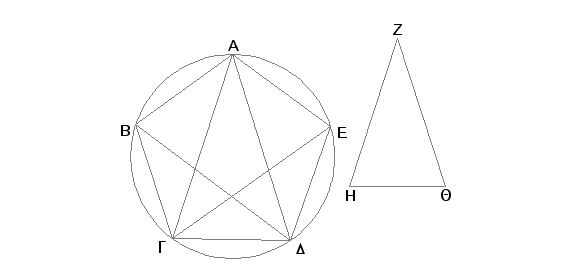
Neka je dat krug ABGDE. Treba u krug ABGDE upisati petougao sa jednakim stranama i jednakim uglovima.
Uzmimo ravnokraki trougao ZHQ sa svakim od uglova kod H i Q dvaput većim od ugla kod Z [IV.10] i upišimo u krug ABGDE trougao AGD sa uglovima jednakim uglovima trougla ZHQ tako da ugao GAD bude jednak uglu kod Z, a svaki od uglova AGD i GDA bude jednak svakom od uglova kod tačaka H i Q [IV.2]; tada je svaki od uglova AGD i GDA dvaput veći od ugla GAD. Prepolovimo svaki od uglova AGD i GDA pravim linijama GE i DB i spojimo AB, BG, (GD), DE, EA.
Kako je svaki od uglova AGD i GDA dvaput veći od ugla GAD, a prave GE i DB polove ih, biće pet uglova DAG, AGE, EGD, GDB, BDA međusobno jednaki. Ali se jednaki uglovi oslanjaju na jednake lukove [III.26], prema tome su pet lukova AB, BG, GD, DE, EA međusobno jednaki. Kako sad jednake lukove stežu jednake prave (tetive) [III.29], biće pet pravih AB, BG, GD, DE, EA međusobno jednake. Prema tome je petougao ABGDE sa jednakim stranama. Tvrdim da ima i jednake uglove. Kako je, naime luk AB jednak luku DE, dodajmo zajednički luk BGD, tada je ceo luk ABGD jednak celom luku EDGB. A na luk ABGD se oslanja ugao AED, a na luk EDGB - ugao BAE, pa je prema tome i ugao BAE jednak uglu AED [III.27]. Iz istih razloga je svaki od uglova ABG, BGD, GDE jednak svakom od uglova BAE i AED. Petougao ABGDE je prema tome sa jednakim uglovima. A dokazano je da je on i sa jednakim stranama.
Na ovaj način je u dati krug upisan petougao sa jednakim stranama i jednakim uglovima. A to je trebalo izvesti.