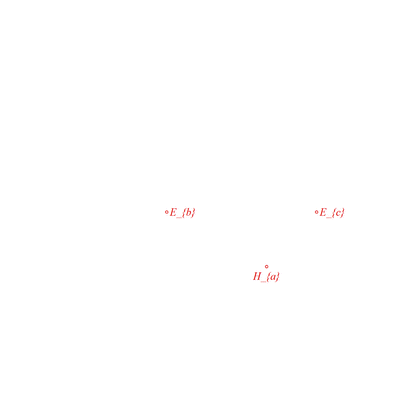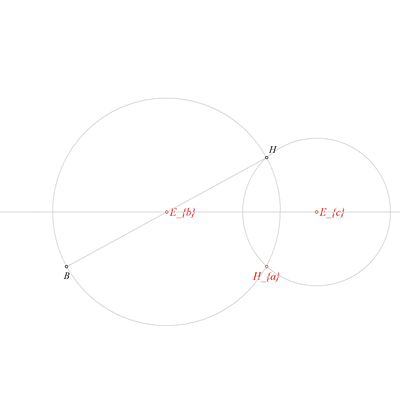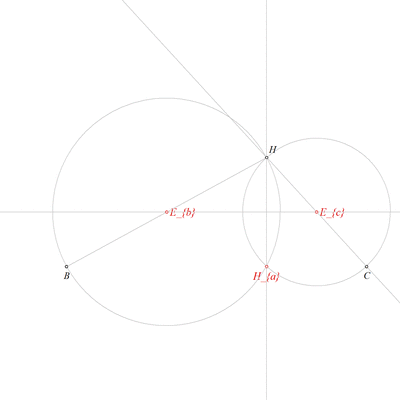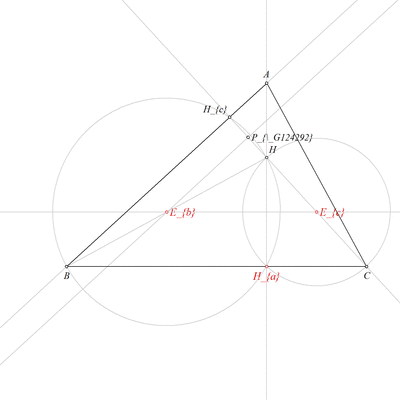Using the point H_a and the point E_b, construct a circle k(E_b,B) (rule W06);

% NDG: points H_a and E_b are not the same

Using the point H_a and the point E_c, construct a circle k(E_c,C) (rule W06);

% NDG: points H_a and E_c are not the same

Using the circle k(E_b,B), the circle k(E_c,C), the point H_a, the point E_b and the point E_c, construct a point H (rule W08);

% NDG: circles k(E_b,B) and k(E_c,C) intersect

% DET: circles k(E_b,B) and k(E_c,C) are not the same points H_a and H must be different

Using the point H and the point E_b, construct a point B (rule W01);

Using the point E_c and the point H, construct a point C (rule W01);

Using the point E_c and the point H, construct a line h_c (rule W02);

% DET: points E_c and H are not the same

Using the point H_a and the point H, construct a line h_a (rule W02);

% DET: points H_a and H are not the same

Using the circle k(E_b,B), the line h_c, the point E_b and the point H, construct a point H_c (rule W05);

% NDG: line h_c and circle k(E_b,B) intersect

% DET: points H and H_c must be different

Using the point B and the point H_c, construct a line c (rule W02);

% DET: points B and H_c are not the same

Using the line h_a and the line c, construct a point A (rule W03);

% NDG: lines h_a and c are not parallel

% DET: lines h_a and c are not the same