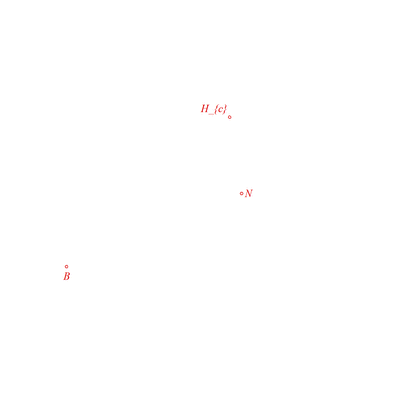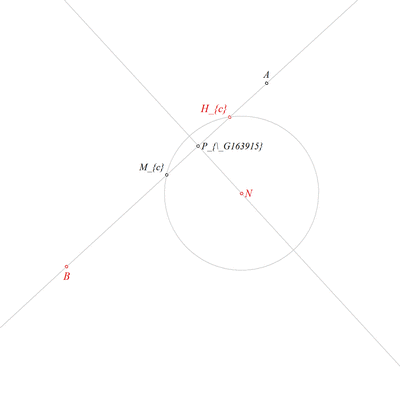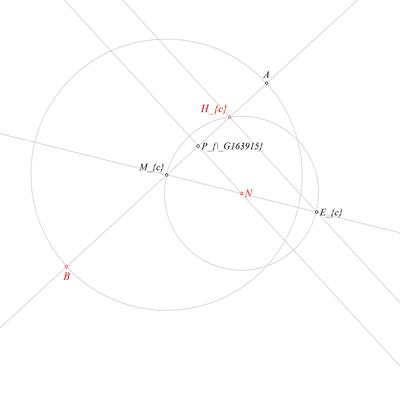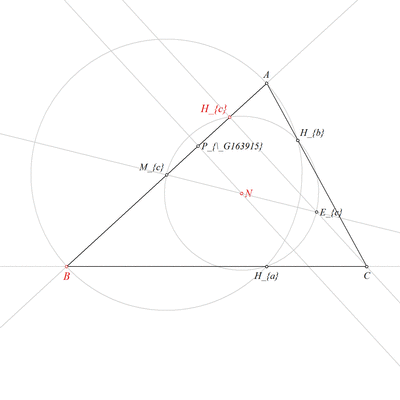Using the point B and the point H_c, construct a line c (rule W02);

% DET: points B and H_c are not the same

Using the point H_c and the point N, construct a circle k(N,M_a) (rule W06);

% NDG: points H_c and N are not the same

Using the circle k(N,M_a), the line c, the point N and the point H_c, construct a point M_c (rule W05);

% NDG: line c and circle k(N,M_a) intersect

% DET: points H_c and M_c must be different

Using the point M_c and the point B, construct a point A (rule W01);

Using the point N and the point M_c, construct a line m(H_aH_b) (rule W02);

% DET: points N and M_c are not the same

Using the circle k(N,M_a), the line m(H_aH_b), the point N and the point M_c, construct a point E_c (rule W05a);

% NDG: line m(H_aH_b) and circle k(N,M_a) intersect

% DET: points M_c and E_c must be different

Using the point E_c and the point H_c, construct a line h_c (rule W02);

% DET: points E_c and H_c are not the same

Using the point B and the point M_c, construct a circle k(M_c,A) (rule W06);

% NDG: points B and M_c are not the same

Using the circle k(N,M_a) and the circle k(M_c,A), construct a point H_a and a point H_b (rule W07);

% NDG: circles k(N,M_a) and k(M_c,A) intersect

% DET: circles k(N,M_a) and k(M_c,A) are not the same

Using the point B and the point H_a, construct a line a (rule W02);

% DET: points B and H_a are not the same

Using the line h_c and the line a, construct a point C (rule W03);

% NDG: lines h_c and a are not parallel

% DET: lines h_c and a are not the same