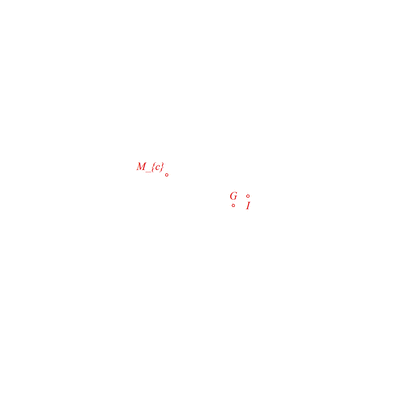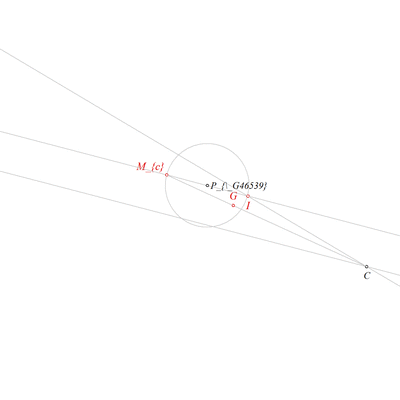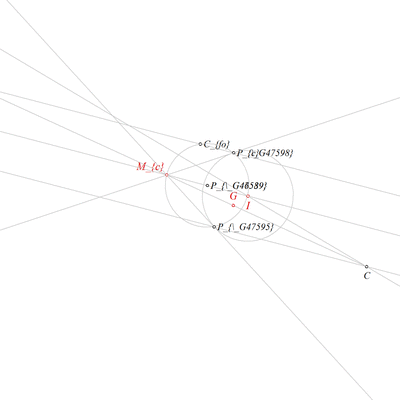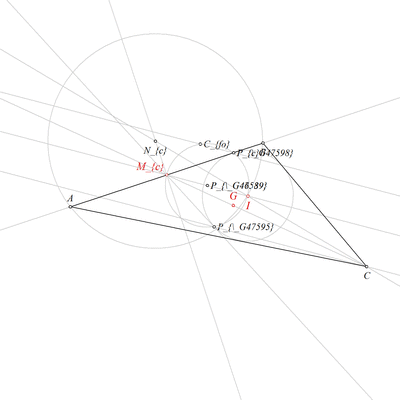Using the point M_c and the point G, construct a point C (rule W01);

Using the point M_c and the point I, construct a line IM_c (rule W02);

% DET: points M_c and I are not the same

Using the point I and the point C, construct a line s_c (rule W02);

% DET: points I and C are not the same

Using the point I and the point M_c, construct a circle k_over(I,M_c) (rule W09);

% NDG: points I and M_c are not the same

Using the point C and the line IM_c, construct a line CP`_c (rule W16);

Using the point M_c, the line CP`<sub>c</sub> and the point C, construct a line h<sub>Mc,-1/1</sub>(CP`_c) (rule W15);

Using the circle k_over(I,M_c) and the line h_Mc,-1/1(CP`_c), construct a point C_fo and a point P_c (rule W04);

% NDG: line h_Mc,-1/1(CP`_c) and circle k_over(I,M_c) intersect

Using the point P_c and the point I, construct a circle k(I,P_a) (rule W06);

% NDG: points P_c and I are not the same

Using the circle k(I,P_a), the point M_c and the point I, construct a line x3 and a line c (rule W12);

% NDG: point M_c is outside the circle k(I,P_a)

Using the point M_c and the line c, construct a line m_c (rule W10b);

Using the line m_c and the line s_c, construct a point N_c (rule W03);

% NDG: lines m_c and s_c are not parallel

% DET: lines m_c and s_c are not the same

Using the point I and the point N_c, construct a circle k(N_c,B) (rule W06);

% NDG: points I and N_c are not the same

Using the circle k(N_c,B) and the line c, construct a point B and a point A (rule W04);

% NDG: line c and circle k(N_c,B) intersect