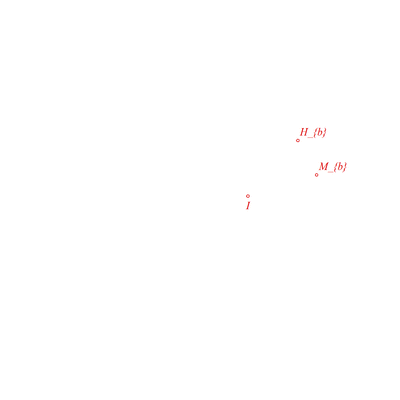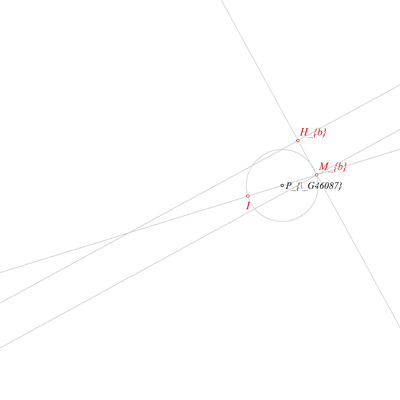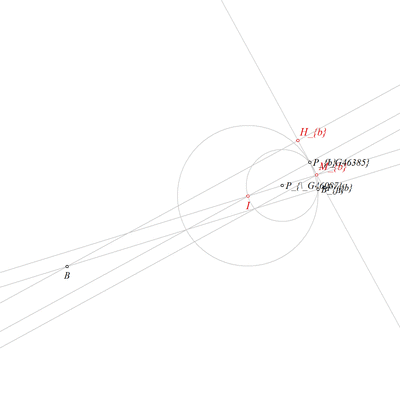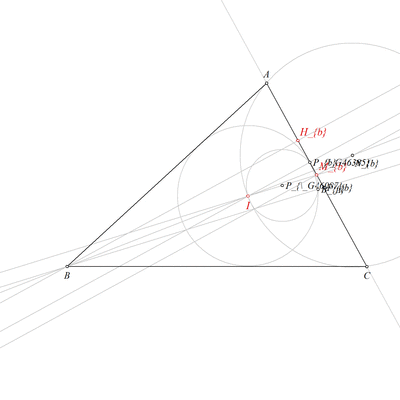Using the point M_b and the point H_b, construct a line b (rule W02);

% DET: points M_b and H_b are not the same

Using the point M_b and the point I, construct a line IM_b (rule W02);

% DET: points M_b and I are not the same

Using the point I and the point M_b, construct a circle k_over(I,M_b) (rule W09);

% NDG: points I and M_b are not the same

Using the point M_b and the line b, construct a line m_b (rule W10b);

Using the point H_b and the line b, construct a line h_b (rule W10b);

Using the point I and the line b, construct a circle k(I,P_a) (rule W11);

% NDG: point I is not incident to the line b

Using the circle k(I,P_a) and the circle k_over(I,M_b), construct a point B_fi and a point P_b (rule W07);

% NDG: circles k(I,P_a) and k_over(I,M_b) intersect

% DET: circles k(I,P_a) and k_over(I,M_b) are not the same

Using the point P_b and the point M_b, construct a point P`_b (rule W01);

Using the point P`<sub>b</sub> and the line IM<sub>b</sub>, construct a line BP`_b (rule W16);

Using the line BP`_b and the line h_b, construct a point B (rule W03);

% NDG: lines BP`_b and h_b are not parallel

% DET: lines BP`_b and h_b are not the same

Using the point I and the point B, construct a line s_b (rule W02);

% DET: points I and B are not the same

Using the line m_b and the line s_b, construct a point N_b (rule W03);

% NDG: lines m_b and s_b are not parallel

% DET: lines m_b and s_b are not the same

Using the point I and the point N_b, construct a circle k(N_b,A) (rule W06);

% NDG: points I and N_b are not the same

Using the circle k(N_b,A) and the line b, construct a point A and a point C (rule W04);

% NDG: line b and circle k(N_b,A) intersect