Najveće rastojanje između dve tačke nekog skupa se naziva dijametar skupa tačaka.
Rešenje grubom silom podrazumeva izračunavanje rastojanja između svih parova tačaka i složenosti je \(O(n^2)\).
Efikasnije rešenje započinjemo opaskom da se dve najdalje tačke moraju nalazi na konveksnom omotaču skupa tačaka. Dijametar skupa tačaka jednak je dijametru njegovog konveksnog omotača. Zato u prvoj fazi algoritma konstruišemo konveksni omotač datog skupa tačaka (što Grejemovim algoritmom možemo uraditi u vremenu \(O(n \log{n})\)).
Nakon toga možemo proveravati sve parove tačaka na konveksnom omotaču, što u mnogim slučajevima dovodi do ubrzanja, međutim, složenost najgoreg slučaja ne bi bila popravljena, jer svih \(n\) tačaka polaznog skupa može ležati na konveksnom omotaču. Stoga ćemo analizu tačaka na konveksnom omotaču vršiti pažljivije.
Za svako teme konveksnog omotača ćemo odrediti njemu najdalje teme na omotaču. Iako možda na prvi pogled deluje da rastojanja temena od fiksiranog temena na konveksnom omotaču imaju neko svojstvo monotonosti dok redom obilazimo temena mnogougla, to nije slučaj (kao što je ilustrovano na slici 1).
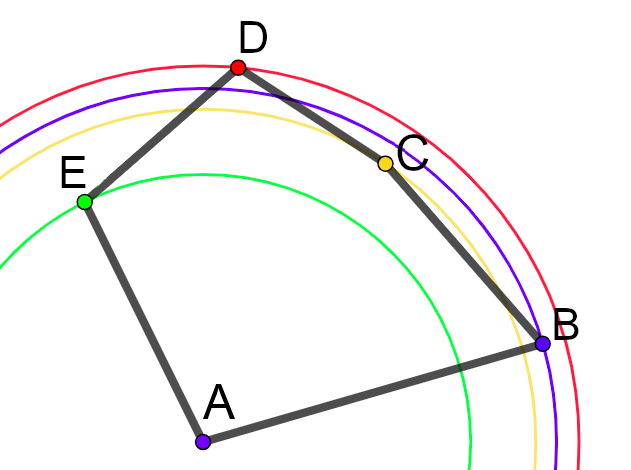
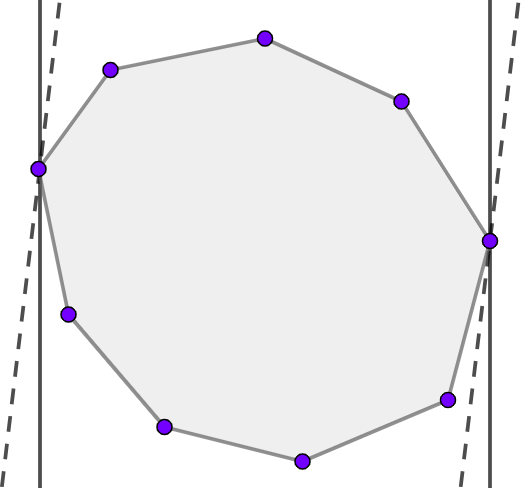
Kroz par međusobno najdaljih temena se mogu povući dve paralelne prave tako da se ceo mnogougao nalazi između te dve prave (slika 2) — za takva dva temena kažemo da su antipodalna. Te paralelne prave ne moraju biti jedinstvene. Teme najdalje od datog temena mu je sigurno antipodalno, međutim, moguće je da postoji više temena koja su antipodalna datom temenu. Algoritam ćemo organizovati tako što ćemo za svako teme obilaziti njemu antipodalna temena i među njima tražiti ono najdalje od datog.
Kako odrediti sva temena koja su antipodalna datom temenu \(P\)? Prava koja dokazuje antipodalnost tj. prava koja prolazi kroz \(P\) sa čije se jedne strane nalazi ceo poligon mora ležati između pravih koje spajaju \(P\) sa njemu susednim temenima poligona (na slici 3, to su prave \(PQ\) i \(PR\)) – pravu kroz \(P\) možemo rotirati sve dok ne dostigne jednu od te dve prave. Svaku od tako dobijenih pravih možemo paralelno pomerati preko mnogougla, sve dok ne dostigne teme mnogougla koje je od nje najdalje i to teme će sigurno biti anipodalno temenu \(P\) (na slici 3, antipodalna temena temenu \(P\) su temena \(A\), \(B\), \(C\), \(D\) i \(E\)).
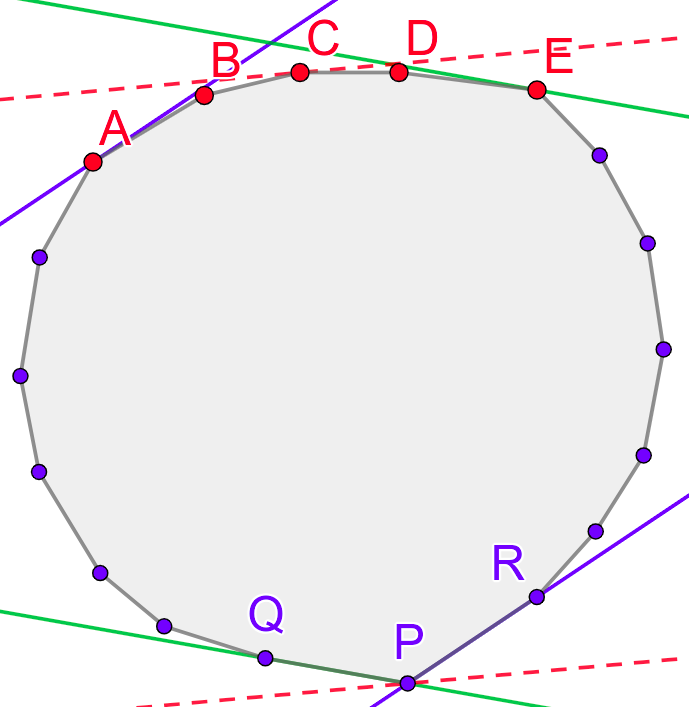
Problem se, dakle, svodi na to se za svaku stranicu mnogougla pronađe teme koje je najdalje od nje. Kada se stranice obilaze redom (na primer, u pozitivnom matematičkom smeru) i najdalja temena od tih stranica se pomeraju redom, u istom smeru. Dakle, za razliku od određivanja najdaljeg temena od svakog temena mnogougla, najdalje teme od svake stranice mnogougla ima svojstvo monotonosti, pa se određivanje tih temena može zasnovati na algoritmu dva pokazivača (jedan će se kretati redom kroz stranice, a drugi redom kroz njima najdalja temena). Krećemo od proizvoljne stranice mnogougla i grubom silom određujemo teme koje je najdalje od nje. U svakom koraku se pomeramo na sledeću stranicu, a zatim pomeramo najdalje teme sve dok rastojanje od te sledeće stranice raste. Rastojanje možemo lako izračunati kao količnik površine trougla koji čine ta stranica i tekuće teme i dužine te stranice, a pošto se stranica ne menja, pokazivač možemo pomerati sve dok površina trougla raste. Tokom tog pomeranja prolazimo kroz sve antipodalne tačke početnom temenu tekuće stranice, pa računajući njihovo rastojanje od tog temena možemo odrediti najdalje teme od tog temena, pa samim tim i dve najdalje tačke početnog skupa.
Složenost određivanja najdaljeg temena od polazne stranice zahteva jedan obilazak temena mnogougla i složenosti je \(O(n)\). Svaki od pokazivača se pomera u istom smeru i obilazi sva temena mnogougla po jednom, pa je ukupna složenost druge faze algoritma \(O(n)\). Ukupnom složenošću, dakle, dominira određivanje konveksnog omotača početnog skupa, koje je složenosti \(O(n\log{n})\).
double najdaljiParTacaka(const vector<Tacka>& tacke) {
// odredjujemo konveksni omotac i broj njegovih tacaka
vector<Tacka> omotac = konveksniOmotac(tacke);
int m = omotac.size();
// specijalni slucajevi kada omotac ima manje od 3 tacke
if (m == 1) return 0.0;
if (m == 2) return rastojanje(omotac[0], omotac[1]);
// odredjujemo najdalju tacku od duzi Qm-1Q0
int najdaljaTacka = 2;
for (int i = 3; i < omotac.size(); i++)
if (povrsina(omotac[m-1], omotac[0], omotac[i]) >
povrsina(omotac[m-1], omotac[0], omotac[najdaljaTacka]))
najdaljaTacka = i;
// prva antipodalna tacka od tacke Q0
double maxRastojanje = rastojanje(omotac[0], omotac[najdaljaTacka]);
// obradjujemo ostale tacke Qi
for (int i = 0; i < m; i++) {
// do sada je obradjena prva antipodalna tacka tacke Qi
// sada redom obradjujemo njene ostale antipodalne tacke
// njih nalazimo trazeci najdalju tacku od duzi QiQi+1
while (povrsina(omotac[i], omotac[(i+1)%m], omotac[najdaljaTacka]) <=
povrsina(omotac[i], omotac[(i+1)%m], omotac[(najdaljaTacka+1)%m])) {
// za svaku antipodalnu tacku od Qi odrequjemo rastojanje od Qi
maxRastojanje = max(maxRastojanje,
rastojanje(omotac[i], omotac[najdaljaTacka]));
// i sledeca tacka je antipodalna tacki Qi
najdaljaTacka = (najdaljaTacka + 1) % n;
}
}
return maxRastojanje;
}#include <iostream>
#include <iomanip>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
struct Tacka {
int x, y;
};
// moguce orijentacije trojke tacaka
enum Orijentacija {POZITIVNA, KOLINEARNE, NEGATIVNA};
Orijentacija orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
int d = (B.x-A.x)*(C.y-A.y) - (C.x-A.x)*(B.y-A.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
double kvadratRastojanja(const Tacka& A, const Tacka& B) {
int dx = A.x - B.x;
int dy = A.y - B.y;
return dx*dx + dy*dy;
}
double rastojanje(const Tacka& A, const Tacka& B) {
return sqrt(kvadratRastojanja(A, B));
}
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// trazimo ekstremnu tacku sa maksimalnom x koordinatom,
// u slucaju da ima vise tacaka sa maksimalnom x koordinatom
// biramo onu sa najmanjom y koordinatom
auto max = max_element(begin(tacke), end(tacke),
[](const Tacka& t1, const Tacka& t2) {
return t1.x < t2.x ||
(t1.x == t2.x && t1.y > t2.y);
});
// dovodimo je na početak niza
swap(*begin(tacke), *max);
const Tacka& t0 = tacke[0];
// sortiramo ostatak niza (tačke sortiramo na osnovu ugla koji
// zaklapaju u odnosu horizontalnu polupravu koja polazi nadesno
// iz ekstremne tacke), a kolinearne na osnovu rastojanja te tacke
sort(next(begin(tacke)), end(tacke),
[t0](const Tacka& t1, const Tacka& t2) {
Orijentacija o = orijentacija(t0, t1, t2);
if (o == KOLINEARNE)
return kvadratRastojanja(t0, t1) <= kvadratRastojanja(t0, t2);
return o == POZITIVNA;
});
// obradjujemo tacke u sortiranom redosledu izbacujuci prethodne sve
// dok se tekuca tacka sa dve poslednje ne cini levi zaokret
vector<Tacka> omotac;
omotac.push_back(tacke[0]);
omotac.push_back(tacke[1]);
for (size_t i = 2; i < tacke.size(); i++) {
while (omotac.size() >= 2 &&
orijentacija(omotac[omotac.size()-2],
omotac[omotac.size()-1],
tacke[i]) != POZITIVNA)
omotac.pop_back();
omotac.push_back(tacke[i]);
}
return omotac;
}
// dvostruka povrsina trougla ABC
int povrsina(const Tacka& A, const Tacka& B, const Tacka& C) {
return abs((B.x - A.x)*(C.y - A.y) - (B.y - A.y)*(C.x - A.x));
}
double najdaljiParTacaka(const vector<Tacka>& tacke) {
// odredjujemo konveksni omotac i broj njegovih tacaka
vector<Tacka> omotac = konveksniOmotac(tacke);
int m = omotac.size();
// specijalni slucajevi kada omotac ima manje od 3 tacke
if (m == 1) return 0.0;
if (m == 2) return rastojanje(omotac[0], omotac[1]);
// odredjujemo najdalju tacku od duzi Qm-1Q0
int najdaljaTacka = 2;
for (int i = 3; i < omotac.size(); i++)
if (povrsina(omotac[m-1], omotac[0], omotac[i]) >
povrsina(omotac[m-1], omotac[0], omotac[najdaljaTacka]))
najdaljaTacka = i;
// prva antipodalna tacka od tacke Q0
double maxRastojanje = rastojanje(omotac[0], omotac[najdaljaTacka]);
// obradjujemo ostale tacke Qi
for (int i = 0; i < m; i++) {
// do sada je obradjena prva antipodalna tacka tacke Qi
// sada redom obradjujemo njene ostale antipodalne tacke
// njih nalazimo trazeci najdalju tacku od duzi QiQi+1
while (povrsina(omotac[i], omotac[(i+1)%m], omotac[najdaljaTacka]) <=
povrsina(omotac[i], omotac[(i+1)%m], omotac[(najdaljaTacka+1)%m])) {
// za svaku antipodalnu tacku od Qi odrequjemo rastojanje od Qi
maxRastojanje = max(maxRastojanje,
rastojanje(omotac[i], omotac[najdaljaTacka]));
// i sledeca tacka je antipodalna tacki Qi
najdaljaTacka = (najdaljaTacka + 1) % n;
}
}
return maxRastojanje;
}
int main() {
int n;
cin >> n;
vector<Tacka> tacke(n);
for (int i = 0; i < n; i++)
cin >> tacke[i].x >> tacke[i].y;
cout << fixed << showpoint << setprecision(5)
<< najdaljiParTacaka(tacke) << endl;
}