
Konveksni omotač (engl. convex hull) konačnog skupa tačaka definiše se kao najmanji konveksni mnogougao takav da sve tačke tog skupa pripadaju unutrašnjosti ili stranicama tog mnogougla (slika 1). Definisaćemo i da je za jednu tačku konveksni omotač ta tačka, a za par tačaka duž koja ih spaja. Jasno je iz definicije da je konveksni omotač tri nekolinearne tačke trougao kome su te tačke temena. Zabranićemo da konveksni omotač sadrži kolinearne tačke i tada za svaki skup tačaka postoji jedinstven konveksni omotač. Konveksni omotač se predstavlja na isti način kao bilo koji mnogougao — nizom svojih uzastopnih temena.

U narednom apletu se prikazuje konveksni omotač datog skupa tačaka. Pomeranjem tačaka možete promeniti i konveksni omotač.
Kao što smo već videli, obrada konveksnih mnogouglova jednostavnija je od obrade proizvoljnih mnogouglova. Na primer, provera pripadnosti tačke unutrašnjosti proizvoljnog prostog \(n\)-tougla je složenosti \(O(n)\), dok je ispitivanje pripadnosti tačke unutrašnjosti konveksnog \(n\)-tougla složenosti \(O(\log n)\).
Iz uslova da je konveksni omotač najmanji konveksni mnogougao sa datim svojstvima, sledi da su temena konveksnog omotača neke od tačaka iz zadatog skupa. Kazaćemo da tačka pripada omotaču ako je teme omotača. Ako zanemarimo trivijalne slučajeve kada polazni skup ne sadrži bar tri nekolinearne tačke, konveksni omotač može se sastojati od najmanje tri, a najviše \(n\) tačaka (slika 2).

Konveksni omotači imaju široku primenu (na primer, u praćenju širenja epidemija, modelovanju glatkih krivih, smanjenju broja boja na slici, planiranju kretanja robota, kao gradivni element u drugim algoritmima, kao što je recimo traženje dijametra skupa tačaka), pa su zbog toga razvijeni mnogobrojni algoritmi za njihovu konstrukciju. Razmotrimo problem navigacije robota u ravni od tačke \(A\) do tačke \(B\). Najjednostavniji način da robot realizuje ovo kretanje je pravolinijski, duž duži \(AB\). Međutim, na ovoj pravolinijskoj putanji se može naći neka od prepreka. Stoga se svaka od prepreka može uzorkovati tačkom u ravni, a onda napraviti konveksni omotač svih ovih tačaka. Za putanju koja ne seče ovaj omotač se garantuje da neće biti sudara robota sa nekom od prepreka.
U nastavku ćemo razmotriti nekoliko različitih rešenja narednog problema.
Problem. Konstruisati konveksni omotač zadatih \(n\) tačaka u ravni.
Kao i obično, pokušaćemo najpre sa direktnim induktivnim pristupom. Konveksni omotač za jednu tačku je jednočlan i to može biti baza indukcije. Pretpostavimo sledeću induktivnu hipotezu.
Induktivna hipoteza. Umemo da konstruišemo konveksni omotač skupa koji sadrži manje od \(n\) tačaka.
Pokušajmo da konstruišemo konveksni omotač skupa od \(n\) tačaka. Na koji način \(n\)-ta tačka može da promeni konveksni omotač prvih \(n-1\) tačaka? Postoje dva moguća slučaja:
Prilikom dodavanja svake nove tačke potrebno je, dakle, rešiti dva potproblema: utvrđivanje da li je nova tačka unutar omotača i proširivanje omotača novom tačkom.
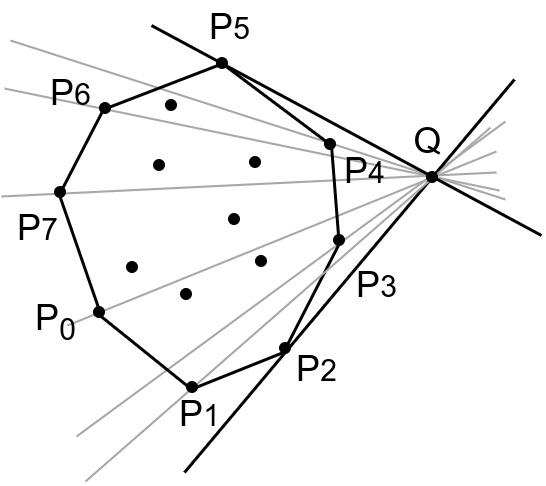
Stvar se može uprostiti pogodnim izborom \(n\)-te tačke, tako da ne moramo eksplicitno vršiti proveru da li ona pripada prethodnom omotaču. Zvuči primamljivo pokušati da uvek biramo tačku unutar omotača, jer tada ne moramo da menjamo omotač da bi se proširila induktivna hipoteza; to, međutim, nije uvek moguće jer u nekim slučajevima sve tačke polaznog skupa pripadaju konveksnom omotaču (2, levo). Sasvim suprotna mogućnost je da se u svakom koraku bira tačka za koju znamo da ne pripada unutrašnjosti tekućeg omotača. To će biti zadovoljeno ako se u svakom koraku bira neka ekstremna tačka novog mnogougla, pri čemu nam taj izbor, kao što ćemo videti, dodatno uprošćava postupak ažuriranja konveksnog omotača. Podsetimo se, ekstremne tačke su se pokazale uspešne pri rešavanju problema konstrukcije prostog mnogougla. Ekstremna tačka koja se u tom problemu koristila je ona sa maksimalnom \(x\)-koordinatom (pri čemu se ako ima više takvih tačaka bira ona sa minimalnom \(y\)-koordinatom). Da bi se u svakom koraku koristila ekstremna tačka, potrebno je tačke obrađivati u neopadajućem redosledu \(x\)-koordinata (pri čemu tačke sa istom \(x\)-koordinatom treba obrađivati u nerastućem redosledu \(y\)-koordinata), što se najlakše postiže ako se u startu tačke sortiraju na taj način. Tada zapravo koristimo prethodnu induktivnu hipotezu, ali tako da je uvek primenjujemo na skup prethodnih tačaka u sortiranom redosledu. Neka je tekuća tačka kojom se proširuje konveksni omotač konstruisan od početnih \(n-1\) tačaka tačka \(Q\), koja je ekstremna u tekućem skupu od \(n\) tačaka. Tačka \(Q\) mora biti teme novog konveksnog omotača. Pitanje je kako promeniti konveksni omotač ostalih \(n-1\) tačaka tako da novi omotač obuhvati tačku \(Q\). Potrebno je najpre pronaći temena starog omotača koja su u unutrašnjosti novog omotača (\(P_3\) i \(P_4\) u primeru na slici 3) i ukloniti ih, a zatim je potrebno umetnuti novo teme \(Q\) između dva postojeća (\(P_2\) i \(P_5\) na slici 3).
Određivanje tačaka tekućeg omotača koje treba da budu zamenjene tačkom \(Q\) može se izvršiti korišćenjem pravih oslonca. Prava oslonca (engl. supporting plane) konveksnog mnogougla je prava koja sadrži bar jednu tačku mnogougla i sve ostale tačke mnogougla se nalaze sa iste strane te prave. U našem slučaju su bitne prave oslonca koje sadrže tačku \(Q\). Na primer, na slici 3 prave \(QP_2\) i \(QP_5\) su dve prave oslonca i polaznog i proširenog konveksnog mnogougla. Obično samo jedno teme mnogougla povezivanjem sa \(Q\) određuje pravu oslonca (postoji i specijalni slučaj kad više temena mnogougla leži na pravi oslonca, koji ćemo na trenutak zanemariti). Mnogougao leži između dve prave oslonca, što ukazuje na to na koji način treba izvesti modifikaciju omotača. Prave oslonca zahvataju minimalni i maksimalni ugao sa horizontalnom polupravom \(p\) koja se iz tačke \(Q\) prostire u pozitivnom smeru \(x\) ose, među svim pravama koje sadrže tačku \(Q\) i neko teme mnogougla. Da bismo odredili ta dva temena, potrebno je da razmotrimo poluprave iz tačke \(Q\) ka svim temenima, da izračunamo uglove sa \(p\), i među tim uglovima izaberemo minimalan (čime dobijamo tačku \(P_i\)) i maksimalan (čime dobijamo tačku \(P_j\)). Kao što je pokazano lemom 59, umesto eksplicitnog računanja uglova, moguće ih je samo upoređivati na osnovu orijentacije (ugao koji poluprava \(QP_m\) zahvata sa polupravom \(p\) manji je od ugla koji poluprava \(QP_n\) zahvata sa \(p\) ako i samo ako je trojka \(QP_mP_n\) pozitivno orijentisana). U specijalnom slučaju se može desiti da su neke tačke \(P_m\) i \(P_n\) kolinearne sa tačkom \(Q\) i tada uzimamo onu od njih koja se nalazi dalje od \(Q\) (jer pretpostavljamo da je konveksni omotač zatvoren mnogougao i da pošto bliža tačka pripada stranici, pripada i omotaču).
Posle pronalaženja dva ekstremna temena \(P_i\) i \(P_j\) modifikovani omotač dobijamo tako što onaj niz temena između \(P_i\) i \(P_j\) (bez \(P_i\) i \(P_j\)) čije su tačke sa iste strane prave \(P_iP_j\) kao i tačka \(Q\) zamenimo tačkom \(Q\) (ako je taj niz prazan, samo se umeće nova tačka \(Q\)).
Primer 162. U primeru prikazanom na slici 3 temena \(P_3\) i \(P_4\) se nalaze se sa iste strane prave \(P_5P_2\) kao i tačka \(Q\), pa se niz temena starog omotača \([P_3, P_4]\) zamenjuje novim temenom \(Q\). Tačke \(P_0\) i \(P_1\) su sa suprotne strane prave \(P_5P_2\) od tačke \(Q\), pa one ostaju deo konveksnog omotača.
Da bi se realizovao prethodni algoritam, nije neophodno eksplicitno ispitivati koji od dva niza tačaka između \(P_i\) i \(P_j\) leži sa iste strane prave \(P_iP_j\) kao i \(Q\). Naime, ako sva temena trenutnog konveksnog omotača čuvamo u redosledu pozitivne orijentacije, pošto je tačka \(Q\) ekstremna i nalazi se desno od prave \(P_iP_j\), tačke između \(P_j\) i \(P_i\) će biti sa iste strane prave \(P_iP_j\) kao i \(Q\), dok će tačke između \(P_i\) i \(P_j\) biti sa suprotne strane. Dakle, uvek je potrebno niz tačaka od \(P_{j+1}\) do \(P_{i-1}\) zameniti tačkom \(Q\) (pri čemu se uvećanje i umanjenje indeksa računa ciklično, tj. po modulu \(n\)). Ako su tačke \(P_j\) i \(P_i\) susedne, taj niz može biti i prazan.
U narednom apletu možete videti kako funkcioniše ovaj algoritam.
U nastavku je prikazana C++ implementacija ovog algoritma.
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// sortiramo tacke po x koordinati neopadajuce,
// ako postoje dve tacke sa istom vrednoscu x koordinate
// manjom smatramo onu sa vecom y koordinatom
sort(begin(tacke), end(tacke),
[](const Tacka &p1, const Tacka &p2) {
return (p1.x < p2.x) || (p1.x == p2.x && p1.y > p2.y);
});
// u konveksni omotac dodajemo prvu tacku
vector<Tacka> omotac;
omotac.push_back(tacke[0]);
// dodajemo jednu po jednu tacku u omotac u redosledu rastucih x koordinata
for (int k = 1; k < tacke.size(); k++) {
// trazimo gornju pravu oslonca
// to je prava P_kP_i tako da za svako ii vazi
// da trojka tacaka {P_k, P_i, P_ii} ima pozitivnu orijentaciju ili su
// tacke kolinearne, ali je P_ii dalje od tacke P_k nego P_i
int i = 0;
for (int ii = 0; ii < omotac.size(); ii++) {
int o = orijentacija(tacke[k], omotac[i], omotac[ii]);
if (o == NEGATIVNA ||
(o == KOLINEARNE && kvadratRastojanja(tacke[k], omotac[i]) <
kvadratRastojanja(tacke[k], omotac[ii])))
i = ii;
}
// trazimo donju pravu oslonca
// to je prava P_kP_j tako da za svako jj vazi
// da trojka tacaka {P_k, P_jj, P_j} ima pozitivnu orijentaciju ili su
// tacke kolinearne, ali je P_jj dalje od tacke P_k nego P_j
int j = 0;
for (int jj = 0; jj < omotac.size(); jj++) {
int o = orijentacija(tacke[k], omotac[jj], omotac[j]);
if (o == NEGATIVNA ||
(o == KOLINEARNE && kvadratRastojanja(tacke[k], omotac[j]) <
kvadratRastojanja(tacke[k], omotac[jj])))
j = jj;
}
zameni(omotac, (j + 1) % omotac.size(), i, tacke[k]);
}
return omotac;
}
// podniz niza a_i,...,a_{j-1} menjamo elementom x
// ako je i > j, brisu se elementi do kraja, pa zatim sa pocetka niza
void zameni(vector<Tacka>& a, int i, int j, const Tacka& x) {
if (i < j)
// ako je i < j, onda su tacke koje brisemo susedne
a.erase(a.begin() + i, a.begin() + j);
else if (i > j) {
// ako je j > i, onda elemente brisemo iz dva dela
a.erase(a.begin() + i, a.end());
a.erase(a.begin(), a.begin() + j);
}
// ako je i = j, onda se ne brise nista
// ubacujemo novi broj x
a.insert(a.begin() + i, x);
}# include <iostream> {.unnumbered .unlisted}
# include <vector> {.unnumbered .unlisted}
# include <algorithm> {.unnumbered .unlisted}
using namespace std;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
int x, y;
};
enum Orijentacija { POZITIVNA, NEGATIVNA, KOLINEARNE };
Orijentacija orijentacija(const Tacka& t0, const Tacka& t1, const Tacka& t2) {
long long d = (long long)(t1.x-t0.x)*(long long)(t2.y-t0.y) -
(long long)(t2.x-t0.x)*(long long)(t1.y-t0.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
long long kvadratRastojanja(const Tacka& t1, const Tacka& t2) {
long long dx = t1.x - t2.x, dy = t1.y - t2.y;
return dx*dx + dy*dy;
}
// podniz niza a_i,...,a_{j-1} menjamo elementom x
// ako je i > j, brisu se elementi do kraja, pa zatim sa pocetka niza
void zameni(vector<Tacka>& a, int i, int j, const Tacka& x) {
if (i < j)
// ako je i < j, onda su tacke koje brisemo susedne
a.erase(a.begin() + i, a.begin() + j);
else if (i > j) {
// ako je j > i, onda elemente brisemo iz dva dela
a.erase(a.begin() + i, a.end());
a.erase(a.begin(), a.begin() + j);
}
// ako je i = j, onda se ne brise nista
// ubacujemo novi broj x
a.insert(a.begin() + i, x);
}
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// sortiramo tacke po x koordinati neopadajuce,
// ako postoje dve tacke sa istom vrednoscu x koordinate
// manjom smatramo onu sa vecom y koordinatom
sort(begin(tacke), end(tacke),
[](const Tacka &p1, const Tacka &p2) {
return (p1.x < p2.x) || (p1.x == p2.x && p1.y > p2.y);
});
// u konveksni omotac dodajemo prvu tacku
vector<Tacka> omotac;
omotac.push_back(tacke[0]);
// dodajemo jednu po jednu tacku u omotac u redosledu rastucih x koordinata
for (int k = 1; k < tacke.size(); k++) {
// trazimo gornju pravu oslonca
// to je prava P_kP_i tako da za svako ii vazi
// da trojka tacaka {P_k, P_i, P_ii} ima pozitivnu orijentaciju ili su
// tacke kolinearne, ali je P_ii dalje od tacke P_k nego P_i
int i = 0;
for (int ii = 0; ii < omotac.size(); ii++) {
int o = orijentacija(tacke[k], omotac[i], omotac[ii]);
if (o == NEGATIVNA ||
(o == KOLINEARNE && kvadratRastojanja(tacke[k], omotac[i]) <
kvadratRastojanja(tacke[k], omotac[ii])))
i = ii;
}
// trazimo donju pravu oslonca
// to je prava P_kP_j tako da za svako jj vazi
// da trojka tacaka {P_k, P_jj, P_j} ima pozitivnu orijentaciju ili su
// tacke kolinearne, ali je P_jj dalje od tacke P_k nego P_j
int j = 0;
for (int jj = 0; jj < omotac.size(); jj++) {
int o = orijentacija(tacke[k], omotac[jj], omotac[j]);
if (o == NEGATIVNA ||
(o == KOLINEARNE && kvadratRastojanja(tacke[k], omotac[j]) <
kvadratRastojanja(tacke[k], omotac[jj])))
j = jj;
}
zameni(omotac, (j + 1) % omotac.size(), i, tacke[k]);
}
return omotac;
}
int main() {
int n;
cin >> n;
vector<Tacka> tacke(n);
for (int i = 0; i < n; i++)
cin >> tacke[i].x >> tacke[i].y;
vector<Tacka> omotac = konveksniOmotac(tacke);
cout << omotac.size() << endl;
for (const Tacka& t : omotac)
cout << t.x << " " << t.y << endl;
return 0;
}Primetimo da se u funkciji sortira dati niz tačaka, što znači da argument funkcije nije konstantan. Ako bismo insistirali da se niz ne sme menjati tokom izračunavanja omotača (što je korisna praksa), morali bismo napraviti sortiranu kopiju niza unutar funkcije, čime bi se dobio malo neefikasniji algoritam. Određivanje pravih oslonca se suštinski sprovodi algoritmom određivanja pozicije maksimalnog tj. minimalnog elementa, pa ga je moguće implemenirati i bibliotečkim funkcijama max_element ili min_element.
Razmotrimo složenost ovog algoritma. Prvo se sortira niz temena, za šta je potrebno vreme \(O(n\log{n})\). Za svaku novu tačku koja se dodaje skupu treba izračunati uglove koje grade prave određene tačkom \(Q\) i svakim od temena prethodnog omotača i \(x\)-osa, pronaći među njima minimalni i maksimalni ugao, izbaciti neka temena iz prethodnog omotača i dodati novo teme. Dakle, složenost dodavanja \(k\)-te tačke u tekući skup tačaka je \(O(k)\), a ukupno razmatramo \(n\) tačaka pa se složenost ovog dela algoritma može opisati rekurentnom jednačinom \(T(n)=T(n-1)+O(n)\) čije je rešenje \(O(n^2)\). Pošto je vreme sortiranja \(O(n\log{n})\) asimptotski manje od vremena \(O(n^2)\) potrebnog za ostale operacije, ono ne utiče na ukupnu složenost \(O(n^2)\). Naglasimo i da izbor strukture podataka za čuvanje trenutnog niza temena konveksnog mnogougla (liste ili vektora) ne utiče na asimptotsku složenost (složenost funkcije zameni bi mogla biti snižena kada bi se koristila lista, ali bi asimptotska složenost ostala kvadratna).
Na koji način se opisani algoritam može poboljšati? Kad proširujemo mnogougao teme po teme, dosta vremena trošimo na formiranje konveksnih omotača od tačaka za koje će se kasnije možda pokazati da su unutrašnje za konačni konveksni omotač. Može li se to izbeći? Umesto da pravimo konveksne omotače podskupova datog skupa tačaka, možemo da posmatramo kompletan skup tačaka i da direktno pravimo njegov konveksni omotač. Može se, kao i u prethodnom algoritmu, krenuti od ekstremne tačke. U principu, svejedno je koja se ekstremna tačka koristi. Da bismo ilustrovali malo drugačiji pristup od dosadašnjih rešenja, možemo, na primer, krenuti od tačke sa najmanjom vrednošću \(x\) koordinate, a ako ih ima više one među njima koja ima najmanju \(y\) koordinatu. Kao što smo već pomenuli, ekstremna tačka uvek pripada konveksnom omotaču. Ideja je da se u svakom koraku u omotač doda naredno teme koje je deo konačnog konveksnog omotača (pri čemu temena obilazimo, na primer, u negativnom matematičkom smeru). Kako nalazimo narednu stranicu konveksnog omotača? Jedno teme te stranice biće poslednja tačka do sada određenog dela konveksnog omotača. Da bismo odredili drugo teme stranice, analiziraćemo sve tačke i tražiti onu koja daje duž koja sa prethodnom duži gradi što veći ugao. Primetimo da prilikom određivanja prve stranice mnogougla ne postoji prethodna duž, te u tom slučaju tražimo duž koja gradi maksimalni ugao sa npr. negativnim smerom \(y\) ose.
Neka je \(P_t\) tekuća tačka u konveksnom omotaču. Obrađivaćemo preostale tačke i suštinski primenjivati algoritam određivanja maksimuma. Pretpostavićemo da se maksimalni ugao postiže za neku tačku \(P_l\) različitu od \(P_t\). Zatim ćemo redom obrađivati sve ostale tačke. Analogno lemi 59, umesto računanja uglova možemo upotrebiti orijentaciju.
Postupak se završava kada se ustanovi da je tačka koja određuje najveći ugao sa prethodnom tačkom jednaka početnoj tački. Koraci u izvršavanju ovog algoritma za jedan skup tačaka su prikazani na slici 4.

Ovaj algoritam se iz razumljivih razloga zove uvijanje poklona (engl. gift wrapping algorithm). Polazi se od jednog temena “poklona”, i onda se on uvija u konveksni omotač pronalaženjem temena po temena omotača. Poznat je i pod nazivom Džarvisov1 marš (engl. Jarvis March algorithm), po naučniku koji ga je opisao u radu 1973. godine.
Algoritam uvijanja poklona je direktna posledica primene sledeće induktivne hipoteze (po \(k\)):
Induktivna hipoteza. Za zadati skup od \(n\) tačaka u ravni, umemo da pronađemo konveksni put dužine \(k<n\) koji je deo konačnog konveksnog omotača datog skupa tačaka.
Kod ove hipoteze naglasak je na proširivanju puta, a ne omotača. Umesto da pronalazimo konveksne omotače podskupova, mi pronalazimo deo konačnog konveksnog omotača.
U narednom apletu možete videti kako funkcioniše ovaj algoritam.
Algoritam uvijanja poklona je moguće implementirati na sledeći način:
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// odredjujemo redni broj ekstremne tacke (one sa najmanjom x koordinatom)
auto cmp = [] (const Tacka& t1, const Tacka& t2) {
return t1.x < t2.x || (t1.x == t2.x && t1.y < t2.y);
};
int prva = distance(begin(tacke),
min_element(begin(tacke), end(tacke), cmp));
// niz tacaka koje cine omotac
vector<Tacka> omotac;
// krecemo od ekstremne tacke
int tekuca = prva;
do {
omotac.push_back(tacke[tekuca]);
// krecemo obradu od prve tacke u nizu, osim ako je prva tacka
// bas ekstremna; u tom slucaju krecemo od druge tacke
int naredna = tekuca == 0 ? 1 : 0;
// odredjujemo narednu tacku u omotacu, zahtevajuci da se sve
// ostale tacke nalaze sa desne strane prave odredjene tekucom i
// tom narednom tackom
for (size_t i = 0; i < tacke.size(); i++) {
// razmatramo sve tacke osim onih kojima je odredjena poslednja duz
if (i == tekuca || i == naredna)
continue;
Orijentacija o = orijentacija(tacke[tekuca], tacke[naredna], tacke[i]);
if (o == POZITIVNA ||
(o == KOLINEARNE &&
izmedju(tacke[tekuca], tacke[naredna], tacke[i])))
naredna = i;
}
tekuca = naredna;
} while (tekuca != prva);
return omotac;
}# include <iostream> {.unnumbered .unlisted}
# include <vector> {.unnumbered .unlisted}
# include <algorithm> {.unnumbered .unlisted}
using namespace std;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
int x, y;
};
enum Orijentacija { POZITIVNA, NEGATIVNA, KOLINEARNE };
Orijentacija orijentacija(const Tacka& t0, const Tacka& t1, const Tacka& t2) {
long long d = (long long)(t1.x-t0.x)*(long long)(t2.y-t0.y) -
(long long)(t2.x-t0.x)*(long long)(t1.y-t0.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
bool izmedju1(int a, int b, int c) {
return (a <= b && b <= c) || (a >= b && b >= c);
}
bool izmedju(const Tacka& t1, const Tacka& t2, const Tacka& t3) {
return izmedju1(t1.x, t2.x, t3.x) && izmedju1(t1.y, t2.y, t3.y);
}
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// odredjujemo redni broj ekstremne tacke (one sa najmanjom x koordinatom)
auto cmp = [] (const Tacka& t1, const Tacka& t2) {
return t1.x < t2.x || (t1.x == t2.x && t1.y < t2.y);
};
int prva = distance(begin(tacke),
min_element(begin(tacke), end(tacke), cmp));
// niz tacaka koje cine omotac
vector<Tacka> omotac;
// krecemo od ekstremne tacke
int tekuca = prva;
do {
omotac.push_back(tacke[tekuca]);
// krecemo obradu od prve tacke u nizu, osim ako je prva tacka
// bas ekstremna; u tom slucaju krecemo od druge tacke
int naredna = tekuca == 0 ? 1 : 0;
// odredjujemo narednu tacku u omotacu, zahtevajuci da se sve
// ostale tacke nalaze sa desne strane prave odredjene tekucom i
// tom narednom tackom
for (size_t i = 0; i < tacke.size(); i++) {
// razmatramo sve tacke osim onih kojima je odredjena poslednja duz
if (i == tekuca || i == naredna)
continue;
Orijentacija o = orijentacija(tacke[tekuca], tacke[naredna], tacke[i]);
if (o == POZITIVNA ||
(o == KOLINEARNE &&
izmedju(tacke[tekuca], tacke[naredna], tacke[i])))
naredna = i;
}
tekuca = naredna;
} while (tekuca != prva);
return omotac;
}
int main() {
int n;
cin >> n;
vector<Tacka> tacke(n);
for (int i = 0; i < n; i++)
cin >> tacke[i].x >> tacke[i].y;
vector<Tacka> omotac = konveksniOmotac(tacke);
cout << omotac.size() << endl;
for (const Tacka& t : omotac)
cout << t.x << " " << t.y << endl;
return 0;
}Ako je \(m\) broj temena konačnog konveksnog omotača, vremenska složenost uvijanja poklona je \(O(mn)\). Dakle, ovaj algoritam spada u grupu algoritama čija složenost zavisi ne samo od dimenzije ulaza, već i od dimenzije izlaza, tj. algoritama sa izlazno zavisnom složenošću. U slučaju kada je konveksni omotač skupa tačaka trougao (slika 2 desno), algoritam uvijanja poklona ima složenost \(O(n)\), a u slučaju kada sve tačke (ili u opštem slučaju \(O(n)\) tačaka) pripadaju konveksnom omotaču (slika 2 levo) složenost algoritma je \(O(n^2)\).
U nastavku ćemo razmotriti efikasnije algoritme za nalaženje konveksnog omotača.
Krenimo od Grejemovog2 algoritma. Započinje se sortiranjem tačaka prema uglovima, slično kao pri konstrukciji prostog mnogougla. Neka je \(P_0\) ekstremna tačka, recimo ona sa najvećom \(x\)-koordinatom (i sa najmanjom \(y\)-koordinatom, ako ima više tačaka sa najvećom \(x\)-koordinatom). Za svaku tačku \(P_i\) iz datog skupa tačaka izračunavamo ugao između poluprave \(P_0P_i\) i horizontalne poluprave iz \(P_0\) koja se prostire u pravcu pozitivnog smera \(x\)-ose, i sortiramo tačke prema veličini ovih uglova (videti primer na slici ??). Tačke koje zahvataju isti ugao sortiramo na osnovu rastojanja od \(P_0\), opadajuće (tako da se prvo obrađuju dalje tačke). Alternativno, moguće je i da izbacimo sve kolinearne tačke osim one koja je najdalja od \(P_0\).
Tačke, dakle, obilazimo redosledom kojim se pojavljuju u (prostom) mnogouglu, i prilikom obilaska pokušavamo da identifikujemo temena konveksnog omotača. Kao i kod uvijanja poklona pamtimo put sastavljen od tačaka koje su obrađene tokom obilaska. Preciznije, to je konveksni put koji određuje konveksni mnogougao (dobijen povezivanjem prve i poslednje tačke puta), koji sadrži sve do sada pregledane tačke. Zbog toga, je u trenutku kad su sve tačke pregledane, konveksni omotač skupa tačaka konstruisan. Osnovna razlika između ovog algoritma i algoritma uvijanja poklona je u činjenici da tekući konveksni put ne mora da bude deo konačnog konveksnog omotača. On određuje konveksni omotač do sada pregledanih tačaka. Dakle tekući konveksni put može da sadrži tačke koje ne pripadaju konačnom konveksnom omotaču; te tačke biće eliminisane kasnije. Na primer, put od \(P_0\) do \(Q_m\) na slici 5 je konveksan, ali tačke \(Q_m\) i \(Q_{m-1}\) očigledno ne pripadaju konveksnom omotaču kompletnog skupa tačaka. Ovo razmatranje sugeriše algoritam zasnovan na sledećoj induktivnoj hipotezi.
Induktivna hipoteza. Ako je dato \(n\) tačaka u ravni, uređenih prema algoritmu za konstrukciju prostog mnogougla, onda umemo da konstruišemo konveksni put preko nekih od prvih \(k\) tačaka, takav da je njemu odgovarajući konveksni mnogougao konveksni omotač prvih \(k\) tačaka.
Slučaj \(k=1\) je trivijalan (omotač sadrži samo tačku \(P_0\)). Označimo konveksni put dobijen (induktivno) za prvih \(k\) tačaka sa \(P=Q_0, Q_1, \ldots, Q_m\) (pri čemu je \(\{Q_0, \ldots Q_m\} \subseteq \{P_0, \ldots, P_{k-1}\})\). Proširimo induktivnu hipotezu na \(k+1\) tačaka. Posmatrajmo ugao između pravih \(Q_{m-1}Q_m\) i \(Q_{m}P_{k}\) (videti sliku 5).

Ako je taj ugao manji od \(\pi\) (pri čemu se ugao meri iz unutrašnjosti mnogougla), onda se tačka \(P_{k}\) može dodati postojećem putu (novi put je zbog toga takođe konveksan), čime je korak indukcije završen. U protivnom, tvrdimo da tačka \(Q_m\) leži u mnogouglu dobijenom zamenom tačke \(Q_m\) u putu \(P\) tačkom \(P_{k}\), i povezivanjem tačke \(P_{k}\) sa tačkom \(P_0\). Ovo je tačno jer su tačke uređene prema odgovarajućim uglovima, pa se prava \(P_0P_{k}\) nalazi “levo” od prvih \(k\) tačaka. Zbog toga \(Q_m\) jeste unutar gore definisanog mnogougla, može se izbaciti iz puta \(P\), a tačka \(P_{k}\) se može dodati tekućem putu. Da li je time završena obrada \((k+1)\)-ve tačke? Ne mora biti. Nakon izbacivanja tačke \(Q_m\) dobijeni put još ne mora da bude konveksan. Zaista, slika 5 pokazuje da postoje slučajevi kad treba eliminisati još tačaka. Naime, i tačka \(Q_{m-1}\) može da bude unutar mnogougla definisanog modifikovanim putem. Moramo da (unazad) nastavimo sa proverama poslednje dve stranice puta, sve dok ugao između njih ne postane manji od \(\pi\): ovo se uvek mora desiti pre nego što se iscrpu sve tačke, jer će u najgorem slučaju barem tačke \(Q_0\), \(Q_1\) i \(P_k\) činiti konveksni put (zbog prethodnog uređenja tačaka). Put je tada konveksan, a hipoteza je proširena na \(k+1\) tačaka.
Umesto da računamo ugao između pravih \(Q_{m-1}Q_m\) i \(Q_{m}P_{k}\), može se razmatrati orijentacija trojke \(Q_{m-1}Q_mP_k\): ukoliko je orijentacija ovog trougla pozitivna, onda je ugao \(Q_{m-1}Q_mP_k\) manji od \(\pi\), a ako je negativna, taj ugao je veći od \(\pi\). Ako je orijentacija jednaka nuli, tačke \(P_kQ_mQ_{m-1}\) su kolinearne. Na osnovu sortiranja tačaka znamo da tačka \(Q_m\) leži između \(Q_{m-1}\) i \(P_k\), pa se i u tom slučaju \(Q_m\) može zameniti tačkom \(P_k\).
Na slici 6 prikazani su koraci prilikom izvršavanja Grejemovog algoritma na jednom primeru.

U narednom apletu možete videti kako funkcioniše ovaj algoritam. Pronalazi se prvo ekstremna tačka i zatim se tačke, a zatim se obrađuje jedna po jedna (što je prikazano kroz animaciju).
Grejemov algoritam je moguće implementirati na sledeći način:
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// trazimo ekstremnu tacku sa maksimalnom x koordinatom,
// u slucaju da ima vise tacaka sa maksimalnom x koordinatom
// biramo onu sa najmanjom y koordinatom
auto max = max_element(begin(tacke), end(tacke),
[](const Tacka& t1, const Tacka& t2) {
return t1.x < t2.x ||
(t1.x == t2.x && t1.y > t2.y);
});
// dovodimo je na početak niza
swap(*begin(tacke), *max);
const Tacka& t0 = tacke[0];
// sortiramo ostatak niza (tačke sortiramo na osnovu ugla koji
// zaklapaju u odnosu horizontalnu polupravu koja polazi nadesno
// iz ekstremne tacke), a kolinearne na osnovu rastojanja te tacke
sort(next(begin(tacke)), end(tacke),
[t0](const Tacka& t1, const Tacka& t2) {
Orijentacija o = orijentacija(t0, t1, t2);
if (o == KOLINEARNE)
return kvadratRastojanja(t0, t1) <= kvadratRastojanja(t0, t2);
return o == POZITIVNA;
});
// obradjujemo tacke u sortiranom redosledu izbacujuci prethodne sve
// dok se tekuca tacka sa dve poslednje ne cini levi zaokret
vector<Tacka> omotac;
omotac.push_back(tacke[0]);
omotac.push_back(tacke[1]);
for (size_t i = 2; i < tacke.size(); i++) {
while (omotac.size() >= 2 &&
orijentacija(omotac[omotac.size()-2],
omotac[omotac.size()-1],
tacke[i]) != POZITIVNA)
omotac.pop_back();
omotac.push_back(tacke[i]);
}
return omotac;
}# include <iostream> {.unnumbered .unlisted}
# include <vector> {.unnumbered .unlisted}
# include <algorithm> {.unnumbered .unlisted}
using namespace std;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
int x, y;
};
enum Orijentacija { POZITIVNA, NEGATIVNA, KOLINEARNE };
Orijentacija orijentacija(const Tacka& t0, const Tacka& t1, const Tacka& t2) {
long long d = (long long)(t1.x-t0.x)*(long long)(t2.y-t0.y) -
(long long)(t2.x-t0.x)*(long long)(t1.y-t0.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
long long kvadratRastojanja(const Tacka& t1, const Tacka& t2) {
long long dx = t1.x - t2.x, dy = t1.y - t2.y;
return dx*dx + dy*dy;
}
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// trazimo ekstremnu tacku sa maksimalnom x koordinatom,
// u slucaju da ima vise tacaka sa maksimalnom x koordinatom
// biramo onu sa najmanjom y koordinatom
auto max = max_element(begin(tacke), end(tacke),
[](const Tacka& t1, const Tacka& t2) {
return t1.x < t2.x ||
(t1.x == t2.x && t1.y > t2.y);
});
// dovodimo je na početak niza
swap(*begin(tacke), *max);
const Tacka& t0 = tacke[0];
// sortiramo ostatak niza (tačke sortiramo na osnovu ugla koji
// zaklapaju u odnosu horizontalnu polupravu koja polazi nadesno
// iz ekstremne tacke), a kolinearne na osnovu rastojanja te tacke
sort(next(begin(tacke)), end(tacke),
[t0](const Tacka& t1, const Tacka& t2) {
Orijentacija o = orijentacija(t0, t1, t2);
if (o == KOLINEARNE)
return kvadratRastojanja(t0, t1) <= kvadratRastojanja(t0, t2);
return o == POZITIVNA;
});
// obradjujemo tacke u sortiranom redosledu izbacujuci prethodne sve
// dok se tekuca tacka sa dve poslednje ne cini levi zaokret
vector<Tacka> omotac;
omotac.push_back(tacke[0]);
omotac.push_back(tacke[1]);
for (size_t i = 2; i < tacke.size(); i++) {
while (omotac.size() >= 2 &&
orijentacija(omotac[omotac.size()-2],
omotac[omotac.size()-1],
tacke[i]) != POZITIVNA)
omotac.pop_back();
omotac.push_back(tacke[i]);
}
return omotac;
}
int main() {
int n;
cin >> n;
vector<Tacka> tacke(n);
for (int i = 0; i < n; i++)
cin >> tacke[i].x >> tacke[i].y;
vector<Tacka> omotac = konveksniOmotac(tacke);
cout << omotac.size() << endl;
for (const Tacka& t : omotac)
cout << t.x << " " << t.y << endl;
return 0;
}Glavni deo složenosti Grejemovog algoritma potiče od početnog sortiranja. Ostatak algoritma izvršava se za vreme \(O(n)\). Svaka tačka skupa razmatra se tačno jednom u induktivnom koraku kao \(P_{k}\). U tom trenutku tačka se uvek dodaje konveksnom putu. Ista tačka biće razmatrana i kasnije (možda čak i više nego jednom) da bi se proverila njena pripadnost konveksnom putu. Broj tačaka na koje se primenjuje ovakav povratni test može biti veliki, ali se sve one, sem dve (tekuća tačka i tačka za koju se ispostavlja da dalje pripada konveksnom putu) eliminišu, a tačka može biti eliminisana samo jednom! Prema tome, troši se najviše konstantno vreme za eliminaciju svake tačke i konstantno vreme za njeno dodavanje, te je ukupna složenost ove faze \(O(n)\). Zbog početnog sortiranja tačaka vreme izvršavanja kompletnog algoritma iznosi \(O(n\log n)\).
Pokušajmo da isti problem rešimo tehnikom dekompozicije, nalik algoritmu brzog sortiranja (engl. QuickSort). Odredimo tačke iz datog skupa sa minimalnom i maksimalnom \(x\) koordinatom (ako ima više takvih onda biramo onu sa minimalnom ili maksimalnom \(y\) koordinatom): neka su to tačke \(P_i\) i \(P_j\). Obe ove tačke su ekstremne i kao takve sigurno pripadaju konveksnom omotaču. Duž \(P_iP_j\) deli skup tačaka na dva podskupa: svaki od podskupova čine tačke koje se nalaze sa iste strane te duži. Razmotrimo jedan od ova dva podskupa: u njemu tražimo tačku na maksimalnom rastojanju od duži \(P_iP_j\): neka je to tačka \(P_k\) (slika 7). I ona sigurno pripada konveksnom omotaču. Tačke iz skupa koje pripadaju zatvorenom trouglu \(P_iP_jP_k\) ne mogu biti deo konveksnog omotača i ne moraju se dalje razmatrati. Prethodno razmatranje sada možemo primeniti na dve nove duži koje formiraju trougao: \(P_iP_k\) i \(P_kP_j\): tražimo najudaljeniju tačku od duži \(P_iP_k\) sa one strane prave \(P_iP_k\) sa koje nije \(P_j\) i, slično, najudaljeniju tačku od duži \(P_kP_j\) sa one strane prave \(P_kP_j\) sa koje nije tačka \(P_i\). Sa postupkom nastavljamo sve dok na raspolaganju ima još tačaka. Tačke koje su tokom izvršavanja algoritma birane kao najudaljenije pripadaju konveksnom omotaču. Na ovaj način došli smo do tzv. brzog algoritma za određivanje konveksnog omotača (engl. QuickHull algorithm).
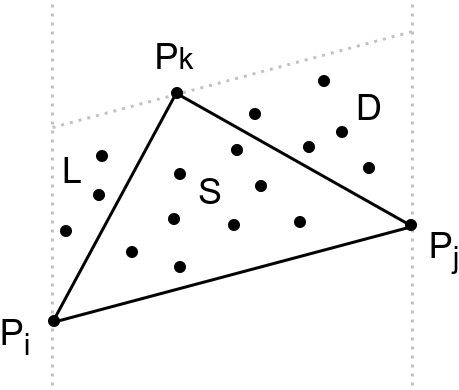
Napomenimo da prilikom traženja najudaljenije tačke \(P_k\) od duži \(P_iP_j\), nije neophodno računati tačno rastojanje po formuli:
\[d=\frac{|\vek{P_kP_i}\times \vek{P_kP_j}|}{|\vek{P_iP_j}|}\]
Naime, mi tražimo najudaljeniju tačku od prave kroz fiksirane dve tačke, te će imenilac ovog razlomka uvek biti isti. Stoga se mera rastojanja ovde može računati po formuli \(d=|\vek{P_kP_i}\times \vek{P_kP_j}|\).
U narednom apletu možete videti kako funkcioniše ovaj algoritam. U svakom koraku je prikazana duž koja se obrađuje. Ako postoji tačka koja je najudaljenija od nje ona se boji u crveno i prikazuje se trougao koji gradi duž i ta tačka.
U nastavku je prikazana C++ implementacija ovog algoritma. Tokom rekurzivnih poziva održava se skup temena konveksnog omotača. Na kraju je potrebno odrediti i redosled tih temena, tako da uzastopna temena jedinstvenog konveksnog mnogougla budu jedno iza drugog. To se može postići tako što se neka ekstremna tačka \(T_0\), u ovom slučaju ona sa maksimalnom \(x\)-koordinatom, stavi na početak, a zatim se ostale tačke \(T_i\) sortiraju po uglu koji poluprava \(T_0T_i\) zaklapa sa horizontalnom polupravom koja počinje u \(T_0\) i prostire se u pravcu pozitivnog dela \(x\)-ose. Zaista, u traženom konveksnom mnogouglu tačke su sortirane na taj način, pa se ovim sortiranjem dobija baš taj konveksan mnogougao (koji je jedinstven). Pošto je osnovni algoritam takav da je moguće da su u izgrađenom omotaču neka tri temena kolinearna, nakon formiranja omotača vršimo njegovo uprošćavanje zadržavajući samo krajnja temena u nizu kolinearnih temena.
// funkcija koja racuna konveksni omotac skupa tacaka
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// funkcija poredjenja koja je potrebna za bibliotecke funkcije
// min_element i max_element
auto porediKoordinate =
[](const Tacka& A, const Tacka& B) {
return (A.x < B.x) || (A.x == B.x && A.y > B.y);
};
// trazimo tacke sa najmanjom i najvecom x koordinatom
int min = distance(tacke.begin(),
min_element(tacke.begin(), tacke.end(),
porediKoordinate));
int max = distance(tacke.begin(),
max_element(tacke.begin(), tacke.end(),
porediKoordinate));
// skup temena omotaca
set<Tacka> temena;
// rekurzivno trazimo konveksne omotace tacaka sa jedne strane
// duzi odredjene tackama tacka[min] i tacka[max]
vector<Tacka> iznad =
izdvojOrijentaciju(tacke, tacke[min], tacke[max], POZITIVNA);
konveksniPoluomotac(iznad, tacke[min], tacke[max], temena);
// i sa druge strane
vector<Tacka> ispod =
izdvojOrijentaciju(tacke, tacke[min], tacke[max], NEGATIVNA);
konveksniPoluomotac(ispod, tacke[min], tacke[max], temena);
// prebacujemo tacke iz skupa u vektor i soritramo ga po uglovima
vector<Tacka> omotac(temena.begin(), temena.end());
const Tacka& maxTacka = tacke[max];
auto porediUgao =
[maxTacka](const Tacka& A, const Tacka& B) {
if (A == maxTacka) return true;
if (B == maxTacka) return false;
return orijentacija(maxTacka, A, B) == POZITIVNA;
};
sort(begin(omotac), end(omotac), porediUgao);
// eliminisemo susedne kolinearne tacke
vector<Tacka> omotacBezKolinearnih;
for (int i = 0; i < omotac.size(); i++) {
int prethodna = i == 0 ? omotac.size() - 1 : i-1;
int sledeca = i == omotac.size() - 1 ? 0 : i + 1;
if (orijentacija(omotac[prethodna], omotac[i], omotac[sledeca]) !=
KOLINEARNE)
omotacBezKolinearnih.push_back(omotac[i]);
}
return omotacBezKolinearnih;
}
void konveksniPoluomotac(const vector<Tacka>& tacke,
const Tacka& P, const Tacka& Q,
set<Tacka>& temena) {
// dodajemo tacke P i Q u omotac
temena.insert(P);
temena.insert(Q);
// ako ne postoji tacka sa date strane prave PQ zavrsavamo postupak
if (tacke.empty())
return;
// trazimo tacku sa date strane duzi PQ
// koja je na najvecem rastojanju od prave PQ
// pozicija najdalje tacke i njeno rastojanje od prave PQ
int iMax = -1; long long dMax = 0;
for (int i = 0; i < tacke.size(); i++) {
long long di = rastojanjeOdPrave(P, Q, tacke[i]);
if (di > dMax) {
iMax = i;
dMax = di;
}
}
// najdalja tacka
const Tacka& M = tacke[iMax];
// rekurzivno pozivamo za dva podskupa dobijena tackom `tacke[iMax]`
// analiziramo tacke koje su na suprotnoj strani prave MP u odnosu na Q
vector<Tacka> suprotnoOdQ =
izdvojOrijentaciju(tacke, M, P, -orijentacija(M, P, Q));
konveksniPoluomotac(suprotnoOdQ, M, P, temena);
// analiziramo tacke koje su na suprotnoj strani prave MQ u odnosu na P
vector<Tacka> suprotnoOdP =
izdvojOrijentaciju(tacke, M, Q, -orijentacija(M, Q, P));
konveksniPoluomotac(suprotnoOdP, M, Q, temena);
}
// funkcija koja vraca vrednost koja je proporcionalna rastojanju
// od tacke A do prave odredjene tackama P i Q
long long rastojanjeOdPrave(Tacka P, Tacka Q, Tacka A) {
return abs((long long)(A.y - P.y) * (long long)(Q.x - P.x) -
(long long)(Q.y - P.y) * (long long)(A.x - P.x));
}
vector<Tacka> izdvojOrijentaciju(const vector<Tacka>& tacke,
const Tacka& P, const Tacka& Q,
int o) {
vector<Tacka> rezultat;
for (const Tacka& T : tacke)
if (orijentacija(P, Q, T) == o)
rezultat.push_back(T);
return rezultat;
}# include <iostream> {.unnumbered .unlisted}
# include <vector> {.unnumbered .unlisted}
# include <set> {.unnumbered .unlisted}
# include <algorithm> {.unnumbered .unlisted}
using namespace std;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
int x, y;
bool operator==(const Tacka& druga) const {
return x == druga.x && y == druga.y;
}
};
// posto cemo konveksni omotac pamtiti u vidu skupa tacaka
// neophodno je da definisemo operator < za dve tacke
bool operator<(const Tacka& A, const Tacka&B){
return A.x < B.x || (A.x == B.x && A.y < B.y);
}
// racuna se kvadrat rastojanja izmedju tacaka A i B
long long kvadratRastojanja(Tacka A, Tacka B) {
long long dx = A.x - B.x, dy = A.y - B.y;
return dx*dx + dy*dy;
}
enum Orijentacija { POZITIVNA=1, NEGATIVNA=-1, KOLINEARNE=0 };
// orijentacija uredjene trojke tacaka P,Q i R
int orijentacija(Tacka P, Tacka Q, Tacka R){
long long d = (long long)(Q.y - P.y) * (long long)(R.x - Q.x) -
(long long)(Q.x - P.x) * (long long)(R.y - Q.y);
if (d == 0)
return KOLINEARNE;
else if (d > 0)
return NEGATIVNA;
else
return POZITIVNA;
}
// funkcija koja vraca vrednost koja je proporcionalna rastojanju
// od tacke A do prave odredjene tackama P i Q
long long rastojanjeOdPrave(Tacka P, Tacka Q, Tacka A) {
return abs((long long)(A.y - P.y) * (long long)(Q.x - P.x) -
(long long)(Q.y - P.y) * (long long)(A.x - P.x));
}
// izdvaja sve tacke T iz vektora tacke takve da je orijentacija P Q T
// jednaka o
vector<Tacka> izdvojOrijentaciju(const vector<Tacka>& tacke,
const Tacka& P, const Tacka& Q,
int o) {
vector<Tacka> rezultat;
for (const Tacka& T : tacke)
if (orijentacija(P, Q, T) == o)
rezultat.push_back(T);
return rezultat;
}
// trazimo konveksni omotac tacaka sa jedne strane duzi PQ
// i dodajemo ih u skup temena konveksnog omotaca
void konveksniPoluomotac(const vector<Tacka>& tacke,
const Tacka& P, const Tacka& Q,
set<Tacka>& temena) {
// dodajemo tacke P i Q u omotac
temena.insert(P);
temena.insert(Q);
// ako ne postoji tacka sa date strane prave PQ zavrsavamo postupak
if (tacke.empty())
return;
// trazimo tacku sa date strane duzi PQ
// koja je na najvecem rastojanju od prave PQ
// pozicija najdalje tacke i njeno rastojanje od prave PQ
int iMax = -1; long long dMax = 0;
for (int i = 0; i < tacke.size(); i++) {
long long di = rastojanjeOdPrave(P, Q, tacke[i]);
if (di > dMax) {
iMax = i;
dMax = di;
}
}
// najdalja tacka
const Tacka& M = tacke[iMax];
// rekurzivno pozivamo za dva podskupa dobijena tackom `tacke[iMax]`
// analiziramo tacke koje su na suprotnoj strani prave MP u odnosu na Q
vector<Tacka> suprotnoOdQ =
izdvojOrijentaciju(tacke, M, P, -orijentacija(M, P, Q));
konveksniPoluomotac(suprotnoOdQ, M, P, temena);
// analiziramo tacke koje su na suprotnoj strani prave MQ u odnosu na P
vector<Tacka> suprotnoOdP =
izdvojOrijentaciju(tacke, M, Q, -orijentacija(M, Q, P));
konveksniPoluomotac(suprotnoOdP, M, Q, temena);
}
// funkcija koja racuna konveksni omotac skupa tacaka
vector<Tacka> konveksniOmotac(vector<Tacka>& tacke) {
// funkcija poredjenja koja je potrebna za bibliotecke funkcije
// min_element i max_element
auto porediKoordinate =
[](const Tacka& A, const Tacka& B) {
return (A.x < B.x) || (A.x == B.x && A.y > B.y);
};
// trazimo tacke sa najmanjom i najvecom x koordinatom
int min = distance(tacke.begin(),
min_element(tacke.begin(), tacke.end(),
porediKoordinate));
int max = distance(tacke.begin(),
max_element(tacke.begin(), tacke.end(),
porediKoordinate));
// skup temena omotaca
set<Tacka> temena;
// rekurzivno trazimo konveksne omotace tacaka sa jedne strane
// duzi odredjene tackama tacka[min] i tacka[max]
vector<Tacka> iznad =
izdvojOrijentaciju(tacke, tacke[min], tacke[max], POZITIVNA);
konveksniPoluomotac(iznad, tacke[min], tacke[max], temena);
// i sa druge strane
vector<Tacka> ispod =
izdvojOrijentaciju(tacke, tacke[min], tacke[max], NEGATIVNA);
konveksniPoluomotac(ispod, tacke[min], tacke[max], temena);
// prebacujemo tacke iz skupa u vektor i soritramo ga po uglovima
vector<Tacka> omotac(temena.begin(), temena.end());
const Tacka& maxTacka = tacke[max];
auto porediUgao =
[maxTacka](const Tacka& A, const Tacka& B) {
if (A == maxTacka) return true;
if (B == maxTacka) return false;
return orijentacija(maxTacka, A, B) == POZITIVNA;
};
sort(begin(omotac), end(omotac), porediUgao);
// eliminisemo susedne kolinearne tacke
vector<Tacka> omotacBezKolinearnih;
for (int i = 0; i < omotac.size(); i++) {
int prethodna = i == 0 ? omotac.size() - 1 : i-1;
int sledeca = i == omotac.size() - 1 ? 0 : i + 1;
if (orijentacija(omotac[prethodna], omotac[i], omotac[sledeca]) !=
KOLINEARNE)
omotacBezKolinearnih.push_back(omotac[i]);
}
return omotacBezKolinearnih;
}
int main() {
int n;
cin >> n;
vector<Tacka> tacke(n);
for (int i = 0; i < n; i++)
cin >> tacke[i].x >> tacke[i].y;
vector<Tacka> omotac = konveksniOmotac(tacke);
cout << omotac.size() << endl;
for (const Tacka& t : omotac)
cout << t.x << " " << t.y << endl;
return 0;
}Složenost ovog algoritma može se opisati rekurentnom jednačinom oblika \(T(n)=T(k)+T(n-k-1)+O(n)\), gde je sa \(k\) označena veličina jednog, a sa \(n-k-1\) veličina drugog problema na koji se vrši podela (nalik algoritmu QuickSort). U najboljem slučaju problem se uvek deli na dva potproblema iste dimenzije pa dobijamo rekurentnu jednačinu \(T(n)=2T(n/2)+O(n)\), čije je rešenje \(T(n)=O(n\log n)\). U najgorem slučaju dobijamo rekurentnu jednačinu oblika \(T(n)=T(n-1)+O(n)\) čije rešenje zadovoljava jednačinu \(T(n)=O(n^2)\). Ovo odgovara složenosti algoritma QuickSort i moguće je dokazati da je prosečna složenost ovog algoritma jednaka \(O(n \log{n})\).