
U mnogim primenama je potrebno da se ispita da li tačka sa datim koordinatama pripada unutrašnjosti mnogougla koji ograničava neku oblast. Na primer, u aplikacijama sa grafičkim korisničkim interfejsom ili računarskim igrama je potrebno odrediti da li se pokazivač miša nalazi unutar nekog objekta, koji je predstavljen mnogouglom. Još jedna primena je u sklopu geokodiranja. Zadatak geokodiranja jeste proces koji za zadato mesto ili adresu vraća njegove geografske koordinate. Jednako važan zadatak je i njemu inverzan, kojim se za date koordinate određuje mesto – grad, država ili neka oblast kojoj tačka sa tim koordinatama pripada.
Rešenje ovog problema se razlikuje u odnosu na to kakav je mnogougao koji se analizira (da li je prost, da li je konveksan i slično).
U poglavlju 32 razmotrili smo na koji način možemo utvrditi da li se tačka nalazi unutar datog trougla. Razmotrimo kako se ovo može uopštiti na proizvoljni prost mnogougao.
Problem. Zadat je prost mnogougao \(P_1\ldots P_n\) i tačka \(Q\), koja ne leži na nekoj od njegovih stranica. Ustanoviti da li je tačka \(Q\) unutar tog mnogougla.
Primetimo da smo, jednostavnosti radi, izostavili pitanje provere da li se tačka nalazi na stranicama prostog mnogougla, pa nije relevantno da li se radi o otvorenom ili zatvorenom mnogouglu.

Problem na prvi pogled izgleda jednostavno, ali ako se razmatraju složeni nekonveksni mnogouglovi, kao onaj prikazan na slici 1, vidi se da to nije uvek slučaj. Intuitivni pristup je pokušati nekako “izaći napolje”, polazeći od zadate tačke \(Q\). Posmatrajmo proizvoljnu polupravu sa temenom \(Q\). Vidi se da je dovoljno prebrojati preseke sa stranicama mnogougla. U primeru na slici 1, idući na severoistok1 od date tačke (prateći isprekidanu liniju), nailazimo na šest preseka sa mnogouglom. Pošto nas poslednji presek pre izlaska izvodi iz unutrašnjosti mnogougla, a pretposlednji nas vraća u njegovu unutrašnjost, i tako dalje, tačka \(Q\) je u spoljašnjosti mnogougla. Dakle, možemo zaključiti da tačka \(Q\) pripada unutrašnjosti mnogougla ako i samo ako je broj preseka poluprave iz \(Q\) sa stranicama mnogougla neparan.
Razmotrimo kako se ovaj algoritam može implementirati ako je mnogougao zadat nizom koordinata temena, što je uobičajeni scenario. Kada se problem rešava vizuelno, lako je naći dobar put (polupravu sa malo preseka) i nije potrebno razmatrati stranice mnogougla koje su daleko od tog puta. U slučaju mnogougla datog nizom koordinata, to nije jednostavno i najveći deo vremena troši se na ispitivanje postojanja preseka poluprave i stranica mnogougla, jer nema jednostavnog načina da se izbegne obrada svih stranica. Ispitivanje preseka duži (stranice mnogougla) i poluprave se može uprostiti ako je poluprava koja sadrži tačku \(Q\) paralelna jednoj od osa — na primer \(y\)-osi i recimo usmerena nadole (kao na slici 2). Označimo tu polupravu sa \(q\).

Naime, presek poluprave \(q\) sa stranicom \(P_iP_{i+1}\) mnogougla postoji ako se \(x\)-koordinata tačke \(Q\) nalazi između vrednosti \(x\)-koordinata temena \(P_i\) i \(P_{i+1}\) i ako je \(y\)-koordinata presečne tačke poluprave \(q\) i prave \(P_iP_{i+1}\) manja od \(y\)-koordinate tačke \(Q\). Pretpostavimo, jednostavnosti radi, da je \(x_{P_i} < x_{P_{i+1}}\) (ako nije, možemo razmeniti te dve tačke). Presečna tačka prave \(x=x_Q\) i prave \(P_iP_{i+1}\) čija je jednačina \(y-y_{P_i}=\frac{y_{P_{i+1}}-y_{P_i}}{x_{P_{i+1}}-x_{P_i}}(x-x_{P_i})\) je tačka čija je \(x\)-koordinata \(x_Q\), a \(y\)-koordinata je jednaka:
\[y=y_{P_i}+\frac{y_{P_{i+1}}-y_{P_i}}{x_{P_{i+1}}-x_{P_i}}(x_Q-x_{P_i}).\]
Dakle, potrebno je da važi \(y \leq y_Q\), što se, kada se izraz transformiše da bi se izbeglo deljenje (imenilac razlomka je pozitivan), svodi na:
\[y_{P_i}(x_{P_{i+1}}-x_{P_i}) + (y_{P_{i+1}}-y_{P_i})(x_Q-x_{P_i}) \leq y_Q(x_{P_{i+1}}-x_{P_i})\]
tj. \[(y_{P_i} - y_Q)(x_{P_{i+1}}-x_{P_i}) \leq (y_{P_{i+1}}-y_{P_i})(x_{P_i} - x_Q)\]
Do ovog izraza se može doći i ako se proveri orijentacija trojke tačaka \(P_iP_{i+1}Q\) (ta orijentacija je pozitivna ako i samo ako se tačka \(Q\) se nalazi iznad duži \(P_iP_{i+1}\), što je potrebno da bi presek mogao da postoji).
U narednom apletu možete videti kako izlgeda implementacija ovog pristupa.
Kao što je već pomenuto, obično postoje neki specijalni slučajevi koje treba posebno razmotriti. Cilj je utvrditi da li tačka \(Q\) pripada unutrašnjosti mnogougla \(P\) na osnovu broja preseka poluprave \(q\) sa stranicama mnogougla \(P\). Razmotrimo presek poluprave \(q\) i stranice \(P_iP_{i+1}\). Prvi specijalni slučaj je kada poluprava \(q\) sadrži jednu krajnju tačku te stranice (tj. teme \(P_i\) ili \(P_{i+1}\) mnogougla), ali ne sadrži tu celu stranicu. Bez gubitka na opštosti pretpostavimo da \(q\) sadrži teme \(P_i\). Na slici 3 (a) prikazan je slučaj kad taj presek ne treba brojati, a na slici 3 (b) slučaj kad taj presek treba brojati.

Postoji više načina za utvrđivanje da li neki ovakav presek treba brojati ili ne. Navedimo dva.
Ako su dva temena mnogougla susedna temenu \(P_i\) sa iste strane poluprave \(q\) (tj. prave koja je sadrži), presek se ne računa (oba susedna temena na slici 3 (a) su sa leve strane poluprave \(q\)). U protivnom, ako su temena susedna temenu \(P_i\) sa različitih strana ove prave, presek se broji (na 3 (b) jedno susedno teme je sa leve, a drugo sa desne poluprave \(q\)).
S obzirom na to da razmatramo pravu koja je paralelna sa \(y\)-osom, za svaku stranicu mnogougla trebalo bi računati preseke sa levim temenom, a ne sa desnim (temena neke stranice mnogougla klasifikujemo kao levo i desno u odnosu na vrednosti \(x\)-koordinate temena). Na taj način nećemo računati presek nalik onom na slici 3 (a) jer je za obe stranice mnogougla susedne temenu \(P_i\) presek kroz desno teme (i slično dva puta bismo računali presek sa temenom koje je levi ekstremum i opet se ne bi promenila parnost brojača). Za presek prikazan na slici 3 (b) ubrajamo jedan presek, jer je za jednu od stranica koje se sustiču u tom temenu to levo teme, a za drugu desno.
Drugi specijalan slučaj se javlja kada poluprava \(q\) sadrži stranicu \(P_iP_{i+1}\). Na slici 3 (c) prikazan je slučaj kad taj presek ne treba brojati, a na slici 3 (d) slučaj kad taj presek treba brojati.
Jedan način da se odredi da li presek treba ili ne treba brojati je da se proveri da li su temena susedna stranici \(P_iP_{i+1}\) (temena \(P_{i-1}\) i \(P_{i+2}\)) sa iste ili sa raznih strana poluprave \(q\).
U pristupu u kom se za svaku stranicu broje samo preseci sa levim temenom, a ne i sa desnim, preseke sa vertikalnim dužima treba prosto zanemariti. Zaista, na slici 3
U nastavku ćemo razmotriti implementaciju algoritma za ispitivanje da li je tačka u unutrašnjosti mnogougla koja ne uključuje obradu specijalnih slučajeva.
// utvrdjuje da li se tacka Q nalazi u datom prostom mnogouglu P
// (on je zadat nizom svojih temena, kojih ima bar 3)
bool tackaUMnogouglu(const vector<Tacka>& P, const Tacka& Q) {
// broj temena
int n = P.size();
// razmatramo preseke stranica sa vertikalnom pravom iz Q
// tacka je inicijalno van mnogougla
bool uMnogouglu = false;
// prolazimo skupom svih stranica mnogougla
for (int i = 0; i < n; i++) {
// naredno teme u poretku temena mnogougla
int j = (i + 1) % n;
// obezbedjujemo da prva tacka ima manju x koordinatu
Tacka Pi = P[i], Pj = P[j];
if (Pi.x > Pj.x) swap(Pi, Pj);
// ako se x koordinata tacke Q nalazi izmedju vrednosti
// x koordinata krajnjih tacaka stranice PiPj i
// y koordinata presecne tacka prave x = x_Q i prave PiPj
// je manja od y koordinate tacke Q
if (Pi.x < Q.x && Q.x < Pj.x &&
(Pi.y-Q.y)*(Pj.x-Pi.x) <= (Pj.y-Pi.y)*(Pi.x-Q.x))
// registrujemo jos jedan presek
uMnogouglu = !uMnogouglu;
}
return uMnogouglu;
} Neka je \(n\) broj stranica mnogougla. Kroz osnovnu petlju algoritma prolazi se \(n\) puta. U svakom prolasku kroz petlju računa se presek dve prave i izvršavaju se još neke operacije za konstantno vreme. Dakle, ukupno vreme izvršavanja algoritma iznosi \(O(n)\). Algoritam se može ubrzati tako što se izbegne analiza nekih stranica mnogougla, što se može učiniti smeštanjem stranica u specijalne strukture podataka koje omogućavaju brzu prostornu pretragu, poput, na primer, \(R\)-drveta (engl. \(R\)-trees), čije izučavanje prepuštamo čitaocu.
Provera pripadnosti tačke unutrašnjosti mnogougla može biti mnogo efikasnija ako je mnogougao konveksan.
Problem. Ispitati da li tačka \(Q\) pripada unutrašnjosti konveksnog mnogougla \(P_0P_1\ldots P_{n-1}\).
Za početak pretpostavimo da tačka \(Q\) ne pripada stranicama datog konveksnog mnogougla \(P_0P_1\ldots P_{n-1}\).
Jedno moguće rešenje je uopštenje algoritma za ispitivanje da li tačka pripada unutrašnjosti datog trougla. Ono nije efikasnije nego opšte rešenje za prost mnogougao, ali je jednostavnije od njega. Jednostavnosti radi, pretpostavimo da su temena konveksnog mnogougla data u matematički pozitivnom smeru (smeru suprotnom od smera kazaljke na časovniku). Tačka \(Q\) pripada unutrašnjosti mnogougla ako i samo ako se nalazi s leve strane svake usmerene stranice \(P_iP_{i+1}\), \(0\leq i\leq n-1, P_n=P_0\) mnogougla, odnosno ako za svako \(i\) trojka tačaka \(P_iP_{i+1}Q\) ima pozitivnu orijentaciju. U primeru prikazanom na slici 4 ovaj uslov važi za tačku \(Q\) na slici levo, ali ne i za tačku \(Q\) na slici desno. Složenost ovog algoritma iznosi \(O(n)\).

U narednom apletu možete videti kako funkcioniše provera da li tačka pripada unutrašnjosti konveksnog mnogougla. Zelenim su označene stranice za koje važi da je orijentacija \(P_iP_{i+1}Q\) pozitivna, žutom one za koje je ta orijentacija nula, a crvenom one za koje je negativna.
Ako nije poznata orijentacija temena konveksnog mnogougla (već samo njihov redosled) kako bi se utvrdilo da li tačka \(Q\) pripada unutrašnjosti mnogougla moguće je proveriti da li svaka trojka \(P_iP_{i+1}Q\) ima istu orijentaciju (bila ona pozitivna ili negativna).
Ako je orijentacija neke trojke \(P_iP_{i+1}Q\) jednaka nuli, to znači da tačka \(Q\) pripada pravoj \(P_iP_{i+1}\), pa pošto smo pretpostavili da \(Q\) ne pripada stranici \(P_iP_{i+1}\), ona sigurno pripada spoljašnjosti mnogougla.
Možemo razmotriti i opštiji problem, u kom nije unapred poznato da tačka ne pripada stranicama mnogougla. Tada, ako je orijentacija neke trojke \(P_iP_{i+1}Q\) jednaka nuli, eksplicitno treba proveriti da li tačka \(Q\) pripada duži \(P_iP_{i+1}\) (što se može uraditi proverom projekcija na ose, kako je opisano u poglavlju 28) i rezultat izračunati u skladu sa tim da li razmatramo otvoren ili zatvoren mnogougao (tj. da li pored unutrašnjosti dopuštamo i pripadnost tačke stranicama mnogougla).
Ideja na kojoj se zasniva efikasniji algoritam se oslanja na binarnu pretragu. Jednostavnije je implementirati proveru da li tačka pripada zatvorenom mnogouglu.
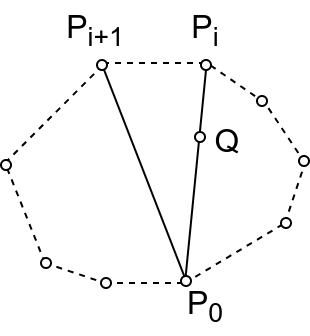
Lema 60. Neka se tačke \(Q\) i \(P_m\) nalaze unutar ugla \(\angle P_iP_0P_j\) (slika 5), pri čemu trojka tačaka \(P_0P_iP_j\) ima pozitivnu orijentaciju. Tada važi:
ako su tačke \(P_i\) i \(Q\) sa iste strane prave \(P_0P_m\), tj. ako su trojke \(P_0P_mP_i\) i \(P_0P_mQ\) isto orijentisane, tada tačka \(Q\) pripada uglu \(\angle P_iP_0P_m\) (tj. njegovoj unutrašnjosti). Ovaj uslov svodi se na to da je trojka tačaka \(P_0P_mQ\) negativno orijentisana.
ako su tačke \(P_j\) i \(Q\) sa iste strane prave \(P_0P_m\) (kao na slici 5), tj. ako su trojke \(P_0P_mP_j\) i \(P_0P_mQ\) isto orijentisane, tada tačka \(Q\) pripada ugla \(\angle P_mP_0P_j\) (tj. njegovoj unutrašnjosti). Ovaj uslov svodi se na to da je trojka tačaka \(P_0P_mQ\) pozitivno orijentisana (što je, naravno, uslov suprotan onom u prethodnom slučaju).
ako tačka \(Q\) baš pripada pravoj \(P_0P_m\), usvajamo dogovor da tačka \(Q\) pripada uglu \(\angle P_iP_0P_m\).

Iskoristićemo prethodnu lemu da binarnom pretragom pronađemo vrednost \(i\) takvu da tačka \(Q\) pripada zatvorenom uglu \(P_iP_0P_{i+1}\). Održavaćemo tekući ugao \(\angle P_iP_0P_j\) kome pripada tačka \(Q\), koji inicijalizujemo na \(\angle P_1P_0P_{n-1}\). U svakom koraku za tačku \(P_m\) biramo središnju tačku – tačku sa indeksom \(m=\lfloor (i+j)/2\rfloor\) i ažuriramo ugao kome pripada tačka \(Q\) prema prethodnoj lemi. Zaustavljamo se kada tačke \(P_i\) i \(P_j\) postanu susedna temena mnogougla, tj. kada je \(j = i+1\). Posle najviše \(O(\log n)\) koraka pronalazi se ugao \(\angle P_iP_0P_{i+1}\) kome tačka \(Q\) mora pripadati ako pripada zatvorenom mnogouglu. Tada znamo da tačka \(Q\) pripada zatvorenom mnogouglu ako i samo ako pripada zatvorenom trouglu \(\bigtriangleup P_0P_iP_{i+1}\). Složenost je, dakle \(O(\log{n})\). Na slici 6 prikazan je primer postupka polovljenja ugla kome pripada tačka \(Q\).

Na početku je moguće proveriti da li tačka pripada uglu \(\angle P_1P_0P_{n-1}\) i ako ne pripada odmah se može zaključiti da tačka ne pripada ni mnogouglu. Međutim, ta provera nije neophodna, jer ako tačka ne pripada tom uglu binarnom pretragom će se doći ili do trougla \(\bigtriangleup P_0P_1P_2\) ili \(\bigtriangleup P_0P_{n-2}P_{n-1}\) i tada će se zaključiti da mu tačka ne pripada, pa ne pripada ni zatvorenom mnogouglu.
U narednom apletu možete videti kako funkcioniše provera pripadnosti konveksnom mnogouglu binarnom pretragom. U svakom koraku poznat je ugao \(\angle P_iP_0P_j\) kome tačka mora pripadati ako pripada mnogouglu. Na kraju se proverava pripadnost trouglu \(\bigtriangleup P_0P_iP_{i+1}\).
Ovaj algoritam se može veoma jednostavno implementirati.
// niz sadrzi redom tacke mnogougla P, funkcija proverava da li se tacka Q
// nalazi unutar preseka zatvorenog mnogougla P i ugla P[l]P[0]P[d]
bool tackaUZatvorenomKonveksnomMnogouglu(const vector<Tacka>& P,
const Tacka& Q, int i, int j) {
if (j - i == 1)
return tackaUZatvorenomTrouglu(Q, P[0], P[i], P[j]);
int m = i + (j - i) / 2;
if (orijentacija(P[0], P[m], Q) == POZITIVNA)
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, m, j);
else
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, i, m);
}
// provera da li dati zatvoreni konveksni mnogougao P sadrzi tacku Q
bool tackaUZatvorenomKonveksnomMnogouglu(const vector<Tacka>& P,
const Tacka& Q) {
int n = P.size();
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, 1, n-1);
}# include <iostream> {.unnumbered .unlisted}
# include <vector> {.unnumbered .unlisted}
# include <utility> {.unnumbered .unlisted}
using namespace std;
typedef pair<int, int> Tacka;
enum Orijentacija {POZITIVNA, NEGATIVNA, KOLINEARNE};
Orijentacija orijentacija(const Tacka& a, const Tacka& b, const Tacka& c) {
int xa = a.first, ya = a.second;
int xb = b.first, yb = b.second;
int xc = c.first, yc = c.second;
long long d = (long long)(xb-xa)*(long long)(yc-ya) -
(long long)(xc-xa)*(long long)(yb-ya);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
bool saIsteStrane(const Tacka& T1, const Tacka& T2,
const Tacka& A1, const Tacka& A2) {
Orijentacija o1 = orijentacija(T1, T2, A1);
Orijentacija o2 = orijentacija(T1, T2, A2);
if (o1 == KOLINEARNE || o2 == KOLINEARNE)
return true;
return o1 == o2;
}
bool tackaUZatvorenomTrouglu(const Tacka& A, const Tacka& T1, const Tacka& T2,
const Tacka& T3) {
return saIsteStrane(T1, T2, T3, A) &&
saIsteStrane(T1, T3, T2, A) &&
saIsteStrane(T2, T3, T1, A);
}
// niz sadrzi redom tacke mnogougla P, funkcija proverava da li se tacka Q
// nalazi unutar preseka zatvorenog mnogougla P i ugla P[l]P[0]P[d]
bool tackaUZatvorenomKonveksnomMnogouglu(const vector<Tacka>& P,
const Tacka& Q, int i, int j) {
if (j - i == 1)
return tackaUZatvorenomTrouglu(Q, P[0], P[i], P[j]);
int m = i + (j - i) / 2;
if (orijentacija(P[0], P[m], Q) == POZITIVNA)
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, m, j);
else
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, i, m);
}
// provera da li dati zatvoreni konveksni mnogougao P sadrzi tacku Q
bool tackaUZatvorenomKonveksnomMnogouglu(const vector<Tacka>& P,
const Tacka& Q) {
int n = P.size();
return tackaUZatvorenomKonveksnomMnogouglu(P, Q, 1, n-1);
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int n;
cin >> n;
vector<Tacka> mnogougao(n);
for (int i = 0; i < n; i++) {
cin >> mnogougao[i].first >> mnogougao[i].second;
}
int m;
cin >> m;
for (int i = 0; i < m; i++) {
Tacka A;
cin >> A.first >> A.second;
if (tackaUZatvorenomKonveksnomMnogouglu(mnogougao, A))
cout << "da" << '\n';
else
cout << "ne" << '\n';
}
return 0;
}Ako razmatramo otvoreni mnogougao, u prvoj fazi na isti način pronalazimo ugao \(P_iP_0P_{i+1}\) kome tačka \(Q\) pripada. Tačka \(Q\) pripada otvorenom mnogouglu ako i samo ako pripada unutrašnjosti trougla \(P_iP_0P_{i+1}\) ili pripada duži \(P_0P_i\) (kada je \(i\neq 1\)) ili pripada duži \(P_0P_{i+1}\) (kada je \(i\neq n-2\)).
Radi jednostavnijeg objašnjenja algoritma, pretpostavljamo da se u Dekartovom koordinatom sistemu zna šta je gore, dole, desno, levo, tj. gde su sever, jug, istok i zapad.↩︎