Pomeranje kontrolnih tačaka

Kako promena pozicija kontrolnih tačaka utiče na promenu oblika njima definisane Bézier-ove krive?

Pretpostavimo da je kontrolna tačka P_k pomerena na novu poziciju P_k + v, gde vektor v određuje i pravac i dužinu pomeranja:

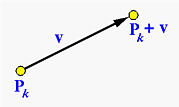
Početna Bézier-ova kriva je oblika:

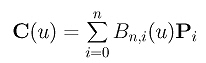
Kako je nova kriva određena tačkama P₀, P₁,..., P_k+v,..., P_n, njena jednačina D(u) je:

Kako samo k-ti sabirak koristi različitu kontrolnu tačku P_k + v, posle sređivanja izraza, dobijamo da se nova kriva predstavlja kao zbir početne krive i dodatnog člana B_n,k(u)v. Dakle:

Tačka u na novoj krivoj dobijena je translacijom odgovarajuće tačke u na početnoj krivoj u pravcu v na rastojanju |B_n,k(u)v|

Preciznije, za dato u, imamo tačku C(u) na početnoj, tačku D(u) na novoj krivoj i D(u) = C(u) + B_n,k(u)v. Kako v određuje pravac pomeranja, D(u) je rezultat pomeranja tačke C(u) u tom istom pravcu. Dužina pomeraja je, naravno, intenzitet vektora B_n,k(u)v, pa kada B_n,k(u) dostiže maksimum, promena iz C(u) u D(u) je najveća.

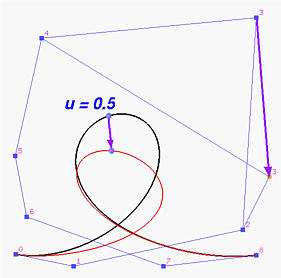
Na slici su date Bézier-ove krive 8. stepena definisane sa 9 kontrolnih tačaka. Početna kriva označena je crnom bojom. Ako pomerimo kontrolnu tačku 3 na novu poziciju, crna kriva se menja u crvenu. Na svakoj krivoj označena je tačka koja odgovara vrednosti parametra u=0.5. Pomeranje tačke C(0.5) u tačku D(0.5) vrši se u istom pravcu kao pomeranje kontrolne tačke na novu poziciju.

Kako je B_n,k(u) različito od nule na otvorenom intervalu (0,1), B_n,k(u)v nije nula vektor na (0,1). Ovo znači da se, osim krajnjih tačaka C(0) i C(1), sve tačke početne krive pomeraju na nove pozicije.

Promena pozicija kontrolnih tačaka menja oblik Bézier-ove krive globalno.