Podela Bézier-ove krive

Smisao podele krive je da "isečemo" datu Bézier-ovu krivu u tački C(u), za neko u, na dva dela, od kojih je svaki i dalje Bézier-ova kriva. Rezultujuće Bézier-ove krive moraju da imaju svoje kontrolne tačke, tako da se početni skup kontrolnih tačaka odbacuje. Štaviše, pošto se početna kriva stepena n deli na dve krive, od kojih je svaka podskup početne n-dimenzione Bézier-ove krive, i rezultujuće krive moraju biti n-tog stepena.

Problem je sledeći:

Za dati skup n + 1 kontrolnih tačaka P₀, P₁, P₂,..., P_n i parametar u vrednosti između 0 i 1, tražimo dva skupa sa n+1 kontrolnih tačaka Q₀, Q₁, Q₂,..., Q_n i R₀, R₁, R₂,..., R_n takvih da Bézier-ova kriva definisana pomoću Q_i (odnosno R_i) je deo početne Bézier-ove krive na [0,u] (odnosno [u,1]).

Algoritam je krajnje jednostavan i zasniva se na de Casteljau-ovom algoritmu za izračunavanje tačke C(u) na krivoj.
Na levoj slici predstavljen je de Casteljau-ov algoritam za izračunavanje C(u), a na desnoj podela krive u tački C(u) i njihove odgovarajuće poligonalne linije.

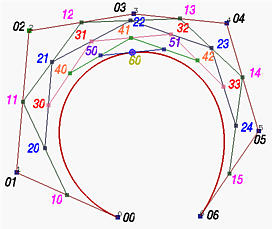
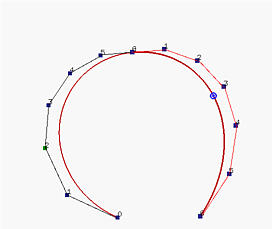
Ako pažljivo uporedimo ove dve slike, uočićemo da se leva poligonalna linija sastoji iz tačaka P₀₀ = P₀, P₁₀, P₂₀, P₃₀, P₄₀, P₅₀ i P₆₀ = C(u), dok je desna poligonalna linija određena tačkama P₆₀ = C(u), P₅₁, P₄₂, P₃₃, P₂₄, P₁₅ i P₀₆ = P₆. Na narednim slikama prikazan je način izbora ovih kontrolnih tačaka.

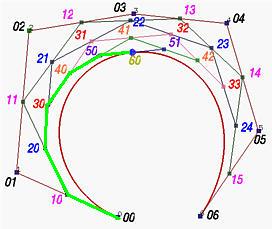
Za dato u, potrebno je n iteracija da se izračuna C(u). U procesu računanja, možemo pamtiti prvu i poslednju tačku u svakoj koloni i na kraju skup prvih (odnosno poslednjih) tačaka određuje deo početne krive definisan na [0,u] (odnosno [u,1]). Stoga, u sledećoj trougaonoj shemi gornja ivica u pravcu strelica i donja ivica u suprotnom pravcu određuju kontrolne tačke prve i druge podeone krive respektivno.

Primetimo da je duž određena tačkama 50 i 51 tangenta na krivu u tački 60, pa je poslednja duž poligonalne linije leve krive (npr. od tačke 50 do tačke 60) je tangenta na levu krivu, a duž poligonalne linije desne krive (npr. između tačaka 60 i 51) je tangenta na desnu krivu.

Zbog čega je potrebna podela Bézier-ove krive?

Podela krive ima veliki broj primena. Na primer, može se koristiti za određivanje preseka dve Bézier-ove krive, renderovanje Bézier-ove krive, a olakšava dizajn krivih. Pretpostavimo da smo formirali krivu koja nam ne odgovara sasvim. U tom slučaju, možemo je u odgovarajućoj tački podeliti na dva dela - zadovoljavajući i nezadovoljavajući. Tada se možemo fokusirati na promenu samo neodgovarajućeg dela.

Krivu možemo deliti proizvoljan broj puta, ali treba imati na umu da, ako želimo da se podeoni segmenti krive glatko spajaju, granične tačke i njihove dve susedne tačke moraju biti kolinearne.