
Primene računara (4. godina/ R smer) |
| A1 Navesti primer izračunavanja nk (k > 10) sa manjim brojem množenja nego u algoritmu Stepen_kvadriranjem (n, k) u glavi 8.2. |
REŠENJE:
Algoritam Stepen (n,k) (glava 8.2) nk=n*nk-1=> O(k)
| Algoritam Stepen_kvadriranjem (n,k) (glava 8.2) | nk=(nk/2)2 , k jeparan broj |
| nk=n*(n(k-1)/2)2 ,k je neparan broj | |
| T(k)=T(k/2) + 1 => a=1, b=2, O(k0 log k), tj. O(log k) | |
Broj množenja ne zavisi od n (zavisi od k).
Ako se više puta pojavljuje drugi slučaj nk=n*(n(k-1)/2)2,k je neparan broj, onda ukupan broj množenja je veći, a najgori slučaj je za k=2m-1 (tj. česta pojava drugog slučaja).
Pogledajmo primer najmanjeg k koje ispunjava uslov iz formulacije k > 10 i k=2m-1,tj. m=4, k=15:
Stepen_kvadriranjem (n, k) za k=15: n15= n* (n7)2=n* (n*n6)2= . . . = n* ( n* (n*n2)2) 2 => šest množenja
Ali, na primer n15=( ( (n2 ) 2 * n)3 => pet množenja
|
A2 Fibonačijevi brojevi su definisani sledećom diferencnom jednačinom: F( n ) = F( n-1 ) + F( n-2 ), ( n > 2 ) F(1) = F(2) = 1 Dokazati da se svaki prirodan broj n > 2 može predstaviti u obliku zbira najviše log2 n različitih Fibonačijevih brojeva. b) Konstruisati algoritam za određivanje takve predstave datog broja n. |
REŠENJE:
a) Dokaz principom matematičke indukcije:
baza: n=3 F(1)=F(2)=1, F(3)=2, F(4)=3 => n=F(4) && 1<log2 3
induktivna hipoteza: Za sve brojeve k manje od n važi
(IH) prirodan broj k > 2 može se predstaviti u obliku zbira najviše log2k-1 Fibonačijevih brojeva
Dokaz:
Dakle,postoji k: F(k)<=n<F(k+1) =>F(k) > n/2
/* supr. pretp. F(k)<=n/2. Kako je F(k-1) < F(k) za k>2, onda je F(k-1) < n/2
Odatle, F(k+1)=F(k)+F(k-1) < n/2 + n/2 =n što je kontradikcija sa n< F(k+1) */
Po (IH) za broj (n-F(k))potrebno je <= log2 (n-F(k)) razl. Fibonač. brojeva
Kako je n-F(k)< F(k), /* jer iz gore dokaznog svojstva F(k) > n/2 => 2*F(k)>n => F(k) > n-F(k)) */
onda F(k) ne učestvuje u reprezentaciji broja n-F(k) Fibonačijevim brojevima, te se za broj n= F(k) + (n-F(k))
koristi <= 1 + log2 (n-F(k)) razl. Fibonač. brojeva.
Kako 1+ log2 (n-F(k))=log22 + log2(n-F(k))=log2(2n - 2 F(k)) = log2(n + ( n- 2F(k))< log2n (jer n-2F(k) <0 po gore dokazanom)
b)
Algoritam Predstava (n)
input: n /* n>2 */
output: reprezentacija broja n kao sume Fibonačijevihbrojeva*/
{
f1=1; f2=1;
while (f2 <= n) {d=f1+f2; f1=f2; f2=d;} /* naci k: f(k)<=n < f(k+1) */
while (n>0) { if (n-f1>=0) { stampaj f1; n=n-f1;} d=f2-f1; f2=f1; f1=d;}
}
|
A3 Pokazati kako se kvadrat kvadratne matrice reda dva može izračunati pomoću pet množenja. |
REŠENJE:
Algoritam vrsta * kolona zahteva n3množenja,Vinogradov algoritam n3/2 + n2 množenja.
Za n=2 to je 8 množenja. Štrasen je otkrio da je potrebno sedam množenja elemenata da bi se izračunao proizvod ma koje dve matrice reda dva. (obavezno pogledati poglavlje 8.5.2)
Ako se radi o množenju dve iste matrice reda dva,tj. kvadriranju, onda je dovoljno izračunati pet proizvoda:
 |  | = | 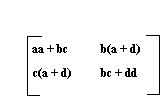 |
|
A4 Dato je n realnih matrica M1, M2, . . . , Mn. Matrica Mi je dimenzije ai× ai+1, 1 <= i <= n. Pretpostavimo da se proizvod matrica dimenzija ai × ai+1 i ai+1 × ai+2 izračunava algoritmom složenosti O ( ai ai+1ai+2) . U proizvodu M1M2 . . . Mntreba rasporediti zagrade (i time izabrati redosled množenja) tako da bude minimalan ukupan broj operacija. Konstruisati algoritam za nalaženje optimalnog redosleda izračunavanja proizvoda. |
REŠENJE:
Množenjem matrice M1 sa x vrsta, z kolona matricom M2 sa y vrsta, z kolona dobija se matrica R sa x vrsta, z kolona. Svaki od xz elemenata se dobija tako što se sabere nekih y proizvoda elemenata matrice M1 i M2,tako da je za množenje matrica potrebno ukupno xyz množenja.
U proizvodu M1M2 .. . Mn zagrade se mogu postaviti na više načina, a rezultujuća matrica ne zavisi od rasporeda zagrada (asocijativnost za proizvod matrica). Ali, ukupan broj množenja brojeva (elemenata matrica,ali i međurezultata) zavisi od rasporeda zagrada.
Neka je Opt[i, j] broj operacija u optimalnom množenju matrica MiMi+1 . . . Mj
Tada je:
| i=1..n 1<=i<j<=n | Opt [i,i] = 0 (bez množenja) |
| Opt [i,j] = mini<=k<j { Opt [i,k] + Opt [k+1, j]+ ai-1 ak aj } |
|
A5 Euklidov algoritam određuje najveći zajednički delilac za prirodne brojeve a0, a1. Na osnovu ideje Euklidovog algoritma, konstruisati algoritam koji pronalazi bar jedno celobrojno rešenje jednačine a0*x+ a1*y = NZD(a0,a1). |
Algoritam NZD (a0, a1)
input: a[0], a[1]
output: x, y
{
i=0; x[i]=1; y[i]=0;
i=1; x[i]=1; y[i]=0;
while ( a[i] % a[i-1] != 0)
{ q=a[i-1] / a[i];
a[i+1]= a[i-1]- q* a[i];
x[i+1]= x[i-1]- q* x[i];
y[i+1]= y[i-1]- q* y[i];
i++;
}
stampaj x[i], y[i]
}
Na primer: 57*x + 33*y = 3
| i | a[i] | x[i] | y[i] |
| 0 | 57 | 1 | 0 |
| 1 | 33 | 0 | 1 |
| 2 | 24 | 1 | -1 |
| 3 | 9 | -1 | 2 |
| 4 | 6 | 3 | -5 |
| 5 | 3 | -4 | 7 |
Dakle, x=-4, y=7
Da li je za svako i>=0 ispunjeno a[0]*x[i]=a[1]*y[i]=a[i] ?
DZ
i=0 => a[0]*x[0] + a[1]*y[0]=a[0]*1+0=a[0]
i=1 => a[0]*x[1] + a[1]*y[1]=0+a[1]*1=a[1]
IH: pretp. da važi za i-1, i, i>=2
Po algoritmu: x[i+1]= x[i-1] - q* x[i];
y[i+1]= y[i-1] - q* y[i];
Dakle, a[0]*x[i+1]=a[1]*y[i+1]= a[0] * (x[i-1] - q* x[i]) + a[1] * (y[i-1] - q* y[i]) = a[0]*x[i-1] +a[1]*y[i-1] -
- q * (a[0]*x[i] + a[1]*y[i]) = a[i-1] -q* a[i] = (po IH) a[i+1] => Q.E.D.
 | Naslovna - Jelena Grmuša |  | Primene računara |