Primene računara (4. godina/ R smer)

Redukcija ili svođenje nekih problema na već rešavane

Korisno je utvrditi može li se zadati problem rešiti ako se zna rešenje njemu sličnog problema. Mada ponekad put do utvrđivanja sličnosti dva problema vodi kroz složen proces redukcije zadatog problema na prethodno poznati problem. Naročito su interesantne redukcije među grafovskim algoritmima i grafovskim i matričnim algoritmima, kao i rešavanje problema linearnog i celobrojnog programiranja.

 

 

R1
Ako se zna da je 2n studenata konkurisalo na n fakulteta i ako je bipartitni graf   formiran od skupa čvorova studenata i skupa čvorova fakulteta tako da između studenta i fakulteta postoji grana ako i samo ako student ispunjava uslove za upis na taj fakultet, onda konstruisati algoritam za maksimiziranje broja primljenih studenata, uz uslov da niti jedan fakultet neće primiti više od dva studenta.

 

REŠENJE:

Problem liči na problem bipartitivnog uparivanja (zadatak 38), ali se ono ne može doslovce prepoznati, jer fakultet može biti u vezi sa viže studenata. Ali se može udvojiti svaki cvor koji odgovara fakultetima i povezati odgovarajuca dva cvora sa studentima koji su primljeni na taj fakultet.
Na taj nacin, problem je sveden na obican problem bipartitnog uparivanja.

 

R2
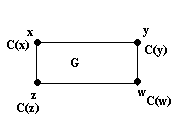
Dat je usmeren graf G=(V,E) sa izabranim čvorom v, takav da je svakom čvoru x pridružen pozitivan broj c(x). Cena usmerenog puta v, x1, x2, . . ., xk, u je definisana kao c(x1) + c(x2) + . . . +c(xk). Cene krajnjih tačaka puta, čvorova v, u se ignorišu(tj.ako grana (v,u) pripada grafu, cena puta od v do u je 0). Opisati algoritam za određivanje najjeftinijeg puta od v do svih ostalih čvorova.

 

REŠENJE:

graf G

Postoji asocijacija na algoritam za određivanje najkraćih puteva od v do ostalih čvorova u grafu. Ali,težine su pridružene čvorovima (ne granama).
Konstruisati novi graf F sa dva čvora w1 i w2 za svaki čvor w grafa G.

Skup grana odredjen je sa:

** za svaku granu (w,u) grafa G, grafu F dodati granu (w2,u 1) i pridruziti joj cenu 0.

** za svaki cvor u grafa G, dodati grafu F granu (u1,u2 ) i pridruziti joj cenu c(u).

Takvim nacinom formiranja grafa F se dati problem svodi na određivanje najkraćih puteva od čvora v2 do svih ostalih čvorova u grafu F.

graf G i graf F

 

R3

Dokazati da ako postoji algoritam složenosti O(T(n)) za množenje kvadratne n×n donje trougaone matrice kvadratnom n×n gornje trougaonom matricom, onda postoji algoritam složenosti O(T(n)+n2) za množenje dve proizvoljne n×n matrice. Pretpostaviti da T(cn)=O(T(n)) za proizvoljnu konstantu c > 0.

 

REŠENJE:

Neka su A i B dve proizvoljne kvadratne matrice reda n .
Svaka od njih se moze predstaviti kao zbir po jedne gornje i po donje trougaone matrice (TA, BA, TB, BB, redom):

A= T A + B A

B= T B + B B

Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B

Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati proizvod :

BA    0

T A BA 		 
×
  		TB BB
 
0    TB 		 
=
  		B AT B       BABB

T AT B       B AT B + T AB B

Kao rezultat dobija se matrica koja sadrzi blokove: B AB B , T AT B , B AT B + T AB B

Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.

Na taj nacin se problem izracunavanja proizvoda dve proizvoljne matrice svodi na problem izracunavanja proizvoda kvadratne donje trougaone matrice kvadratnom gornjom trougaonom matricom.

Ukupno vreme izvršavanja : O(T(2n)+n2 )=O(T(n)+n2)

 

R4 Ako je dat algoritam za mnozenje dve n * n donje trougaone matrice čije vreme izvrsavanja je O(T(n)), dokazati da postoji algoritam za mnozenje dve proizvoljne n *n matrice cije vreme izvrsavanja je O(T(n)+n2 

REŠENJE: Neka su A i B dve proizvoljne kvadratne matrice reda n .
Svaka od njih se moze predstaviti kao zbir po jedne gornje i po jednedonje trougaone matrice(TA, BA, TB, BB, redom):

A= T A + B A

B= T B + B B

Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B

Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati proizvod :

BA    0

T A BA 		 
×
  		BB    0
 
TB BB 		 
=
  		B AB B       0

T AB B+B AT B       B AB B

Kao rezultat dobija se matrica koja sadrzi blokove: B AB B , T AT B , B AT B + T AB B

Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.
Matrice ( TA )T i ( TB )T su donje trougaone matrice, te se upotrebom datog algoritma moze izracunati blok T A T B na sledeci nacin:

T A T B = ( ( TB )T ( TA )T )T
Ukupno vreme izvršavanja je O(T(2n)+n2)= O(T(n)+n2).
Na taj nacin se problem izracunavanja proizvoda proizvoljne dve matrice svodi na problem izracunavanja proizvoda dve kvadratne donje trougaone matrice.

 

R5 Dat je neusmereni povezani graf G=(V,E) sa n cvorova. Potrebno je ustanoviti da li u G postoji trougao (tj. takva tri cvora da između svaka dva od njih postoji grana). Konstruisati algoritam slozenosti O(nlog2 7) koji daje odgovor na ovo pitanje.

 

REŠENJE: Pogledati u knjizi prof. Živkovića poglavlje 10.2 i poglavlje 8.5.2

 

Jelena Grmuša Primene računara