Analiza algoritama

I

Algoritam koji zadovoljava rešenje formulisanog problema opisuje se

koracima
skupom ulaznih parametara
svojstvima koje moraju posedovati vrednosti na izlazu
skupom izlaznih vrednosti

Primer : Sortiranje

Input: a, N (a je niz od N celih brojeva ) a₁...a_n

Output: niz A sortiran u nerastućem poretku a₁ <= a₂ <= ... <= a_n

kôdiranje:

Zapis algoritama

shemom
pseudo-kôdom
programskim jezikom
prirodnim jezikom

kôdiranje programskim jezikom:

for(j=0; j<N-1; j++)
  for(k=j+1; k<N; k++)
if( A[j]>A[k] )
   {
     int rezerva;
     rezerva=A[j];
     A[j]=A[k];
     A[k]=rezerva;
    }

Ciljevi tokom ovog semestra: konstruisati algoritam koji je KOREKTAN i EFIKASAN.

Šta mislite, nad koliko test primera je potrebno propustiti program da bi proverili da je on korektan? Da li je dovoljno 2, 10, 1000 test primera?

II Korektnost

Potrebno je za svaki algoritam pokazati da uvek kao rezultat vraća očekivani izlaz za sve dozvoljene ulazne parametre formulisanog problema.

Na primer:
kod sortiranja izlaz mora biti neopadajući poredak niza A, čak i ako niz A
(1) već jeste sortiran, ili
(2) sadrži elemente koji se ponavljaju..

Primer 2

A) Konstruisati algoritam koji konvertuje dekadni broj u njegov binarni zapis.

Algoritam / pseudo-kôd za konverziju broja iz dekadne osnove u binarnu

Podsećanje na konverzije među osnovama

Algoritam DecToBin (n) ulaz: n /* n je prirodan broj */ izlaz: b /* b je niz cifara prirodnog broja n */ { /* početak bloka instrukcija */ lokalne promenljive bloka:

k /* indeks niza b */

t /* pomoćna promenljiva */

/*inicijalizacije*/

t=n; k=0;

while ( t > 0 ) { k=k+1 ; b[k]= t % 2 ; t= t / 2 ; /*celobrojno deljenje */ } } /* KRAJ */

B) Dokazati korektnost algoritma konverzija (tj. dokazati da se na kraju u nizu b nalaze binarne cifre broja n).

<=>

DOKAZATI: Ako binarni ekvivalent prirodnog broja m jeste niz b[1]...b[p], onda nakon svake iteracije ciklusa važi n=t*2^k+ m (invarijanta petlje), gde m, k, t, b su oznake promenljivih iz prikazanog algoritma

DOKAZ: principom matematičke indukcije, videti u knjizi Algoritmika

Princip matematičke indukcije -podsećanje *****

3. Dokazati da je za svaki prirodan broj n:

1 - 1/2 + 1/3 - ... + 1/(2n-1) - 1/(2n) = 1/(n+1) + 1/(n+2) + ... + 1/(2n)

Rešenje

Baza indukcije
za n=1: 1 - 1/2 = 1/2
Induktivna hipoteza (IH):
Pretpostavimo da je tvrđenje tačno za neki prirodan broj n i dokažimo da važi za n+1:

1 - 1/2 + 1/3 - ... + 1/(2n-1) - 1/(2n) + 1/ (2n+1) - 1/(2n+2)

= 1/(n+1) + 1/(n+2) + ... + 1/(2n) + 1/ (2n+1) - 1/(2n+2)

= 1/(n+2) + ... + 1/(2n) + 1/ (2n+1) + 1/(2n+2)

Šta znate o Fibonačijevim brojevima? Kakva je njihova uloga u računarstvu?

4. Dokazati da članovi Fibonačijevog niza (F₁=F₂=1, F_n=F_n-1 +F_n-2 za n >= 3) zadovoljavaju nejednakost

F_n <= φ^n-1

gde φ je broj (1+√5)/2

Rešenje

Za n=1:

F₁=1=φ⁰=φ^n-1, pa je baza indukcije dokazana (tj. da tvrdnja važi za n=1)

Za n=2:

F₂= 1<1.6<φ¹ =φ^2-1

Sada pretpostavimo (tj.postavimo IH) da je tvrđenje tačno za 1,2,...n i važi n>1.

To znači da tvrđenje važi i za n-1 tj. (i) F_n-1<=φ ^n-2

i važi za n, tj. (ii) F_n<=φ^n-1.

Dalje, za članove Fibonačijevog niza važi (iii) F_n+1=F_n-1 +F_n<=φ ^n-2 +φ ^n-1=φ ^n-2(1+φ ) .

Sada interveniše sledece svojstvo broja φ. Naime, neposredno se proveri da je φ²=φ +1

Stavljajući to u (iii) , dobija se: F_n+1<=φⁿ, pa je dokazano da je tvrđenje tačno za n+1. QED

Komentar primenjenje indukcije: Verovatno se secate da ako zelimo da dokazemo da je tvrdjenje P(n) tačno za sve prirodne brojeve n, onda postoje dva ključna poddokaza:
1) dokazati da je tacno P(1)
2) Ako je tacno P(1),P(2),...P(n) dokazati da je tacno P(n+1)
U našem zadatku obavljen je korak 1).
Ali pre koraka 2), pokazali smo direktnom proverom da je tvrđenje tačno za n=2. Da li je to bilo suvišno?
Odgovor: Ne, jer u koraku 2) od značaja nam je pretpostavka da tvrdjenje važi za n-1.
No, ako bi izostavili proveru za n=2 i pokušali da dokažemo da važi tvrđenje za n+1=2, onda bi morali da se oslanjamo na to da tvrđenje važi za F_n-1=F_1-1=F₀,
a ne možemo referisati na član F₀, jer taj član ne figuriše u formulaciji zadatka.

Za razmišljanje: Koji je odnos F_n i φ^n-2.

5.(strukture podataka) Dati su za n >=2 prirodni brojevi d_1, d₂,..., d_n takvi da im je zbir 2n-2. Da li postoji stablo sa n čvorova čiji su stepeni brojevi d₁, d₂,..., d_n ?

Rešenje

Odgovor je postoji. Dokažimo to.

Stepen čvora je broj grana koje su mu susedne. U mnogim zadacima se koristi cinjenica da sabiranje stepena cvorova d₁+...+d_n je isto sto i brojanje grana, pri cemu se svaka grana broji tacno dva puta.

Dakle, u ovom zadatku se radi nad stablom (ne mora da je binarno) i dokaz se izvodi indukcijom po n (broju čvorova)

Baza indukcije:
Ako n=2, onda d₁+d₂=2 =>d1=d₂=1 i postoji ovakvo stablo, jer dva čvora povezana granom jesu upravo stablo koje ima 2 čvora i to oba stepena 1
Induktivna hipoteza:
Pretpostavimo da je tvrđenje tačno za n-1 brojeva.
Induktivni korak: Neka je dato n>=3 prirodnih brojeva d_1,d₂,...,d_n čiji je zbir d₁+...+d_n=2n-2.
Tada postoje bar jedno i (1<=i<=n), bar jedno j(1<=j<=n) tako da d_i=1, d_j>1.
/* Obrazloženje: Pretpostavimo suprotno: Za svako i<=n da su d_i≠1. Tada su prirodni brojevi d_i>=2, tj. d₁+...+d_n >=2n, tj. ne može biti d₁+...+d_n=2n-2 (induktivni korak) QED
Slično za d_j se pretpostavi suprotno: za svako j <=n je d_j<=1 . Tada je d₁+..+d_n <=n, a znamo da za n>=3 je n<2n-2 Tada ne može biti d₁+...+d_n=2n-2 (induktivni korak) QED */

Izbacimo iz skupa d_i i umanjimo d_j za jedan i dobice se skup stepena cvorova za koji po induktivnoj hipotezi postoji stablo sa tim stepenima.
Zatim na to stablo dodamo novi cvor, zapravo list stepena d_i=1 prikacenog za cvor stepena d_j-1>=1 i dobija se stablo iz formuacije zadtaka, tj. stablo sa n čvorova stepena d_1,d₂,....d_n .
Jasno je da rešenje problema u opštem slučaju nije jedinstveno.

6.(Oprez sa indukcijom) Šta je pogrešno u sledećem "dokazu" kojim se želi dokazati tvrđenje:
Za svako pozitivno realno a i za svaki prirodan broj nje a^n-1 =1.
"Dokaz" : n=1 =>a^n-1 =a^1-1=1
Induktivna hipoteza: Pretpostavimo da je to tačno za 1,2,...,n
Tada: a^(n+1)-1=aⁿ= (a^n-1 * a^n-1) / a^n-2 = (1 * 1) / 1 =1, pa je takodje tvrđenje ispunjeno za n+1.
Rešenje
Problem je što nismo smeli pretpostaviti da je tvrđenje tačno za n=2.
Naime, u drugom delu dokaza, ako je 2=n+1 koristi se da imenilac a^n-2=1, ali ako je 2=n+1, onda n-2 =-1 i nije korektno pretpostaviti da a^-1=1.

Ovo bi bio kraj sažetog podsećanja na indukciju.

III Efikasnost

Da li je dovoljno da naš program radi korektno? Da li je potrebno da bude i efikasan?

Efikasnost se meri potrošnjom računarskih resursa pri izvršavanjem programa, a najznačajniji su vreme i prostor

Vreme izvršavanja

zavisi od sledećih faktora:

skupa mašinskih instrukcija računara na kom se algoritam izvršava, vremena njihovog trajanja u ciklusima, kao i trajanja jednog ciklusa
Na primer: i=i+1; i++; i+=1;
kvaliteta mašinskog kôda generisanog od strane prevodioca
Na primer: a=3; b=a+3; ILI a=3; b=6;
ulaznih podataka
vremenske složenosti algoritma

Faktori 1 i 2 zavise od konkretnog računara i prevodioca i ne odražavaju suštinu algoritma.

Vremenska složenost algoritama (svojstvo IV) se meri u odnosu na prebrojani broj upotrebljenih koraka.

IV RAM model

Analiza performansi algoritama u računarstvu se može odvijati i nezavisno od analize performansi hardvera ili konkretnog programskog jezika, iako kompletna analiza pretenduje da diskutuje i o uticaju tih parametara.

Za potrebe ALGORITMIKE se pri konstrukciji algoritama i diskusiji o njihovim osobinama koristi RAM model:

svaka "elementarna" operacija (+, -, =, if, višestruka selekcija) traje tačno 1 korak.
Petlje i pozivi potprograma nisu elementarne operacije i zavisne su od veličine podataka sa kojima rade i od sopstvenih podkoraka. Npr. sortiranje nije 1-koračna operacija.
Pristup memoriji se može uzeti za 1-koračnu operaciju.

Gore navedene pretpostavke važe sve dok se ne kaže drukčije.

V Najbolji, najgori i prosečan slučaj

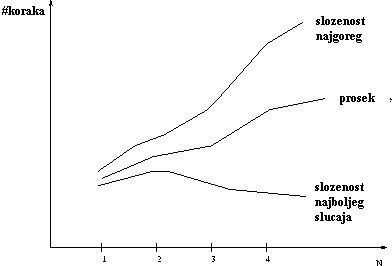
Složenost najgoreg slučaja algoritma jeste funkcija definisana u odnosu na najveći broj potrebnih koraka za obradu ulaza dimenzije n.

Složenost najboljeg slučaja algoritma jeste funkcija definisana u odnosu na najmanji broj potrebnih koraka za obradu ulaza dimenzije n.

Složenost prosečnog slučaja algoritma jeste funkcija definisana u odnosu na prosečni broj potrebnih koraka za obradu ulaza dimenzije n.

PRIMER 7: Sortiranje umetanjem

Niz od n elemenata se može sortirati tako što se pretpostavi da se n-1 elemenata mogu sortirati, a potom se umetne n-ti element na mesto koje mu pripada, tako što se pregleda n-1 sortiranih elemenata sve dok se ne pronađe odgovarajuđa pozicija za umetanje.

Dakle, počne se sa praznom listom , a potom se, umeću novi elementi na adekvatna mesta u nizu:

a₁<=a₂<=...<=a_k| a_k+1...a_n

U svakoj iteraciji, umetnuti element napušta sortiranu listu, i nakon do n umetanja pronalaze se korektne pozicije, te je otuda algoritam korektan.
Ali, koliko je on EFIKASAN?

Potrebno je uočiti koliko predsortiranost ulaza utiče na broj koraka, tj. slučaj već sortiranog niza u zahtevanom poretku i slučaj niza u obrnutom poretku i slučaj nesortiranog niza.

Precizna analiza algoritma

Prebrojmo koliko puta će se izvršiti svaka linija pseudokôda

Br linije InsertionSort(A) #Inst. #Izvrš.

1 for (j=1; j<n; j++) c1 1+(n-1)*1 +n-1

2 {pom=A[j]; c2 n-1

3 /* smesti A[j] unutar A[0..j-1] */ c3=0 /

4 i=j-1; c4 n-1

5 while (i>=0 &A[0]>pom) c5 t_j

6 {A[i+1]= A[i]; c6

7 i = i-1; } c7

8 A[i+1]=pom; } c8 n-1

for ciklus ima (n-1) iteracija

Unutar for ciklusa se dodela"pom:=A[j]" obavi n-1 puta.

Koraci 5, 6, 7:

Neka t_j je broj elemenat koji se moraju pomeriti udesno da bi se umetnuo j-ti element.

Korak 5 se izvrsava puta.

Korak 6: .

Ukupno vreme izvrsavanja algoritma je:

gde t_j su zavisni od ulaznih parametara (zbog relacije poređenja)

Najbolji slučaj

Ako niz jeste vec sortiran u zahtevanom poretku, onda su svi t_j jednaki 1.

Otuda je vreme najboljeg slučaja

gde C i D su konstante, tj. složenost je O(n)

Najgori slučaj

Ako je niz sortiran u obrnutom poretku, potrebno je pomeriti sve vec sortirane elemente, tako da

, a korak 5 se izvrsava za

Dakle, n-ti element se upoređuje sa svih prethodnih n-1 brojeva. U najgorem slučaju se u n-tom koraku premesta n-1 brojeva, te je i broj premestanja/kopiranja O(n²)

Dakle, ukupan broj uporedjivanje moze biti 1+2+...+n-1=n(n-1)/2=O(n²)

Ince, sortiranje umetanjem se moze poboljsati binarnom pretragom (ali ona ne utice na smanjenje broja kopiranja) ili ukrštanjem sa sortiranjem izborom.

Rekurentne relacije

8. Problem Pn sa parametrom n (n je prirodan broj) algoritam A rešava za T(n ) vremenskih jedinica.
Ako se zna da za svaki prirodan broj n vazi T(n+2)=3T(n+1)-2T(n), gde je T(1)=3, T(2)=5 odredi koliko vremenskih jedinica utrosi algoritam A za ulaznu vrednost n

Rešenje
Karakteristična j-na ove rek.j-ne je: t²-3t+2=0 <=> (t-1)(t-2)=0 =>t₁=1, t₂=2.
Tada je rešenje oblika T(n)=C₁*t₁ⁿ+C₂*t₂ⁿ
Iz početnih uslova: za n=1: 3=T(1)=C₁*1+C₂*2

Za n=2: 5=T(2)=C₁*1+C₂*2² =>C₁=1, C₂=1

Stoga, T(n)=2ⁿ +1

Problem Pn sa parametrom n (n je prirodan broj) algoritam A rešava za T(n) vremenskih jedinica. Ako se zna da za svaki prirodan broj n vazi T(n+2)=4T(n+1)-4T(n), gde je T(1)=6, T(2)=20 odredi koliko vremenskih jedinica utrosi algoritam A za ulaznu vrednost

Zbog dvostrukog korena se ovaj zadatak razlikuje od prethodnog.

Karakteristična j-na ove rek.j-ne je: t²-4t+4=0 <=>(t-2)²=0
Tada se rešenje traži u obliku T(n)=C1*t₁ⁿ+C₂*n*t₁ⁿ

Dakle za t₁=2 rešenje je oblika T(n)=C₁ 2ⁿ +C₂ n 2ⁿ

Iz početnih uslova: za n=1: 6=T(1)=C₁*2+C₂*2

Za n=2: 20=T(2)=C₁*4+C₂*8 =>C₁=1, C₂=2

Zato, T(n)=2ⁿ+ 2n *2ⁿ

10. Algoritam quicksort koristi strategiju "podeli pa vladaj" tj. izabere se element zvani pivot tako da pola elementa niza je manje ili jednako, a pola elemenata niza veće od pivota. Nakon razdvajanja niza rekurzivno se sortiraju dva podniza: levi i desni

Složenost algoritma je O(n log n). Zašto?
Označimo sa T(n) broj potrebnih vremenskih jedinica za rešavanje problema sortiranja quicksort-om niza dimenzije n.

Tada je
- T(2)=1
- T(n)= 2 T(n/2) + O(n) ( 2 rekurzije, plus const*N operacija za objedinavanje resenja)

Ova difrencna jednačina može da se reši tehnikom teleskopskih suma, ali i pozivom na Teoremu 2.1 iz knjige profesora Živkovića.

Teorema 2.1. Asimpototsko ponašanje niza T(n), rešenja difrencne jednačine

T(n) = a T(n/b) + c n ^k, a, b, c, k >=0, b !=0 i zadato je T(1)

dato je sa:

T(n)= O (n ^{log _b a}) za a > b ^k
T(n)= O (n ^klog n ) za a = b ^k
T(n)= O (n ^k) za a < b ^k

Kako je u algoritmu 3: a=2, b=2, a=b (tj. k=1), onda je T(n) = O (n log n)

11. Često prilikom analize vremenske složenosti mora se rešiti jednačina tipa full history T(n)=n+T(1)+T(2)+...+T(n-1), sa početnim uslovom T(1)=1

12. Sledeća rekurentna veza pojavljuje se u algoritmu tipa "zavadi pa vladaj" (algoritmi zasnovani na dekompoziciji ulaza na nejednake sastavne delove): T(n)=∑ _i=1..k a_i T(n/b_i) +cn, gde za konstante a_i , b_i važi ∑_i=1..k a_i/b_i <1
Pronaći asimptotsko ponašanje ove rekurentne veze.

Jelena Hadži-Purić Algoritmi i strukture podataka

e-mail: Jelena Hadži-Purić

Br linije	InsertionSort(A)	#Inst.	#Izvrš.
1	for (j=1; j<n; j++)	c1	1+(n-1)*1 +n-1
2	{pom=A[j];	c2	n-1
3	/* smesti A[j] unutar A[0..j-1] */	c3=0	/
4	i=j-1;	c4	n-1
5	while (i>=0 &A[0]>pom)	c5	t_j
6	{A[i+1]= A[i];	c6
7	i = i-1; }	c7
8	A[i+1]=pom; }	c8	n-1

Analiza algoritama

I

Ciljevi tokom ovog semestra: konstruisati algoritam koji je KOREKTAN i EFIKASAN.

Šta mislite, nad koliko test primera je potrebno propustiti program da bi proverili da je on korektan? Da li je dovoljno 2, 10, 1000 test primera?

II Korektnost

Primer 2

Algoritam / pseudo-kôd za konverziju broja iz dekadne osnove u binarnu

************** Princip matematičke indukcije -podsećanje *******************

III Efikasnost

Da li je dovoljno da naš program radi korektno? Da li je potrebno da bude i efikasan?

Efikasnost se meri potrošnjom računarskih resursa pri izvršavanjem programa, a najznačajniji su vreme i prostor

Vreme izvršavanja

Vremenska složenost algoritama (svojstvo IV) se meri u odnosu na prebrojani broj upotrebljenih koraka.

IV RAM model

V Najbolji, najgori i prosečan slučaj

PRIMER 7: Sortiranje umetanjem

Rekurentne relacije

Princip matematičke indukcije -podsećanje *****