Rekurzija i njene implikacije

Upotreba rekurzije: definicija matematickih funkcija, definiciju struktura podataka.

recur
latinski: re- = nazad +
currere = izvrsavati
Desiti se opet, u ponovljenim intervalima. Mnoge matematicke funkcije se mogu definisati rekurzivno:

3.4.2 Primer: faktorijel

Jedan od najjednostavnijih primera rekurzivnih definicija je faktorijel funkcija: 
faktorijel( n )
if ( n == 0 ) return 1;
                  else return (n * faktorijel( n-1 ))
Prirodan nacin za racunanje faktorijela je pisanje rekurzivne funkcije koja odgovara ovoj definiciji: 
int fact( int n )
        {
        if ( n == 0 ) return 1;
        else return n*fact(n-1);
        }
Ova funkcija poziva samu sebe da izracuna sledeci clan. Na kraju ce doci do uslova prekida i izaci. Medjutim, pre nego sto dodje do uslova prekida, ona ce staviti n poziva na stek poziva.

Postojanje uslov prekida je neophodno u radu sa rekurzivnim funkcijama. Ako se izostavi, tada ce funkcija nastavi da poziva samu sebe sve dok program ne popuni ceo stek poziva => neodgovarajuci rezultati!

Uporedite rekurziju i princip matematicke indukcije.

Da bi se izbegla beskonačna petlja u rekurzivnom pozivu, mora se uvesti trivijalni slučaj, odnosno slučaj koji predstavlja izlaz iz rekurzije. U primeru mnzoenja prvih n prirodnih brojeva, za slučaj n=0 proizvod prvih n prirodnih brojeva ne zahteva mnozenje, već odmah možemo vratiti rezultat. Ovde smo u funkciji faktorijel dodali slučaj za n=0 koji ne ulazi u rekurziju već samo vraća vrednost funkcije i to nam je trivijalni slučaj. Na ovaj način petlja poziva funkcije suma se zaustavlja u momentu kada n dobije vrednost 0. Jos jedan cesto koriscen (ali ne i efikasan) primer upotrebe rekurzivne funkcije je izracunavanje Fibonacijevih brojeva. Funkcija za generisanje n-tog člana Fibonačijevog niza: 

int fib( int n )
        {
        if ( (n == 0) || (n == 1) ) return 1;
        else return fib(n-1) + fib(n-2);
        }
Kratka i elegantna, ova funkcija koristi rekurziju da na lep nacin resi problem - ali je zbog neefikasnosti los izbor.

Analiza

Neka tn je broj koraka (vreme) potrebno da bi se izračunaofn, gde fn je nti Fibonaccijev broj.
Tada,
tn = tn-1 + tn-2
i
t1 = t2 = c,
gde c je konstanta.
Otud

tn = cfn
Dalje, asimptotski dobijamo resenje rekurentne veze

odnosno
te
tn = O(fn) = O(1.618..n)
=> funkcija zahteva eksponencijalno vreme, a takvi algoritmi se izbegavaju u programiranju!

Iterativno rešenje

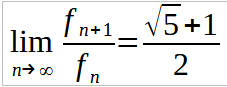
int fib( int n ) {
  int k, f1, f2;
  if ( n < 2 ) return n;
  else {
    f1 = f2 = 1;
    for(k=2;k<n;k++) {
      f = f1 + f2;
      f2 = f1;
      f1 = f;
      }
  return f;
}
Asimptotska složenost O(n) .

Algoritam iz f0 f1, najpre izračunava f2, te f3 iz f2 i f1, itd.

Stek poziva kod rekurzivnih funkcija
Po pravilu, programi kompajlirani u modernim jezicima visokog nivoa koriste stek poziva za radnu memoriju svake pozvane funkcije. Kada se pozove neka procedura ili funkcija, odredjeni broj parametara poziva se stavlja na stek poziva. Kada se vrsi povratak iz funkcije u pozivajuću rutinu, parametri poziva se skidaju sa steka.

Pored klasične rekurzije o kojoj je do sada bilo reči, postoji i takozvana uzajamna ili indirektna rekurzija koja se odnosi na situaciju kada dve funkcije jedna drugu pozivaju rekurzivno. Na ovaj način fukcija ne poziva samu sebe direktno, nego posredno preko druge funkcije.
Kada funkcija poziva drugu funkciju, najpre se njeni argumenti, zatim adresa povratka i konacno prostor za lokalne promenljive stavljaju na stek poziva. Posto svaka funkcija radi u sopstvenom "okruzenju" ili kontekstu, postaje moguce da funkcija pozove samu sebe - tehnika poznata kao rekurzija. Ova mogucnost je ekstremno korisna - jer se mnogi problemi elegantno specificiraju ili resavaju na rekurzivan nacin.

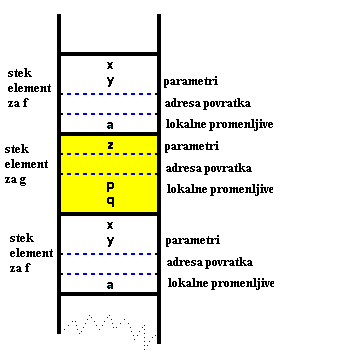stek poziva  Stek poziva posle izvrsavanja para uzajamno rekurzivnih funkcija:
int f(int x, int y) {
    int a;
    if ( uslov_prekida ) return ...;
    a = .....;
    return g(a);
    }

int g(int z) {
    int p,q;
    p = ...; q = ...;
    return f(p,q);
    }

Uociti da citava okruzenje funkcija f i g (njihovi parametri i lokalne promenljive) se nalaze na steku poziva. Kada se funkcija f pozove po drugi put iz funkcije g, kreira se novi format poziva za drugi poziv funkcije f.

Strukture podataka se takodje mogu rekurzivno definisati. Jedna od najvaznijih klasa struktura, poput stabla, dozvoljavaju rekurzivne definicije koje vode do rekurzivnih funkcija za njihovu obradu.

  Vaznost stabla uočimo na primeru pretraživanja. Uočimo i primer rekurzivne i nerukrzivne implementacije algoritam binarnog pretraživanja

Naslovna Osnovi programiranja