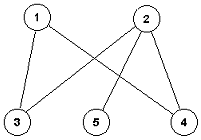
41. Dat je povezan neusmeren graf G=(V, E). Konstruisati algoritam koji će ustanoviti da li G jeste bipartitivni graf i u slučaju pozitivnog odgovora konstruisati razlaganje čvorova grafa u disjunktnu uniju. (Prema primeru 6.22 iz knjige, postoji tačno jedno ovakvo razlaganje za povezan bipartitivni graf G).
REŠENJE:
Neka čvor x pripada skupu od n čvorova V.
Baza indukcije: graf G sa 2 cvora
Induktivna hipoteza pretpostavlja da se problem ustanovljivanjada li G jeste bipartitivni graf i konstrukcija razlaganje čvorova grafa u disjunktnu uniju moze resiti za graf G'=(V', E'), podgraf grafa G sa n-1 cvorom.
1. Uklonimo čvor x i razložimo ostatak grafa G bez čvora x.(upotrebom indukcije) Neka smo dobili dva disjunktna podskupa. Označimo prvi od dva disjunktna podskupa sa A, a drugi skup sa B.
2.
2.1. Ako je x povezan samo sa čvorovima iz A, priključujemo čvor x skupu B i dobijamo skup B'. Jasno da skupovi A i B' su dva disjunktna skupa i jasno je da razlazu graf G (prema induktivnoj hipotezi).
2.2. Inače, ako je x povezan samo sa čvorovima iz B, priključujemo čvor x skupu A i dobijamo skup A'. Jasno da skupovi A' i B su dva disjunktna skupa i razlazu graf G (prema induktivnoj hipotezi).
2.3. Inače, ako je x povezan sa čvorovima iz A i B, onda graf nije bipartitivan, jer razlaganja je jednoznačno.
OVO REŠENJE NIJE KOREKTNO !!!
Naime, u koraku 2.3 koristi se da je graf nakon koraka 1 ostao povezan, što ne mora biti tačno => manji ulaz problema nije isti kao polazni ulaz problema, te se ni ne može koristiti indukcija.
Rešenje bi bilo korektno da je u koraku 1 izabran čvor x takav da graf G bez čvora x gradi graf G' koji je povezan.
IV2 Problem povezivanja kontira (oblast: računarska grafika): Spojiti učešljavanjem presek dve zadate konture.
Problem kontura se obrađuje u poglavlju 4.6 u knjizi.
PODSEĆANJE:
Jedan od primena u CAD, CAM, VLSI dizajn oblastima je i uklanjanje skrivenih linija unutar crteža ili pak izrada konture crteža.
Npr. zgrade jednog grada se zadaju kao uređen triplet ![]() gde
gde![]() i
i ![]() su leva i desna koordinata zgrade i,
su leva i desna koordinata zgrade i, ![]() je visina zgrade.
je visina zgrade.
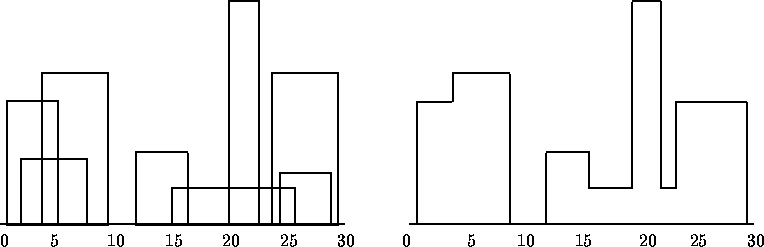
Na dijagramu levo niže zgrade su zadate redom tripletima
(1,11,5), (2,6,7), (3,13,9), (12,7,16), (14,3,25), (19,18,22), (23,13,29), (24,4,28)
dok na dijagramu desno niže kontura je zadata kao vektor
(1, 11, 3, 13, 9, 0, 12, 7, 16, 3, 19, 18, 22, 3, 23, 13, 29, 0)
gde uređeni parovi (1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18), (22, 3), (23, 13), (29, 0) opisuju levu koordinatu i visinu fragmenta konture. Ova kontura se moze naci formiranjem resnja ili induktivno ili dekompozicijom (razbijanjem na potprobleme, tj. pogledati poglavlje 4.6 u knjizi)
Dve konture su zadate pomoću dvaju nizova gde svaki zasebno čuva x, y koordinate, tj.:
Sky1x, Sky1y veličine n za I konturu Sky2x, Sky2y veličine m za II konturu
Rešenje su nizovi Sky3x, Sky3y, gde Sky3x je niz veličine n+m koji povezuju sortirane Sky1x, Sky2x, dok Sky3y sadrži niži od Sky1y, Sky2y ako se konture preklapaju, odnosno 0 ako se ne preklapaju.
REŠENJE:
Skica rešenja linerane složenosti
Neka su konture zadate pomoću dvaju nizova gde svaki zasebno čuva x, y koordinate, tj.:
Sky1x, Sky1y veličine n za I konturu Sky2x, Sky2y veličine m za II konturu
Rešenje su nizovi Sky3x, Sky3y, gde Sky3x je niz veličine n+m koji povezuju sortirane Sky1x, Sky2x, dok
Sky3y sadrži niži od Sky1y, Sky2y ako se konture preklapaju, odnosno 0 ako se ne preklapaju.
Inicijalizacija:
i = 0;j = 0;k = 0;
// napredovati ka prvoj presecnoj tacki tj. sve dok vazi ili
//Sky1x[i] < Sky2x[0] (prvi while ciklus) ili
//sve dok vazi Sky2x[j] < Sky1x[0] (drugi while ciklus)
// i postaviti na 0 visine (Sky3y[k]) svih tacaka koje prethode presecnoj
while (Sky1x[i] < Sky2x[0]) {
Sky3x[i] = Sky1x[i];
Sky3y[k] = 0;
i++; k++;
}
while (Sky2x[j] < Sky1x[0]) {
Sky3x[j] = Sky2x[j];
Sky3y[k] = 0;
j++; k++;
}
//glavna petlja
while (i<n) and (j<m)
{
// proveriti koja x vrednost se umece: da li iz I konture
if (Sky1x[i]<Sky2x[j])
{
Sky3x[k] = Sky1x[i]; // ubaciti x vrednost I konture
Sky3y[k] = min(Sky1y[i],Sky2y[j-1]); // ubaciti nizu visinu od dve moguce iz I i II konture
i++; k++;
}
else //ubaciti x vrednost II konture
{
Sky3x[k] = Sky2x[j];
Sky3y[k] = min(Sky1y[i-1],Sky2y[j]); // ubaciti nizu visinu od dve moguce iz I i II konture
j++; k++;
}
}
Jasno da algoritam je linerane složenosti, jer se elementarni koraci obavljaju jednim prolazom kroz niz.
V1. Dat je skup S od n realnih brojeva. Konstruisati algoritam složenosti O(n) koji pronalazi broj koji nije u S
Rešenje:
Taj broj može biti broj za jedan veći od najvećeg broja u skupu S.
Max svih brojeva se može naći jednim prolazom kroz skup S takošto se inicijalno postavi da je jednak 1. članu, a potom se prelazi kroz svaki sledeći član skupa i ukoliko je tekući član veći od max do tada, onda se promenljiva max ažurira i dobija vrednost tekućeg člana skupa S.
Kako se kroz skup S prolazi tačno jednom i za svakičlan obavljaju operacije poređenja sa promenljivom max i eventualna ažuriranja njene vrednosti (što je const vreme), onda je ukupna vremenska složenost O(n).
Algoritam manje slo ženosti ne može da rešava problem za svaki ulaz, jer ne može da pregleda svih n članova skupa S.
V2. Dat je skup S od n realnih brojeva i realan broj x. Konstruisati algoritam složenosti O(n log n) koji utvrđuje da li u S postoje dva elementa kojima je zbir jednak x.
Rešenje:
U opisanom algoritmu dominantan broj koraka potiče od koraka broj 1, čija donja granica složenosti je O(n log n)
za algoritme sortiranja zasnovane na upoređivanjima.
V3. Neka je E zadati niz brojeva x[1], x[2],..., x[n]. Višestrukost broja x u E je broj pojavljivanja x u E. Odrediti element E višestrukosti veće od n/2 ("preovlađujući element") ili ustanoviti da takav ne postoji.
na primer: 2 3 2 5 5 5 5 2 5 1 5 4 5 = > 5 je preovlađujući
Ideja 1 : izvrši se sortiranje, te ako postoji preovlađujući broj, on je u sredini i izvrši se za njega provera pozicije u sortiranom nizu. Može li efikasnije?
Ideja 2: Odrediti medijanu (videti u knjizi poglavlje o rangovskim statistikama - medijana je n/2-ti najmanji element), te je nađen kandidat za proveru. Može li efikasnije od O(n2)?
PODSECANJE: Formulacija problema rangovskih statistika: Za zadati niz elemenata S = x1; x2; ... xn i prirodni broj k, 1 <= k <= n, odrediti k-ti najmanji elemenat u S.
Kao i kod sortiranja razdvajanjem, los izbor pivota vodi
kvadratnom algoritmu.
Ideja 3: Ako je x[i] različito od x[j] i ako se izbace oba ova elementa iz niza, onda ako postoji y koji je preovlađujući element starog niza, onda je on preovladjujući element i novog niza (obratno ne važi).
U algoritmu se u jednom prolazu koriste promenljive C, M, gde C je jedini kandidat za preovladjujuci element u nizu x[0],x[1],..,x[i-1].
M je broj pojavljivanja elementa C u nizu x[0], x[1],...,x[i-1], bez onih elemenata C koji su izbaceni.
Ako je x[i]==C, onda se M uvecava za 1, a inace smanjuje za 1. (tada se smatra da x[i] moze biti izbacen zajedno sa nekim clanom jednakim C).
Ako M postane 0, onda C dobije novu vrednost x[i] i time i M postane 1.
Algoritam Preovladjuje (x,n):
ulaz: x, n /* niz pozitivnih brojeva x, dimenzije n*/
izlaz: preovlada /* preovladjujuci alaement (ako postoji) ili -1 */
C=x[0];
M=1;
for(i=1; i < n; i++)
if (M==0)
{C=x[i]; M=1;}
else
if (x[i]==C) M++; else M--;
if (M==0) preovlada=-1; /*nema preovladjujuceg elementa*/
else brojac=0;
for (i=0; i < n; i++)
if (x[i]==C) brojac++;
if (brojac > n/2) preovlada=C; else preovlada=-1;
V4.
Data su dva skupa realnih brojeva S1 i S2 i realni broj x. Ustanoviti da li postoje realni brojevi y1 iz S1 i y2 iz S2 takvi da im je zbir jednak x. Vremenska slozenost algoritma treba da bude O(n log n), gde je n ukupan broj elemenata u oba skupa.
REŠENJE:
Neka u prvom skupu ima k, a u drugom n-k elemenata.
1. Sortirajmo oba skupa u rastucem redosledu i oznacimo elemente prvog skupa posle sortiranja sa a1 a2 ... ak.
Oznacimo elemente drugog skupa posle sortiranja sa b1 b2 ....bn-k
2. Za svako i takvo da 1 <= i <= n - k: niz a1 + bi, a2 + bi, . . . , ak + bi je rastuci, pa se
binarnom pretragom pomocu O(log n) (preciznije [log k]+1) uporedjivanja medjuu ovim brojevima
pronalazi x, ili se utvrdjuje da ni jedan od njih nije jednak x.
Znaci, za proveru svih parova ai + bj dovoljno je O(n log n) uporedjivanja
SLOZENOST algoritma:
slozenost pocetnog sortiranja u koraku 1 je O(n log n)
za proveru svih parova ai + bj u koraku 2 dovoljno je O(n log n) uporedjivanja,
pa je ukupna slozenost algoritma O(n log n).
V5 Kutije su numerisane redom od 1 do n, gde je n paran broj.U i-toj kutiji je smeštena količina od a[i] objekata. Konstruisati algoritam koji će spojiti sadržaje po dve kutije, ali tako da maksimalna količina objekata u po dve kutije bude što je moguće manja.
Rešenje:
Dokaz korektnosti postupka:
=> dokaz da ma koje spajanje sadržaja po dve kutije različito od spajanja iz koraka 2, ima max količinu u po dve kutije ne manju od dobijene maksimalne količine u koraku 2
Pretpostavimo suprotno, tj. uočimo spajanje sadržaja po dve kutije koje umesto para (b[1], b[n]) ima parove(b[1], b[i]), (b[j], b[n])
Ako ta dva para se zamene parovima (b[1], b[n]), (b[i], b[j]), onda zbog (*), (**) se ne uvećava max zbirova, gde važi da:
(*) b[1]+b[n] <= b[j] + b[n]
(**) b[i]+b[j] <= b[j] + b[n]
Slično, ako se iz rezulatata koraka 2, umesto para (b[i], b[n-i+1]), i = 1 . . n/2
koriste drugi parovi,onda se opet n/2 puta primeni diskusija slična kao za (*), (**) uz zaključak da svih n/2 premeštanja parova imaju povećanje maksimuma zbirova => parovi (b[1],b[n]), (b[2], b[n-1]),..., (b[i], b[n-i+1]), i <= n/2, su optimalno rešenje zadatka.
V6.
Dat je niz od n prirodnih brojeva sa više ponavljanja elemenata, tako da je broj različitih elemenata u nizu O(log n).
a) Konstruisati algoritam za sortiranje ovakvih nizova, u kome se izvršava najviše O(n log log n) upoređivanja brojeva.
b) Zašto je složenost ovog algoritma manja od donje granice Ω(n log n) za sortiranje?
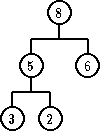
PODSEĆANJE: Stablo odlučivanja definiše se kao binarno stablo sa dve vrste čvorova, unutrasnjiim cvorovima i listovima. Svaki unutrasnji cvor odgovara pitanju sa dva moguca odgovora, koji su pak pridruzeni dvema granama koje izlaza
iz cvora. Svakom listu pridruzen je jedan od mogucih izlaza.
Gde se koristi ovo stablo? Stablo odlucivanja modelira izracunavanja koja se sastoje najvećim delom od upoređivanja. Koriste se kao model u dokazu da je slozenost svakog algoritma za sortiranje zasnovanog na poredjenju Ω(n log n)
Neka se sortira ulazni niz x1; x2;... xn. Izracunavanje pocinje od korena stabla. U svakom cvoru postavlja se jedno pitanje u
vezi sa ulazom, i u zavisnosti od dobijenog odgovora, nastavlja se levom ili desnom izlaznom granom. Kad se dostigne list, izlaz pridruzen listu je izlaz izracunavanja.
Na slici gore prikazano je sortiranje pomocu stabla odlucivanja za n = 3. Vremenska slozenost (u najgorem slucaju) algoritma definisanog stablom T jednaka je visini stabla T, odnosno najvecem mogucem broju pitanja koja
treba postaviti za neki ulaz. Stablo odlucivanja prema tome odgovara algoritmu.
REŠENJE:
a) Svaki element niza umetnuće se kao jedno polje čvora AVL stabla (ili nekog drugog tipa balansiranog binarnog stabla pretrage). Drugo polje čvora će čuvati broj pojava tog elementa u nizu. Ako je broj različitih elemenata u nizu O(log n), onda je broj čvorova u AVL stablu O(log n),
te je visina stabla O(log log n) => broj upoređivanja je najviše O(n log log n).
Zatim se stablo obilazi inorder obilaskom i njegovi elemeenti se kopiraju u neopadajućem redosledu u izlazni niz dužine n tako što se svaki element kopira onoliko puta kolika je vrednost odgovarajućeg brojačkog polja.
b) Opisani algoritam pod a) nije obuhvaćen modelom stabla odlučivanja, jer je pri konstrukciji algortma bilo od značaj da postoji relativno mali broj različitih elemenata u nizu, tj. vrednosti elemenata niza su bile značajne.
V7. Dat je hip sa n elemenata tako da najveći element je u korenu. Dat je i realan broj x. Konstruisati algoritam koji samo utvrđuje da li je k-ti najveći element hipa manji ili jednak od x. Nije nužno odrediti k-ti najveći element hipa. Vremenska složenost algoritma mora da (nezavisno od veličine hipa) bude O(k). Dozvoljeno je koristiti memorijski prostor veličine O(k) (u slučaju da se koristi rekurzija, dozvoljeno je koristiti memorijski prostor veličine O(k) za pamćenje rekurzivnih poziva, tj. za stek).
k-ti najveći element hipa veći od x <=> postoji k elemenata hipa koji su veći od x, k >= 0
broj=0; /* promenljiva koja cuva broj elemenata vecih od x; ova promenljiva mora ziveti, tj. cuvati vrednost izmedju rekurzivnih poziva,
te je staticka ili globalna ili ...*/
odgovor=NE; /* odgovor da li je k-ti najveći element hipa manji ili jednak od x */
Algoritiam Utvrdi (Hip H sa korenom v, x, k)
ulaz: H, k, x
izlaz: odgovor DA/NE
{
if (!v) return ODGOVOR;
if (v->vrednost > x) broj++;
if (broj > k) return (odgovor==DA);
Utvrdi(H sa korenom v->prviSin, x,k);
Utvrdi(H sa korenom v->drugiSin, x,k);
}
Bez obzira na veličinu hipa, broj rekurzivnih poziva f-je Utvrdi je O(k), jer algoritam se rekurzivno spušta niz hip H i uvećava promenljivu broj sve dok se ne prođe ceo hip H ili se ne izbroji k elemenata. Za pamćenje rekurzivnih poziva potrebno je koristiti stek, tj. memorijski prostor O(k)
Za razmišljanje: Za svako n koje je stepen dvojke navesti primer niza kod koga se pri sortiranju mergesort-om vrši maksimalan broj upoređivanja.
 | Jelena Grmuša |  | Primene računara |