Strukture podataka- primeri, primena i zadaci

• heap
• binarna stabla pretrage
• liste povezanosti
• hash tabele
• Zadaci

Zadaci

Teorijska osnova: Hip - primeri i primena

I 1. Neka A je vektor koji se koristi za implicitno predstavljanje hipa. Koliki najmanji broj elemenata može da zauzme niz dužine 16?

REŠENJE: Kako je zauzeto polje na poziciji 16 => mora biti zauzeto i polje na poziciji 8 za čuvanje oca čvora 16. Zato što po definiciji implicitne reprezentacije stabla preko niza, element A[16] odgovara čvoru čiji predak je čvor pridružen elementu A[8]. Sličnim rezonom, dolazi se do zaključka da moraju biti zauzete za pretke i pozicije 4, 2, 1. Dakle, minimalan broj elemenata je 5. ( log₂16 +1)

I 2. Konstruisati algoritam insert() koji ubacuje element x u prioritetni red Q i konstruisati algoritam delete_min() koji uklanja najmanji element prioritetnog reda. Kolika je vremenska slozenost algoritama ako se prioritetni red realizuje kao linearna sortirana lista, a kolika ako se realizuje kao kompletno binarno stablo koje je predstavljeno dinamickim nizom svojih elemenata. Smatrati da red je uređen relacijom '<', tj. svako dete mora biti veće od svog roditelja

REŠENJE:

Prioritetni red se može relativno jednostavno realizovati pomoću linearne sortirane liste. U tom slučaju operacija delete_min() ima vremensku složenost O(1), jer se zapravo pronalazi i izbacuje prvi element u listi,

Operacija insert() mora ubaciti novi element na "sortirano mesto". To znači da u proseku treba obići bar pola sortirane liste, pa vremenska složenost operacije insert() jeste O(n).

Efikasnija implementacija se može napraviti pomoću hipa (eng. heap), gde hip je kompletno binarno stablo koje je zapisano pomoću niza elemenata, prema pravilu 1 i 2:
1. ako element indeksa i predstavlja čvor stabla, tada
- element indeksa 2*i+1 predstavlja levo dete čvora,
- element indeksa 2*i+2 predstavlja desno dete čvora,
- element indeksa (i-1)/2 predstavlja roditelja čvora

2. ključ roditelja nekog čvora uvek je manji od ključa tog čvora, pa je najmanji ključ u korenu stabla

POSLEDICA PRIMENE PRAVILA 1 i 2:
- indeks namanjeg elementa (koji je u korenu stabla) jednak je i = 0.
- indeks kranjeg elementa je N-1. To je krajnji desni list stabla.
Kapacitet niza treba biti veći od broja elemenata niza. Zbog toga je povoljno da se niz realizuje kao dinamički niz koji se može povećavati (realocirati) ako, pri operaciji umetanja, broj elemenata niza dosegne kapacitet niza.

Neka je clan prioritetnog reda, tj. heap-a definisan sa

typedef struct pq_elem { /* element prioritetnog reda */
  int key; /* ključ za postavljanje prioriteta */
  void *val; /* vrednost elementa (bilo šta) */
} elemT;

Neka je prioritetni red opisan sa

typedef struct pq {
  int kapacitet; /* kapacitet prioritetnog reda*/
  int N; /* broj umetnutih elemenata */
elemT *elementi; /* niz elemenata reda */
} PQueue, *PQUEUE;

Umetanje elementa u prioritetni red


Ako želimo dodati element u prioritetni red možemo ga dodati na kraj niza. To je ekvivalentno dodavanju krajnjeg desnog lista u stablu. Ta operacija ima za
posledicu da se N uveća za jedan, ali i da možda stablo ne zadovoljava pravilo hipa. Da bi se zadovoljilo pravilo hipa koristi se postupak opisan u sledećem algoritmu:
Algoritam: Umetanje
1. Element iza krajnjeg elementa niza se tretira kao prazan (to je sledeći krajnji desni list stabla). Podrazumeva se da je kapacitet niza veći od broja elemenata u nizu.
2. Ako je ključ roditelja praznog čvora manji od ključa elementa x, tada se element x
upisuje u prazni čvor. Time je postupak završen.
3. Ako je ključ roditelja praznog čvora veći od ključa elementa x, tada se element roditelja
kopira u prazni čvor, a čvor u kojem je bio roditelj se uzima kao prazni čvor. Postupak
se ponavlja korakom 2.


Prethodni algoritam je primenjen u funkciji insert(). U toj funkciji se najpre
proverava da li je popunjen kapacitet reda. Ako je popunjen, dvostruko se povećava kapacitet
reda. Nakon toga se vrši umetanje elementa prema prethodnom algoritmu.

/* Funkcija insert() umeće element u red
* Argumenti: pQ - red
* x - element koji se umeće
*/
void insert(PQUEUE pQ, elemT x)
{
int i;
assert(pQ);
/* proveri kapacitet reda i povećaj ga ako je N>=kapacitet*/
if ( pQ->N >= pQ->kapacitet-1 ) {
pQ->kapacitet *= 2; /*udvostruci kapacitet hipa*/
pQ->elementi = (elemT *) realloc(pQ->elementi,sizeof(elemT)*pQ->kapacitet);
if(!pQ->elementi) exit(1);
}

/* umetni element x i povećaj N */
i = pQ->N++;
while (i) {
int otac = (i-1)/2;
if (x.key > pQ->elementi[otac].key) break; /*pravilo 2 algoritma */
pQ->elementi[i].key = pQ->elementi[otac].key;
i = otac;
}
pQ->elementi[i] = x;
}


Brisanje minimalnog elementa iz prioritetnog reda

Brisanje elementa iz prioritetnog reda se vrši samo na jedan način: briše se element s
minimalnim ključem pomoću funkcije delete_min(). Minimalni element se nalazi u korenu
stabla, odnosno u hipu na indeksu 0. Ako ga izbrišemo tada je koren prazan i u njega treba
zapisati neki drugi element. Najzgodnije je u njega zapisati krajnji element niza (vrh) i smanjiti
veličinu hipa. Problem je što tada možda nije zadovoljeno pravilo hipa. Dovođenje niza u
stanje koje zadovoljava pravilo hipa vrši se funkcijom uredi(), prema sledećem algoritmu:


Algoritam: uređenje hipa kada vrh hipa nije u skladu s pravilom hipa
1. Započni s indeksom koji predstavlja vrh hipa i smesti taj element u promenljivu x. Nadalje
se uzima da je vrh hipa "prazan".
2. Analiziraj decu praznog čvora i odredi koje dete je manje.
3. Ako je ključ od x manji od ključa manjeg deteta smesti x u prazan čvor i završi,
inače upiši element manjeg deteta u prazan čvor i postavi da čvor manjeg deteta bude
prazan čvor. Ponovi korak 2.

void uredi(elemT *elementi,int vrh, int N)
{
int min_dete, i = vrh;
/*zapamti element kom se traži mesto u hipu */
elemT x = elementi[i];


/* (i) označava "prazni" element*/
while (i < N/2) {
int left = min_dete = 2*i+1;
int right = left + 1;


/* Prvo odredi indeks manjeg deteta - min_dete */
if ( (left < N-1) && (elementi[left].key > elementi[right].key) )
min_dete = right;


/* Ako je min_dete manji od x, upiši ga na prazno mesto (i), inače break */
if ( x.key < elementi[min_dete].key) break;
elementi[i] = elementi[min_dete];
i = min_dete;
}
/* konačno stavi x na prazno mesto*/
elementi[i] = x;
}


Sada je implementacija funkcije delete_min() jednostavna. U njoj je najpre zapamćen minimalni element, koji je na indeksu 0, u promenljivoj minimum. Zatim je krajnji element upisan na početak niza, a veličina hipa je smanjena. Sledi poziv funkcije uredi(), kojom se uređuje hip, ako je poremećeno pravilo hipa.

/* Briše najmanji element iz reda PQ
* Vraća: element koji je izbrisan*/

elemT delete_min(PQUEUE pQ)
{
elemT minimum;
assert(pQ);
assert( pQ->N > 0 );


/* minimum je u korenu (indeks 0) */
minimum = pQ->elementi[0];


/* zadnji element prebaci u koren i smanji veličinu hipa*/
pQ->elementi[0] = pQ->elementi[--pQ->N];


/* preurediti hip od vrha prema dnu (vrh je na indeksu 0) */
uredi(pQ->elementi, 0, pQ->N);
return minimum;
}

PRIMER UMETANJA I BRISANJA

Ako se u hip ubace brojevi:
42 68 35 1 70 25 79 59 63 65
onda izlaz iz prioritetnog reda algoritmom delete_min() glasi:
1 25 35 42 59 63 65 68 70 79
Vidimo da je izlaz sortiran, jer smo iz reda brisali jedan po jedan minimalni element.

Vremenska složenost operacija insert() i delete_min(): obe operacije se obavljaju samo po jednoj stazi od vrha do dna hipa ili obrnuto. Kod potpunog stabla duzina te staze iznosi
log(n+1)-1. Pošto nas zanima asimptotska vrednost (za veliko n), vremenska složenost iznosi O(log n).

I 3. Konstruisati algoritam koji formira hip sačinjen od elemenata dva hipa čije veličine redom su m i n. Hipovi su predstavljeni eksplicitno (tj. stablom, tj. svaki čvor ima pokazivače na svoja dva sina i uređeni relacijom '>', tj. svako dete mora u heap-u biti manje od oca). Vremenska složenost algoritma u najgorem slučaju mora biti O( log(m+n) ).

REŠENJE:

1. uklanja se proizvoljan element iz nekog hipa (npr. veći koren) i izvedu se popravke hipa na način koji je opisan u sekciji uklanjanja elementa iz hipa

2. izabrani element se umeće kao koren novog hipa, tako da njegovi sinovi budu koreni dva stara hipa

Popravka dobijenog hipa (stabla) uz eventualno premeštanje naniže elementa iz korena zahteva O( log(m+n)) koraka zbog dimenzije novog hipa.

Teorijska osnova: binarna stabla pretrage

II 1. Kolika je složenost poznatog rekurzivnog algoritma koji BSP štampa u inorder obilasku čvorova, tj. formira neopadajući niz od ključeva elemenata iz BSP?

REŠENJE: Broj rekurzivnih poziva jednak je broju čvorova stabla n, a trajanje svakog pozova je O(1), te je složenost algoritma O(n).

Željeni niz dobija se nadovezivanjem niza koji odgovara levom podstablu, ključa korena stabla i niza koji odgovara desnom podstablu.

III1. Odrediti najmanji i najveći broj čvorova koje može da ima AVL stablo visine h .

REŠENJE:

PRVI DEO ZADATKA je određivanje najvećeg broja čvorova za AVL stablo visine h.
Neka je G_h oznaka za najveći broj čvorova stabla visine h.

Važi

G₀=1 (samo koren čini AVL stablo visine 0),
G₁=3 (koren i levo i desno dete čine AVL stablo visine 1),
G₂=7 (koren, levo i desno dete, levi i desni unuk kao deca levog deteta, levi i desni unuk kao deca desnog deteta čine stablo visine 2) i:

N_h=N_h-1+N_h-2+1
N_h+1=N_h+N_h-1+1
N_h+1- N_h = N_h +N_h-1+1- N_h-1- N_h-2-1
N_h+1 - 2N_h + N_h-2=0
Karakteristična jednačina ove rekurentne veze je
t³-2t²+1=0
odnosno (t-1)(t²-t-1)=0
odnosno njeni koreni su t₁=1, t₂= (1 +5^1/2)/2, t₃= (1 - 5^1/2)/2
Zato je opsti član niza N_h jednak
N_h = C₁ + C₂ * ((1 + 5^1/2)/2)^h + C₃ * ((1 - 5^1/2)/2)^h

Rešenja sistema su:
C₁ = - 1
C₂ = (5^1/2+2) /5^1/2
C₃ = (5^1/2- 2) /5^1/2

III2. Elementi (međusobno različiti) nekog skupa S su smešteni u binarno stablo pretrage visine h. Konstruisati algoritam složenosti O(h) koji za dati element a skupa S određuje sledeći po veličini element skupa S.

Pretpostavimo da je stablo građeno tako da je informaciono polje (ključ) desnog sina veće ili jednako od informacionog polja (ključa) oca.

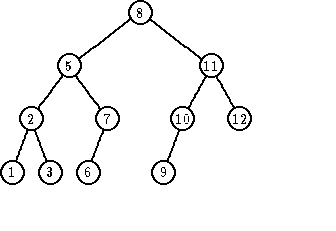
Sledbenik zadatog čvora je čvor sa najmanjim ključem koji je veći od ključa datog čvora.

Koji čvor nema sledbenika? Samo najdešnji čvor u stablu (koji nema desnog sina i koji je desni sin svog oca), jer je on čvor sa maksimalnom vrednošću ključa. (Na primer a=12)

Karakteristični slučajevi za čvor v čije informaciono polje (ključ) ima vrednost elementa a iz skupa S su:

1. v ima desno podstablo
=> Sledbenik se traži kao ključ desnog sina, odnosno kao ključ najlevljeg čvora u desnom podstablu

Na primer: a=8 ili a=5 ili a=11

2. v nema desnog sina
=> Sledbenik se traži tako što se traži ključ najnižeg pretka w takvog da levi sin od w je predak čvora v.

Ova operacija se najefikasnije izvodi ako se za svaki čvor čuva i polje otac sa pokazivačem na oca čvora. Tako se ide od čvora v prema korenu sve dok se ne nađe čvor w koji je levi sin svog oca. U slučaju da nema takvog pretka w, onda je a najveći element skupa i nema svog sledbenika.

Na primer: a=12 ili a=3

Sledi algoritam za nalaženje sledbenika za zadatu vrednost ključa čvora ukazanog sa v koji vraća adresu sledbenika ili NULL. Koristi se i poziv algoritma BST_MIN koji u BST (stablu binarnog pretraživanja) traži ključ sa minimalnom vrednošću.

Algoritam BST_MIN za BST čiji je koren ukazan argumentom node ide po lancu levih pokazivača sve dok ne dođe do čvora koji nema levog sina. Radili smo ga na proslom casu.

Algoritam BST_MIN pokriva 1. situaciju kada je potrebno pronači ključ sa minimalnom vrednošću u desnom podstablu čvora v.

Algoritam BST_SLEDBENIK (v)

ulaz: v

izlaz: q /* bilo da je NULL ili nije */

{

     pom=v

     if (right(pom) != NULL)  return BST_MIN(right(pom))  /*1. situacija*/

     else                 /* 2. situacija*/

        {

             q=otac(pom)

             while (q != NULL ) and  (pom == right(q))  do

              {

                   pom=q

                   q=otac(pom)

              }

            return q

        }

}

Napomena:  x=right(y)  <= > x=y- > right  . . .

Operacije nalaženja minimalnog ključa, sledbenika imaju vreme izvršavanja srazmerno visini stabla h, tj. O(h), jer u svakoj od situacija prate putanju kroz stablo samo u jednom smeru.

Umetni (x)	umetanje ključa x u strukturu podataka (ako već ne postoji)
Obrisi (x)	brisanje ključa x iz strukture podataka (ako postoji u strukturi)
Naredni (x)	pronalaženje najamanjeg ključa u strukturi podataka koji je veći od x

Izvršavanje svake od ovih operacija treba da ima vremensku složenost O(log n) u najgorem slučaju, gde je n broj elemenata u strukturi podataka.

Rešenje:

Za realizaciju navedenih operacija, pogodna struktura podataka je AVL stablo u kome se umetanje i brisanje izvršava za O(log n) koraka.

Za izvođenje operacije Naredni (x) koristi se

• najpre algoritam pronalaska ključa x (O(log n))
• potom se kao u prethodnom zadatku  pronalazi sledbenik u stablu (O(log n)).

III4. Konstruisati algoritam čija vremenska složenost je linearna po broju čvorova binarnog stabla i koji u stablu markira (označava) sve S-AVL čvorove čiji niti jedan potomak nije S-AVL čvor. Smatrati da čvor binarnog stabla je S-AVL čvor ako nije list i ako razlika visina njegovog levog i desnog podstabla je jednaka 0.

Algoritam SAVL (stablo x)

 ulaz: stablo x

 izlaz: dubina stabla kao oznacen broj

/* CILJ: ako algoritam vrati dubinu <0, to znači da se u stablu kao potomak pojavljuje SAVL cvor

               ako algoritam vrati dubinu 0, to znači da stablo je list

              algoritam vrati dubinu >0, to znači da SAVL čvor jos nije nađen

  IDEJA:

1.  Ako su dubine levog i desnog podstabla jednake i ako ni u levom ni u desnom podstablu se ne nalazi SAVL čvor (jer je vracena dubina >0),

tada se taj čvor markira, jer je SAVL čvor (npr. sa x->oznaka=1;). U tom slucaju vraća se negativna dubina stabla.

2.  Ako nisu dubine levog i desnog podstabla jednake ili ako se  u levom ili u desnom podstablu nalazi neki SAVL čvor (jer je vracena dubina <0),

tada se vraća dubina drveta sa predznakom, zavisno od toga da li je nađen SAVL čvor ili ne.

{

     if (x==NULL)  return 0; 
    else
       { 

            levo=SAVL(x->levo);
            desno=SAVL(x->desno);
         if (levo >0 && desno >0)
              if (levo==desno)  /*situacija 1*/
                   { x->oznaka=1; return -(levo+1);}
             else return max(levo, desno) +1;
        else return  -( 1+ max (abs(levo), max(abs(desno));
}

Složenost algoritma

  za n=1,  T(n) =c1 (const za obradu stabla sa jednim cvorom)

   za n>1, T(n)=n*c1*c2  (c2 je cena vremena koje obuhvata rekurzivni poziv SAVL algoritma i povratka) =>  T(n)=O(n)  q.e.d.

III5. Konkatenacije je operacija nad dva skupa koja zadovoljavaju uslov da su svi ključevi u jednom skupu manji od svih ključeva u drugom skupu. Rezultat konkatenacije je unija skupova. Konstruisati algoritam za konkatenaciju dva binarna stabla pretrage u jedno stablo. Vremenska složenost algoritma mora biti O(h) u najgorem slučaju, gde h je veća od visina dva stabla.

REŠENJE:

 Neka su zadata dva BSP stabla T, G, tako da svi ključevi stabla G su veći od svih ključeva stabla T.

Neka je bez smanjenja opštosti visina h stabla G veća od visine stabla T.

1. Pronaći u stablu G čvor v sa najmanjim ključem (npr, sve dok je moguće spuštati se niz stablo polazeći od korena ulevo i to se može obaviti za O(h) vremena)

2.  Ukloniti čvor v iz stabla G  (O(h) vremena)

3.  Formirati za O(h) vremena novo stablo sa korenom v čija podstabla su stabla T (levo) i stablo G bez čvora v (desno) ). Novoformirano stablo ostaje binarno stablo pretrage, jer koren, tj.  čvor v je sa najmanjim ključem u G, tako da desno podstablo može biti G. S druge strane, po uslovu s početka, svi ključevi stabla G (pa i v) su veći od svih ključeva stabla T, te T može biti levo podstablo.

III6. Isto to, ali za AVL stabla, tj. neka stabla T i G iz rešenja nisu samo BSP stabla, već AVL stabla.

REŠENJE:

Neka su zadata dva AVL stabla T, G, tako da svi ključevi stabla G su veći od svih ključeva stabla T.

Uz čvorove stabla T i G čuvaće se i informacija o visini, jer je to svojstvo značajano za AVL stabla, kao tip balansiranih stabala i neka je,

na primer, visina h₂ stabla G sada manja ili jednaka od visine h₁ stabla T. Drugi slučaj rešava se analogno.

1. Ukloniti najveći čvor iz stabla T, na primer čvor r  i on će kao u prethodnom zadatku biti koren stabla preko kog se stablo G privezuje za T. Evo kako.

2. Spuštajući se u stablu T desnim granama, naći čvor v visine h₂ ili h₂-1 (a to je moguće jer h₁>=h₂). Neka otac čvora v jeste čvor p.

3. Postaviti da desni sin čvora p ne bude cvor v, vec čvor r iz koraka 1. (što je održava poredak, jer čvor r je sa najvećim ključem, te može biti desni sin čvora p)

4. Postaviti da levi sin čvora r bude cvor v sa podstablom T, a desni sin koren G. To je u redu sa stanovista BSP svojstva, jer r je najveci čvor u T. te je ključ čvora v ne veći od njega i može biti levi sin, a kako svaki čvor stabla G, te i koren je veći od najvećeg ključa iz T, onda koren iz G može biti desni sin sa ciljem da i novoformirano stablo bude binarno stablo pretrage (BSP).

5. U koracima 3 i 4 formirano je stablo koje ima BSP svojstva, ali možda nije uravnoteženo, tj. visina čvora r može da postane veća za 1 od visine čvora v koji je bio na tom mestu, te je nuzno obaviti eventualno uravnotezenje pomocu rotacije.

Sve operacije traju <=O(h₁) koraka zbog svojstva AVL stabla.

III7.

AVL stablo visine h ima bar F_h+3 - 1 čvorova, gde F_i   je i -ti Fibonačijev broj (h>=0).

Dokaz:

Neka T_h je ukupan broj čvorova (dakle, ne ukupan broj unutrašnjih čvorova) u AVL stablu D_h visine h sa najmanjim mogućim brojem čvorova.

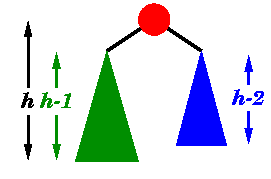
Jasno da je

T₀=1

T₁=2

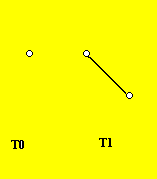
Takođe

T₀ = F₃ -1 = 2- 1 =1

T₁ = F₄ -1 = 3- 1 =2

Kako D_h je AVL stablo visine h sa najmanjim mogućim brojem čvorova, to ono mora imati podstabla visine h-1 i h-2 (zato što bar jedno podstablo mora biti visine h-1, dok zbog uslova balansiranosti  visina podstabala se mora razlikovati najviše za jedan). Takodje, ta podstabla moraju biti stabla visine h-1, odnosno h-2, sa najmanjim mogućim brojem čvorova.

Otuda važi relacija:

T_h=T_h-1+T_h-2+1

< = > T_h+1 = (T_h-1+1) + (T_h-2+1)

Za vrednosti T_h+1 važi ista diferencna j-na kao i za Fibonačijeve brojeve F_h:

F₁ = F₂

F_{h + 2} = F_{h + 1} + F_h , h >= 2

Dokaz se, dalje, kompletira korišćenjem indukcije.

Teorijska osnova: Liste povezanosti

IV1.

Za graf koji ima n čvorova i m grana odrediti potreban prostor za predstavljanje grafa matricom povezanosti ili listom povezanosti.

IV2.

Za graf koji ima n čvorova i m grana odrediti da li je predstavljanje grafa pogodnije matricom povezanosti ili listom povezanosti u sledecim situacijama:

1. provera da li grana (x, y) pripada grafu        

2. redak graf (m<<n*n)

3. dodavanje ili brisanje grana iz grafa

4. markiranje grana

5. obilazak grafa

IV3.  

Neka je G=(V,E) stablo sa n čvorova. Cilj je formirati simetričnu kvadratnu matricu reda n, čiji elemenat (i,j) je jednak rastojanju između čvorova v_i i v_j. Konstruisati algoritam složenosti O (n ²) koji rešava ovaj problem ako je stablo zadato listom povezanosti.

• rešenje je jednostavno za stablo sa jednim ili dva čvora
• neka je pretpostavka da se zna rešiti problem za stablo sa n-1 čvorova

  POLAZNE PRETPOSTAVKE I OZNAKE:

  Neka je dato stablo S sa n čvorova i

  neka v je list tog stabla i

   neka w je jedini čvor susedan sa v (po definiciji lista u binarnom stablu, jasna je njegova egzistencija i jedinstvenost).

  POSTUPAK

  Uklanjanjem lista v iz S dobija se stablo S^' sa n-1 čvorova, za koje se u O (n ²) koraka može izračunati matrica svih rastojanja (sledi iz induktivne hipoteze).
  

  1. Neka su u, t proizvoljan čvorovi različiti od v
     Tada vrednost rastojanja izmedju ta dva cvora ostaje nepromenjena u matrici A (jer d_S(u,t)=d_S'(u,t) ).
  2. Neka je u čvor različit v. Rastojanje čvora u od čvora v se određuje pomoću rastojanja od čvora w, tj.
     d_S (u,v)= d _S' (u,w) +1, tj.
     A[u,v]=A[u,w]+1
  3. A[i,i]=0, jer je rastojanje cvora od samog sebe nula

Vreme izvršavanja opisanog algoritma za problem dimenzije n je T(n), tj.
 

T(n)=T(n-1) + (2n-1)*c1 + c ,     jer iz matrice stabla sa n-1 čvorom se za dodatnih (2n-1)*c1 koraka dolazi do matrice stabla sa n čvorova,
 

gde vrednosti matrice za k-tu vrstu i k-tu kolonu se računaju za const*(2n-1) koraka (matrica A je dimenzije n*n)
dok je c-const vreme potrebno da se nađe čvor w za čvor v

Dakle, T(n)=T(n-1) + (2n-1)*c1 + c=...= T(1) + c2*[2n+2(n-1)+ ... +1] - n*(1+c)=n(n+1)*c2 + n*c3=O (n ²)

     Hip

Hip se može realizovati kao kompletno stablo u kome svaki čvor i njegov naslednik su u relaciji poretka R, gde R može biti relacija <, >,...

Na primer, binarno stablo je kompletno popunjeno ako ima visinu h i 2^h+1-1 cvorova.

Binarno stablo visine h je kompletno ako i samo ako je

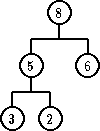
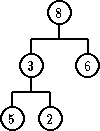
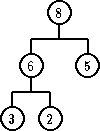
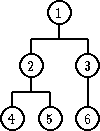
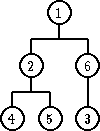
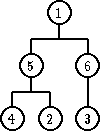
Primer:  Neka  R je relacija  ‘>’ i drvo ima stepen  2. Dakle, heap nije BSP koje ste izučavali ranije, jer svako dete mora u heap-u biti manje od oca. Ne može kao u BSP, da npr. desno dete bude veće.

Hip	Nije hip

1. Primene

 Lista sa prioritetom: dinamički skup čiji elementi se uklanjaju po redosledu veličina, počev od najvećeg.  Na primer, objekat sa najvećim prioritetom se nalazi u korenu heap-a i trivijalno se uzima iz strukture. Ali ako se ukloni koren, tada ostaju dva podstabla i moraju se efikasno spojiti u jedno stablo koje će ponovo imati heap svojstvo.
Korist od upotrebe heap strukture  zasniva se na svojstvu da se moze izvaditi objekat najviseg prioriteta i ubaciti  za O(logn) vremena.

  Heap Sort: od kolekcije elemenata kreira se heap za (O(n)) vremena i potom se uklanjaju elementi iz heap-a, a svako uklanjanje ima složenost proporcionalnu visini heap-a, tj. (O(log n)), te ukupna složenost je (O(n log n))  (donja granica).

REALIZACIJA

1. eksplicitno zadatim stablom

2. vektor, tj. implicitno zadato stablo sa pozicijama 1..n. Koren je na poziciji 1. Na poziciji i > 1 je dete sa pozicije i/2.Na primer, ako niz A je implicitno zadato stablo, onda element A[16] odgovara čvoru čiji predak je čvor pridružen elementu A[8].

Svojstva kompletnog stabla vode do veoma efikasnog mehanizma za memorijsko predstavljanje koristeci n uzastopnih pozicija u nizu, tj. vektoru..

Ako su čvorovi numerisani  počev od 1 u korenu i ako je: levi potomak čvora k na poziciji 2k desni potomak cvora k na poziciji 2k+1 tada osobina 'popunjenosti s leve strane' kompletnog stabla obezbeđuje da heap može da se smesti u uzastopnim pozicijama u vektoru.

Posmatran kao niz, vidi se da se n-ti čvor nalazi na n-tom mestu u nizu.

2. Umetanje elementa u hip

1. dodati čvor u stablo (postaviti ga na mesto sledeceg lista sa desne strane)

   

2. Pomeranje  elemenata od korena do novog čvora sve dok se ne uspostavi svojstvo heap-a.

    

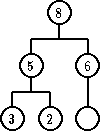
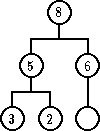
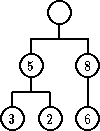
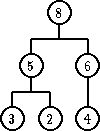
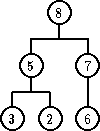
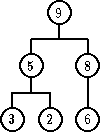
   novi element	4	7	9
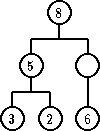
   ažurirano stablo

3. Ubacivanje novog ključa u slobodan čvor

4. Potpuno stablo sa  n čvorova ima dubinu  log n, te je vremenska kompletnost umetanja elementa u hip O(log n), jer u gore opisanom  procesu je potrebno da izvrsimo najvise h izmena korena podstabla sa jednim od njegovih potomaka kako bismo u potpunosti vratili svojstvo gomile. Zato je za brisanje korena iz gomile potrebno O(h), odnosno O(logn) vreme.

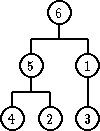
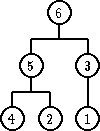
   Ponovo, za ovu proceduru je potrebno O(h), odnosno O(logn) zamena.

2. Uklanjanje elementa iz hipa

1. Ukloniti ključ najvećeg elementa, tj. koren, potom sačuvati ključ najmanjeg elementa, ali ukloniti poslednji čvor, tj. čvor koji je sadržao taj element (npr. vrednost 2)

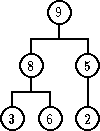
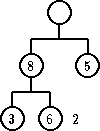
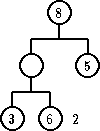
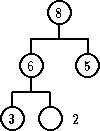
   pre	posle

2. Dok god je sačuvana vrednost manja od deteta upražnjenog čvora, pomeriti najveću vrednost deteta nagore do upražnjenog čvora. Konkretno,  ključ deteta 8 se prekopira u koren, ključ 6 se prekopira u dete korena.

   

3. Zapamćena vrednost se kopira u ključ upražnjenog čvora.

   

4. Složenost O(log n), jer u ovom procesu je potrebno da se izvrši najviše h izmena korena podstabla sa jednim od njegovih potomaka kako bismo u potpunosti važilo heap svojstvo . Zato je za brisanje korena iz heap-a potrebno O(h), odnosno O(logn) vreme.

3. Formiranje hipa (korisno za heap sort) - bottom up pristup

• Ubaciti n elemenata e₁, ..., e_n u potpuno stablo

  

• Za svaki čvor, počev od poslednjih (najnižih) ka korenu, vrši se reorganizacija podstabla u heap tako što se izvrši zamena korena podstabala sa većim detetom sve dok koreni ne budu veći od dece.

  

  

  

  

• Vremenska složenost formiranja heap-a je jednaka sumi složenosti preuređivanja podstabala redom veličine n/2, n/4, n/8, ...

   O(0 * (n/2) + 1 * (n/4) + 2 * (n/8) + + (log n) * 1) = O(n(0 2^-1 + 1 2^-2 + 2 2^-3 + + (log n) 2^{- log n})) = O(n)

  znajući da izraz u zagradi u stvari ima vrednost

    _{k = 1}(k - 1)2^-k =2[ _{k = 1}(k - 1)2^-k] - [ _{k = 1}(k - 1)2^-k] =[ _{k = 1}k2^-k] - [ _{k = 1}(k - 1)2^-k] = _{k = 1}[k - (k - 1)]2^-k

  = _{k = 1}2^-k =1

     Binarna stabla pretrage (BSP)

1. Karakteristike

Savki čvor binarnog stabla ima ne više od dva sina, te je moguće uvesti preslikavanje skupa njegovih sinova u skup {levi, desni}. U BSP ključ svakog čvora veći je od od ključeva svih čvorova levog podstabla, a manji ili jednak je od ključeva svih čvorova desnog podstabla. BSP omogućava efikasno izvršavanje opracija pretrage, umetanja i uklanjanja elementa.

2. Pretraga

BSPpretraga ( drvo, ključ ) 

  IF prazno drvo            return nije_nadjen

  IF ključ == ključ korena  return nadjen

  IF ključ  > ključ korena  BSPpretraga (levo poddrvo,  ključ) 

                            BSPpretraga (desno poddrvo, ključ) 

Vremenska složenost: O(h), h-visina stabla

3. Umetanje

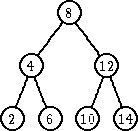
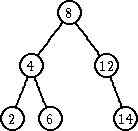
	ubaci 6	ubaci 10

4. Uklanjanje

Čvora koji je list

Ukloniti list

 

 

Uklanjanje čvora stepena 1

 

Ukloniti čvor, a podstablo sa korenom u njegovom sinu se podiže za jedan nivo tako da mu koren bude na mestu uklonjenog čvora

 

Uklanjanje čvora stepena 2

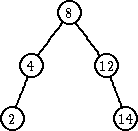
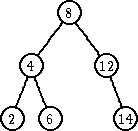
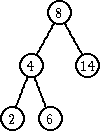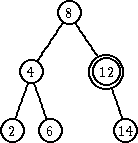
Zameniti čvor koji sadrži  obrisani ključ ili sa čvorom koji poseduje najveći ključ u levom podstablu ili sa čvorom koji ima najmanji ključ u desnom podstablu.

BALANSIRANA STABLA - AVL STABLA (Adelson, Velski, Landis stabla)
 

1. Karakteristike

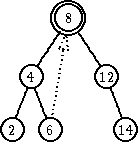
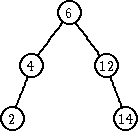
Definicija: AVL stablo je binarno stablo pretrage kod koga je za svaki čvor apsolutna vrednost razlike visina levog i desnog stabla manja ili jednaka od jedan.

Visina stabla je visina njegovog korena, tj. maksimalno rastojanje od korena do nekog čvora..

Visina čvora x je rastojanje od x do najdaljeg potomka.

 Operacije pretrage, umetanja, brisanja nekog elementa obavljaju se za O(log n) vremena, kao kontrast sličnim operacijama u nebalansiranim stablima, kada stablo može da se degeneriše i u sortirani niz.  

2. Visina

Stav: AVL stabla su balansirana, tj. visina im je O(log n).

Dokaz.  Neka N_h označava broj čvorova  AVL stabla visine h

Dakle, ako n je broj čvorova, dobili smo da

Preciznija analiza, zasnovana na Fibonačijevm brojevima (data u knjizi), ukazuje da gornja granica za h je 1.44 log ₂(n + 2), tj. visina AVL stabla je

O(log n).

3. Rotacije

Pri umetanju čvorova u AVL stablo, najpre se pronalazi mesto čvoru tako da bude očuvano svojstvo stabala binarne pretrage o uređenosti ključeva, a potom se u stablo dodaje novi list sa ključem jednakim ključu novog čvora.  Pri tom može da se desi da stablo postane neuravnoteženo, te se primenjuje rotacija.

Razlikuju se

1. 1-struka rotacija (npr. koren levog podstabla podiže se i postaje koren novog stabla, a ostatak stabla se preuređuje tako da stablo ostane BSP stablo, npr. slika LL)

2. 2-struka rotacija i Leva(L) i Desna(R)

LL
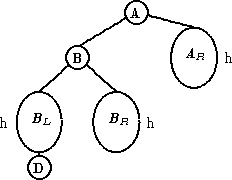
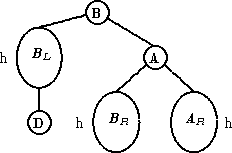
RR
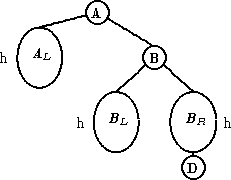
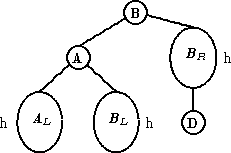
LR
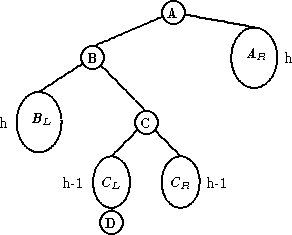
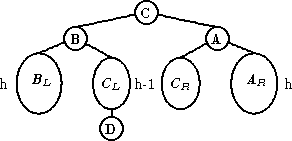
RL
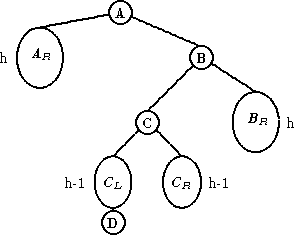
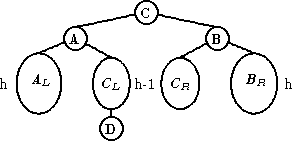
LL & LR LL

4. Uklanjanja

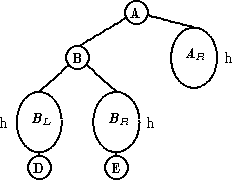
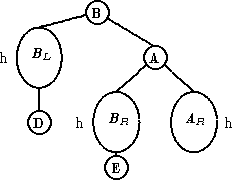
Uklanjanje elementa iz AVL stabla je komplikovanije neko kod običnog BSP stabla, jer je potrebno više rotacija. Na primer, da bi se uravnotežilo Fibonačijevo (potpuno) AVL stablo posle uklanjanja "pogodno" izabranog čvora, nužno je izvršiti h-2 rotacije, gde h je visina stabla.

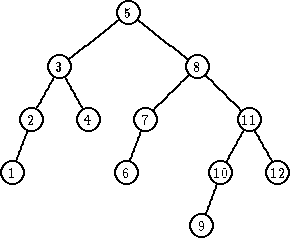Ukloni 4
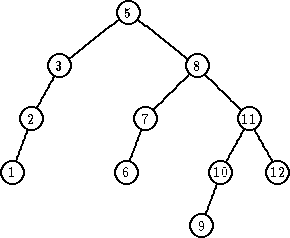
debalans sa 3, LL rotacija sa  ‘2’
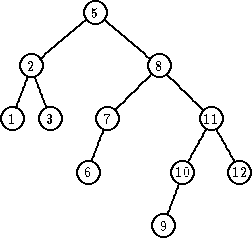
deabalans sa 5, RR rotacija sa ‘8’.

Generalizovana m stabla

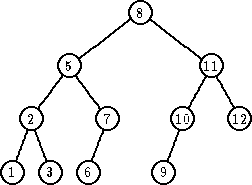
Ako ne važi ograničenja da svaki čvor stabla može da ima samo jedan ključ, tada se može smanjiti  ukupna visina stabla, što je značajno pri pretrazi.

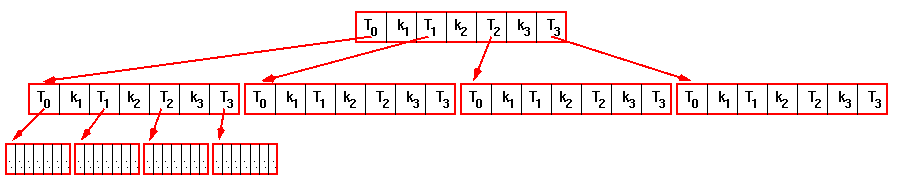
Visina kompletnog m-arnog stabla sa n cvorova je [log_mn].

B-stablo reda m je m-arno stablo u kome su

1. svi listovi su na istom nivou i
2. svi čvorovi, osim korena i listova, imaju bar m/2, a najviše m potomaka. Koren ima bar 2, a najvise m potomaka.

Varijacija B-stabla, poznata kao B+-stablo posmatra sve ključeve u čvorovima koji nisu listovi kao lažne. Svi ključevi su duplirani u listovima, što ima za prednost da ako se svi listovi povežu sekvencijalno, tada se celo stablo može pročitati bez posećivanja čvorova na višim nivoima.

B-stabla

1. Karakteristike

B-stabla su 1972. predložili Bayer i McCreight. Od tada ova stabla su se razvila u više varijanti (B*, B+) i postala jedna od najpopularnijih tehnika za organizaciju indeksnih struktura u datotekama. B-stablo reda m definiše se kao stablo m-arnog pretraživanja sa sledećim svojstvima:

• koren stabla (ako nije list) ima najmanje dva podstabla
• svi čvorovi osim korena i listova imaju najmanje  m/2 podstabala
• listovi imaju najmanje (m - 1)/2  ključeva
• svi listovi su na istom nivou

Drugo svojstvo garantuje da je svaki čvor sem korena barem polupopunjen. Time se poboljšava iskorišćenje prostora kao nedostatak  stabla m-arnog pretraživanja. Isto svojstvo forsira i grananje sa ciljem da broj nivoa bude što manji.

Četvrto svojstvo obezbeđuje balansiranost i garantovane performanse pretraživanja u najgorem slučaju.

B-stablo reda 3	nije B-stablo, jer čvorovi 6, 22 su sa polupounjenosti mogli da imaju popunjenost

2. Umetanja

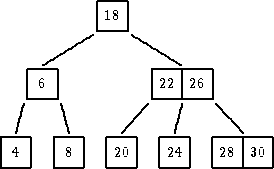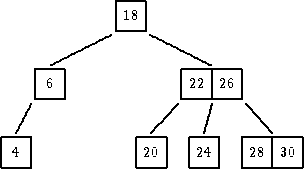
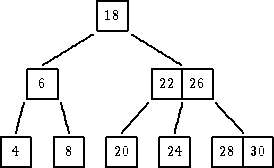
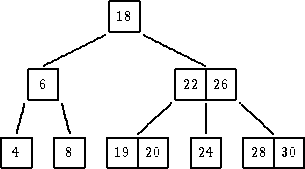
dodati 19: Najpre se pokuša da se novi čvor umetne u list, a najčešće tamo i ostane Konkretno, za 19 se traži list i pozicija u njemu koja mu pripada. Kako u listu sa 20 ima mesta za umetanje, umeće se 19.
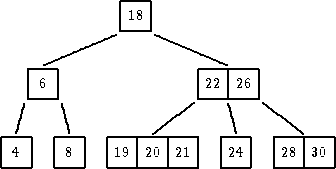
dodati 21: Najpre se pokuša da se novi čvor umetne u list, a najčešće tamo i ostane Konkretno, za 21 se traži list i pozicija u njemu koja mu pripada. Kako u listu sa 20 nema mesta za umetanje, jer list u koji treba umetnuti več ima m-1 ključ, onda dolazi do preloma (split) lista..
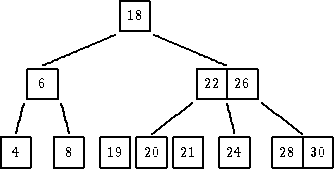
Alocira se prostor za novi čvor 19, a potom 21
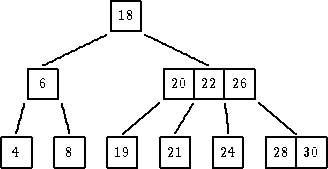
Pravilo: Formira se rastuće sortiran niz od m=3 ključa, tako što se ključevi od 1..m/2-1 zadrze u starom listu, kljuc sa pozicije m/2 ide u roditeljski list, a kljucevi do Km idu u eventualno nov list ili ako roditeljski cvor nije pun, onda prima srednji kljuc (ovde je to 22) sa donjeg nivoa.
Dakle, 19, 21 idu u naslednike cvora 20.
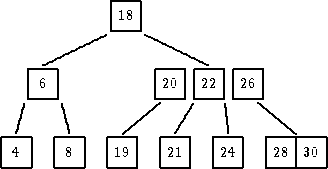
Cvor 22 se penje navise.

3. Uklanjanja

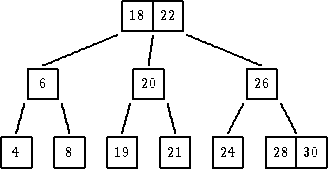
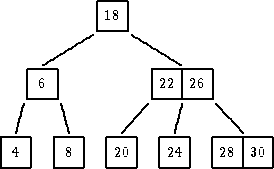
ukloniti 26

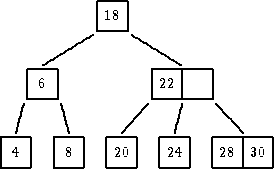
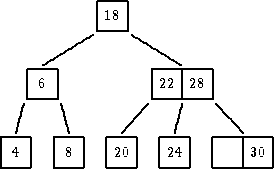
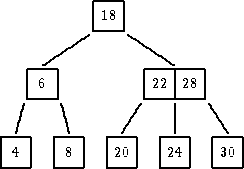
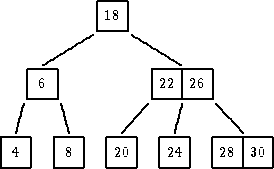
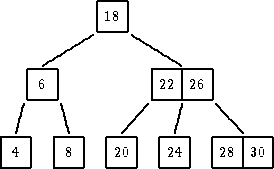
ukloniti 22

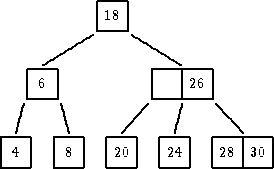
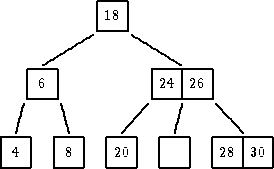
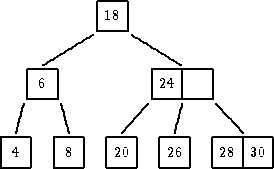
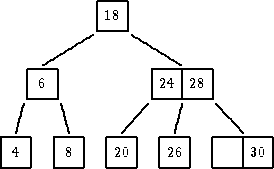
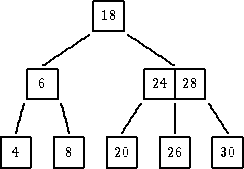
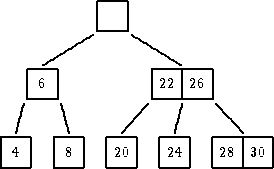
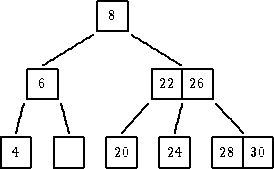
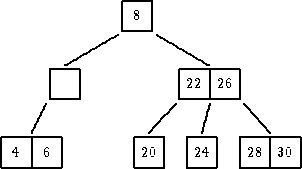
ukloniti 18

Crveno-crna stabla

1. Karakteristike

Osim AVL stabla, postoje i druga "skoro balansirana stabla" sa relaksiranim kriterijumima koja garantuju logaritamsku performansu. Crveno-crna stabla imaju nekoliko interesantnih osobina:

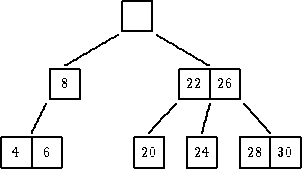
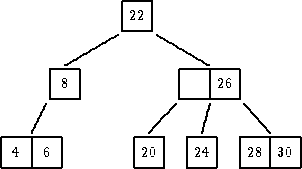
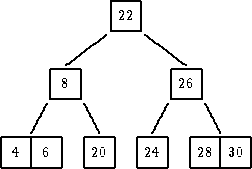
• svaki  čvor je crn ili crven

• ako čvor je crven, oba njegova sina su crna

• svaki prost put od korena do lista sadrži isti broj crnih čvorova

• nijedna putanja od korena do lista nije više od dva puta duža od bilo koje druge

  Treća osobina obezbeđuje relaksiranu balansiranost stabla i značajna je za logaritamske performanse stabla.

  Četvrta osobina daje grantovane performanse stabla O(log n) u n ajgorem slučaju.

  Crveno-crno stablo je binarno stablo pretrazivanja sa jos jednim dodatnom informacijom za svaki cvor: bojom, koja je ili crvena ili crna. Ta dodatn ainformacija se može kodirati sa 1 botom.  Takodje je neophodno vodti racuna o roditelju svakog cvora, tako da bi struktura cvora crveno-crnog stabla mogla biti:

  struct t_red_black_node {
  
      enum { red, black } colour;
  
      void *item;
  
      struct t_red_black_node *left,
  
                       *right,
  
                       *parent;
  
      }
  
  

  Tokom ovog razmatranja, NULL cvorove koji zavrsavaju stablo smatracemo listovima i obojene u crno.

   

Lema

Crveno-crno stablo sa n unutrasnjih cvorova ima visinu najvise 2log(n+1).

Sada se vidi zasto je crveno-crno stablo dobro stablo za pretrazivanje: ono se uvek moze pretraziti u O(log n) koraka.

Kao i kod hipa, dodavanja i brisanja iz crveno-crnog stabla remete crveno-crne osobine, tako da ih je potrebno popravljati. Da bismo ovo uradili, neophodno je da pogledamo nekoliko operacija na crveno-crnim stablima.

Rotacija

Rotacija je lokalna operacija u stablu pretrazivanja koja očuvava in-order poredak ključeva. Primetimo da u oba stabla, in-order obilazak daje:   A x B y C

Operacija leve rotacije može da se kodira na sledeći način:

left_rotate( Tree T, node x ) {

    node y;

    y = x->right;

    /* Pretvoriti levo podstablo cvora y u desno podstablo cvora x */

    x->right = y->left;

    if ( y->left != NULL )

        y->left->parent = x;

    /* Novi roditelj cvora y je bivsi roditelj cvora x */

    y->parent = x->parent;

    /* Roditelj mora da pokazuje na cvor y umesto na cvor x */

    /* Najpre proverimo da li se nalazimo u korenu - tada nema roditelja! */

    if ( x->parent == NULL ) T->root = y;

    else

        if ( x == (x->parent)->left )

            /* cvor x je bio sa leve strane svog roditelja */

            x->parent->left = y;

        else

            /* inace je cvor x morao da bude sa desne strane */

            x->parent->right = y;

    /* Konacno, stavimo cvor x sa leve strane cvora y */

    y->left = x;

    x->parent = y;

    }

Dodavanje

Dodavanje je relativno slozeno i ukljucuje veliki broj slucajeva. Primetimo da dodavanje novog cvora x u crveno-crno stablo pocinjemo na isti nacin kao sto bismo to uradili sa bilo kojim binarnim stablom, koristeci funkciju tree_insert.  Taj postupak je opisan gore pri dodavanju čvora u binarno stablo pretrage.

Novi čvor se oboji u crvenu boju. Ali, to možda remeti crveno-crne osobine. Da bi se to otklonilo, vrše se izvesne izmene. Izmene se obavljaju u ,  glavnoj petlji kada se penjemo uz stablo ka korenu, dok ne oporavimo crveno-crne osobine. Pri penjanju se uvek nalazimo u crvenom čvoru, a postupak se prekida onog trenutka kada je roditelj crvenog čvora u kom se nalazimo, zapravo crn.

rb_insert( Tree T, node x ) {

    /* Dodavanje u stablo na uobicajen nacin */

    tree_insert( T, x );

    /* Sada oporavi crveno-crne osobine */

    x->colour = red;

    while ( (x != T->root) && (x->parent->colour == red) ) {

       if ( x->parent == x->parent->parent->left ) {

           /* Ako je roditelj x sa leve strane, tada je y desni ujak cvora x */

           y = x->parent->parent->right;

           if ( y->colour == red ) {

               /* slucaj 1 - promeni boje */

               x->parent->colour = black;

               y->colour = black;

               x->parent->parent->colour = red;

               /* Pomeri x nagore kroz stablo */

               x = x->parent->parent;

               }

           else {

               /* y je crni cvor */

               if ( x == x->parent->right ) {

                   /* a x je sa desne strane */

                   /* slucaj 2 - pomeri x nagore i rotiraj */

                   x = x->parent;

                   left_rotate( T, x );

                   }

               /* slucaj 3 */

               x->parent->colour = black;

               x->parent->parent->colour = red;

               right_rotate( T, x->parent->parent );

               }

           }

       else {

           /* ponoviti "if" deo sa izmenjenim "right" i "left" */

       }

    /* Oboji koren u crno */

    T->root->colour = black;

    }

2. Umetanja

LLr, leva rotacija, jer naslednici levog čvora B nisu oba crna, tj. nije levi naslednik. Iz B se penjemo ka korenu sve dok smo u crvenom čvoru. Stajemo kod A i on se proglasi za crveni, a njegovi sinovi za crni.
LRr, LLr, levodesna rotacija, jer naslednici levog čvora B nisu oba crna, tj. nije desni naslednik C. Iz B se penjemo ka korenu sve dok smo u crvenom čvoru. Stajemo kod A i on se proglasi za crveni, a njegovi sinovi za crni.

Formiranje crveno-crnog stabla

Dodavanje novog čvora x u crveno-crno stablo počinjemo na isti nacin kao sto bismo to uradili sa bilo kojim binarnim stablom, koristeci funkciju tree_insert.  Taj postupak je opisan gore pri dodavanju čvora u binarno stablo pretrage.

Novi čvor se oboji u crvenu boju. Ali, to možda remeti crveno-crne osobine. Da bi se to otklonilo, vrše se izvesne izmene. Izmene se obavljaju u ,  glavnoj petlji kada se penjemo uz stablo ka korenu, dok ne oporavimo crveno-crne osobine. Pri penjanju se uvek nalazimo u crvenom čvoru, a postupak se prekida onog trenutka kada je roditelj crvenog čvora u kom se nalazimo, zapravo crn.

dodati 1
dodati 2
dodati 3	RR rotacija zbog balansiranosti, oko desnog poddrveta 2-3
dodati 4	kod čvora 3 narušeno boja zbog naslednika
dodati 5	RR rotacija zbog balansiranosti oko desnog poddrveta 3-4-5	nužno je bojenje desnog poddrveta

Liste povezanosti - grafovi

Osnovni pojmovi

Graf

Usmeren graf

Grane usmerenog grafa su uređeni parovi čvorova i redosled dva čvora koje povezuje grana je bitan.

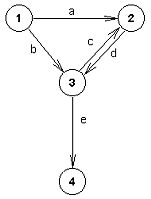
Slika 1
 
 

Neusmeren graf

Graf sa slike 2 je neusmeren i čvorovi 2 i 3 su povezani granama b i c.
 

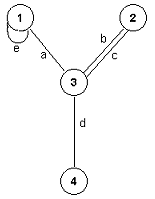
Slika 2

  Specijalan primer grafa jeste stablo koje predstavlja povezan graf bez ciklusa, tj. svi čvorovi su povezani među sobom i nema cikličnih puteva kroz stablo. Ako je na stablu potrebno definisati hijerarhiju, onda se sve grane mogu usmeriti od "korena". Takva stabla se nazivaju korenska stabla. Koren je poseban izdvojen čvor stabla, a listovi stabla su čvorovi koji nemaju naslednike.

Stablo ili drvo

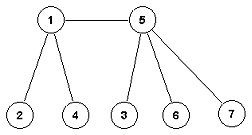
Uobičajena su dva načina predstavljanja stabla:

    matricom povezanosti

    listom povezanosti.

Matrica povezanosti grafa G je kvadratna matrica A reda n (gde |V|=n), gde A[i,j]=1 ako postoji grana od čvora v_i  do čvora v_j. Ostali elementu su nule.  Ako graf G je neusmeren, matrica je simetrična. Ako je broj grana u G mali, onda većina elemenata matrice će biti nula, ali će ona i dalje zauzimati prostor veličine n*n, sto je nedostatak ovog tipa reprezentacije ako se koristi za retke grafove.

Lista povezanosti pak omogućuje da se ne vrši eksplicitno predstavljanje nepostojećih grana. Svakom čvoru pridružuje se povezana lista koja sadrži sve grane ka susednim čvorovima. Svaki element liste (tj. jednodimenzionog niza) sadrži indeks čvora grafa G i pokazivač na njegovu listu čvorova. Ako G je statički graf (tj. ne vrše se umetanja, brisanja), onda se za realizaciju liste povezanosti koristi niz dužine |V|+|E|, gde prvih |V| elemenata su pridruzeni cvorovima grafa, a vrednost na poziciji  j pridruzena cvoru  v_j sadrzi indeks pocetka spiska čvorova susednih čvoru  v_j.

Lista povezanosti

	7  9 10  -  -  -  2  3  4  5  6  1  2  3  4  5  6  7  8  9 10 11
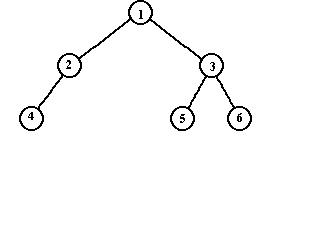1. član liste je 7, te na 7. poziciji je početak čvorova koji su vezani sa čvorom 1, tj. korenom.
2. član liste je 9, te na 9. poziciji je početak čvorova koji su vezani sa čvorom 2.

Hash tabele

Tabele sa direktnim adresiranjem

Neka u skupu od n elemenata, ključevi članova skupa jesu jedinstveni celi brojevi u intervalu (1,m), gde je m >= n. Tada se elementi mogu smestiti u tabelu sa direktnim adresiranjem T[m], gde je Ti ili prazno polje ili sadrži jedan element iz polaznog skupa. Pretrazivanje tabele sa direktnim adresiranjem je  O(1) operacija, jer za ključ k pristupa se polju Tk, ako polje sadrži element, rezultat rada je taj element ako je polje prazno, rezultat rada je NULL. Ovde postoje dva ograničenja: ključevi moraju da budu jedinstveni i opseg ključeva mora da bude ograničen.

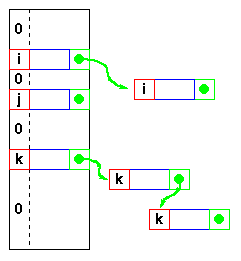
Ukoliko ključevi nisu jedinstveni, tada se može kreirati skup od m povezanih listi tako da u polja tabele direktnog adresiranja budu smeštene adrese glava ovih listi. Vreme za nalaženje elementa koji odgovara ulaznom kljuću je i dalje O(1) - to je element sadržan u glavi odgovarajuće liste. Medjutim, ako elementi skupa imaju još neku osobinu po kojoj se razlikuju (sem ključa), i ako je maksimalan broj duplih ključeva ndupmax, tada traženje određenog elementa traje O(ndupmax) koraka. Ako su duplikati retki, tada je ndupmax mnogo manje od n i tabela sa direktnim adresiranjem će dati dobre performanse. Ali ako je ndupmax istog reda veličine kao i n, tada traženje određenog elementa traje O(n) koraka i korišćenje strukture stabla bi bilo mnogo efikasnije.

Opseg ključeva određuje veličinu tabele direktnog adresiranja, koja može da bude suviše velika da bi bila praktična. Na primer, malo je verovatno da cete u sledecih par godina moci da koristite tabelu direktnog adresiranja za smestanje elemenata koji kao kljuceve imaju proizvoljne 32-bitne cele brojeve!

Direktno adresiranje se lako uopstava na slucaj kada postoji funkcija

koja svaku vrednost kljuca k preslikava u interval (1,m). U ovom slucaju, element sa kljucem k smestamo u T[h(k)] (umesto u T[k]) i jos uvek mozemo da pretrazujemo u O(1) koraka kao i ranije.

Jedan jednostavan princip je da se svi sudari povezu u listu koja se prikaci na odgovarajuce polje. Ovako se moze rukovati neogranicenim brojem sudara i ne zahteva se unapred podatak o tome koliko elemenata se nalazi u skupu. Nedostatak je isti kao i kod implementacije skupa pomocu povezanih listi, umesto pomocu nizova: povezane liste traze vise prostora i, u manjem stepenu, vremena.

Re-hashiranje

Princip re-hashiranja koristi jos jednu hash funkciju kada dodje do sudara. Ako ponovo nastane sudar adresa, onda re-hashiramo dok se ne nadje prazno polje u tabeli. Re-hash funkcija moze da bude ili sasvim nova funkcija ili ponovna primena originalne funkcije. Sve dok se funkcije primenjuju na kljuc u istom poretku, trazeni kljuc ce uvek moci da se nadje. Linearni preskok Jedna od najjednostavnijih re-hash funkcija je +1 (ili -1), tj. kad nastane sudar, pogledaj u susedno polje tabele. Nova adresa se racuna ekstremno brzo i moze biti ekstremno efikasna na modernim procesorima zahvaljujuci efikasnoj upotrebi kes memorije ().

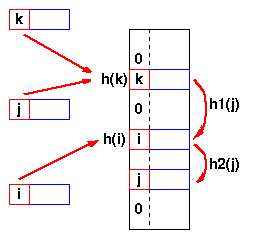h(j)=h(k), pa se koristi sledeca hash funkcija h1. Nastaje i drugi sudar, pa se koristi sledeca hash funkcija h2.

Nagomilavanje

Linearni preskok je sklon fenomenu nagomilavanja. Re-hashirani elementi iz jednog polja zauzimaju blok polja u tabeli koji "raste" prema poljima koja zauzimaju drugi kljucevi. Ovo pogorsava problem sudara i broj re-hashiranih elemenata moze da postane veliki.

Kvadratni preskok

Bolje ponasanje se obicno dobija sa kvadratnim preskokom, gde sekundarna hash funkcija zavisi od re-hash indeksa:

kod i^-tog re-hashiranja. (Slozenija funkcija od i se takodje moze koristiti.) Posto kljucevi, koji se preslikavaju u istu vrednost, slede isti niz adresa, kvadratni preskok pokazuje sekundarno nagomilavanje. Medjutim, sekundarno nagomilavanje je mnogo manje ozbiljno od nagomilavanja prouzrokovanog linearnim preskokom.

Re-hashing principi koriste originalno alociran prostor za tabele i stoga izbegavaju nedostatke povezanih listi, ali zahtevaju da se broj elemenata koje treba smestiti zna unapred.

Ipak, sudareni elementi se smestaju u polja u koja se drugi elementi preslikavaju direktno, tako da se potencijal za visestruke sudare povecava kako se tabela popunjava.

Oblast prelivanja

Ovaj princip deli pre-alociranu tabelu u dve oblasti: primarnu oblast u koju se preslikavaju kljucevi i oblast za sudare, koja se obicno zove oblast prelivanja.

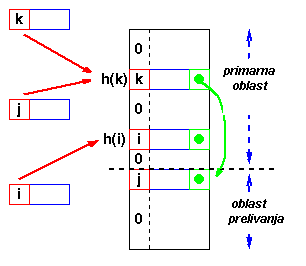Kada dodje do sudara, za novi element se koristi polje u oblasti prelivanja, a u primarnom polju se napravi pointer kao u povezanoj listi. Ovo je u sustini isto kao ulancavanje, osim sto je oblast prelivanja pre-alocirana i stoga moguce brza za pristup. Kao i sa re-hashiranjem, maksimalan broj elemenat mora biti poznat unapred, ali u ovom slucaju, moraju se proceniti dva parametra: optimalna velicina primarne oblasti i oblasti prelivanja.

Naravno, moguce je dizajnirati sisteme sa visestrukim oblastima prelivanja, ili sa mehanizmom za rukovanje sudarima u oblasti prelivanja, koja daju fleksibilnost bez gubitka prednosti oblasti prelivanja.

Rezime: organizacija hash tabele

Izbor dobre hash funkcije h(k) je osnovni problem kod korišćenja hash tabela za pretraživanje. Funkcija h bi trebalo da raspodeli elemente našeg skupa što je moguće ravnomernije u polja hash tabele. Ključni kriterijum je da bi broj sudara trebalo da bude što manji.

Ako je P(k) verovatnoća da se ključ k pojavljuje u nasem skupu, tada bi, ako postoji m polja u nasoj hash tabeli, uniformna hash funkcija h(k) osigurala da:

Ponekad je ovo jednostavno obezbediti. Na primer, ako su kljucevi slucajno rasporedjeni u intervalu (0,r], tada funkcija

obezbedjuje ravnomerno hashiranje.

Preslikavanje kljuceva u prirodne brojeve

Vecina hash funkcija ce najpre preslikati kljuceve u neki skup prirodnih brojeva, recimo (0,r]. Postoji mnogo nacina da se ovo uradi, na primer, ako je kljuc niz ASCII znakova, mozemo jednostavno da saberemo ASCII brojeve znakova po modulu 255 da bismo dobili broj u intervalu [0,255) - ili mozemo na njih da primenimo xor, ili ih mozemo sabirati u parovima po modulu 2¹⁶-1, or ...

Posto smo preslikali kljuceve u skup prirodnih brojeva, imamo puno mogucnosti za hash funkciju.

1. Koristiti funkciju mod:

   h(k) = k mod m.

   Pri koriscenju ovog metoda, izbegavaju se odredjene vrednosti m. Obicno se izbegavaju stepeni dvojke, jer k mod 2^b jednostavno daje b najnizih bitova broja k. Osim u slucaju da znamo da su svih 2^b mogucih vrednosti najnizih bitova podjednako verovatne, ovo ne bi bio dobar izbor, jer se neki bitovi kljuca ne koriste u hash funkciji.

   U principu, prosti brojevi koji su bliski stepenima dvojke izgledaju kao povoljan izbor za m.

   Na primer, ako imamo 4000 elemenata, i izabrali smo organizaciju sa oblascu prelivanja, ali zelimo da sto je vise moguce smanjimo verovatnocu sudara, tada bismo mogli da izaberemo m = 4093. (4093 je najveci ceo broj manji od 4096 = 2¹².)

2. Koristiti metod mnozenja:
   • Pomnoziti kljuc konstantom A, 0 < A < 1,
   • Ostaviti samo razlomljeni deo proizvoda,
   • Pomnoziti ovu vrednost sa m.

   Prema tome, hash funkcija je:

    

   h(k) = floor(m * (kA - floor(kA)))

   U ovom slucaju, vrednost m nije kriticna i obicno se bira stepen dvojke, tako da mozemo da dobijemo sledecu efikasnu proceduru na vecini racunara:

   • Izabrati m = 2^p.
   • Pomnoziti w bita kljuca k sa floor(A * 2^w) da bi se dobio proizvod sa 2w bita.
   • Ostaviti samo p najznacajnijih bitova donje polovine ovog proizvoda.

     Stoga

      

     A = (sqrt(5)-1)/2 = 0.6180339887

     je veoma dobar izbor (prema Knuth, "Sorting and Searching", 3. tom u seriji "The Art of Computer Programming").

3. Koristiti univerzalno hashiranje:

   Oni skloni kontraprimerima  bi uvek mogli da izabere kljuceve tako da se oni svi preslikavaju u isto polje hash tabele, prouzrokujuci prosecno O(n) vreme za pretrazivanje. Univerzalno hashiranje pokusava da izbegne ovu situaciju birajuci hash funkciju slucajno iz skupa hash funkcija. Ovo smanjuje verovatnocu da ce hash funkcija dati lose ponasanje i u proseku daje dobre performanse.

Primene stabla (više u delu o grafovima)

 1. Predstavljanje aritmetičkih izraza

Ako se posmatra izraz zadat u infiksnoj notaciji, uočava se da se on može prirodno predstaviti binarnim stablom kod koga su čvorovima grananja pridruženi operatori, dok levo i desno podstablo predstavljaju složene operande (podizraze). Listovi stabla predstavljaju elementarn operande - promenljive i konstante. Obilaskom ovakvog stabla preorder/postorder obilasku dobija se prefiksna/postfiksna varijanta aritmetickog izraza.

Preko stabala se moze proveriti i slicnost struktura dva izraza. Proveri se slicnost strukture stabala, s tim sto čvorovi koji predstavljaju komutativne operatore (+,-,...) ne prave razliku između levogi desnog podstabla.

Sa izrazima se mogu vršiti i ostale korisne manipulacije. Diferenciranje izraza se obavlja pomoću obilaska stabla na postorder način. Najpre se difrenciraju prosti operandi, a potom izrazi po pravilima diferenciranja za odgovarajuće operande sve dok se ne obradi čitav izraz.

2. Stabla odlučivanja

Pri rešavanju problema često se pojavljuju situacije u kojima treba na osnovu nekog uslova ili stanja doneti odluku u kom pravcu nastaviti rešavanje, čime se sužava broj mogućih ishoda. Ovakav način rešavanja se može pogodno modelirati stablom odlučivanja. Često se koristi kada treba izvesti što manji broj merenja da bi se detektovali defektni objekti u nekoj kolekciji (npr. lažne osobe, lakši novčići, teže kuglice,...). Grane i čvorovi predstavljaju uslove i akcije koje se obavljaju, pri čemu gornji deo stabla predstavljaju pravila koja odgovaraju if naredbama sa složenim uslovima, a listovi stabla sadrže rezultat radsa prostog pravila, tj. rezultat proste if naredbe.

3. Stabla igara

Stabla se često koriste u realizaciji raznih igara koje se igraju na računaru kao što su šah, iks-oks,... U takvim igrama za tablom postoje dva igrača koji naizmenično povlače poteze, a stanje igre se predstavlja pozicijom na tabli. Neka postoji konačan broj ovakvih poteza. Za takvu igru se može konstruisati stablo igre gde svaki čvor predstavlja jednu poziciju na tabli. Koren predstavlja početnu poziciju, a listovi stabla predstavljaju završne pozicije: pobede, poraza, nerešenog ishoda. Parni nivoi stabla predstavljaju pozicije u kojima potez vuče prvi igrač, a neparni pozicije u kojima vuče drugi igrač. Izbor poteza u nekoj pozicviji zasniva se od pricene vrednosti pozicije. Pridruživanje vrednosti počinje od listova koje dobijaju vrednosti 1, 0, -1 ako završna pozicija završava, pobedom, nerešeno, porazom. Zatim se vrednosti propagiraju od listova ka korenu. Postoje i tehnike odsecanja koje omogućavaju da se veliki delovi stabla izbace iz razmatranja, jer ne mogu dati minimum ili maksimum na izvesnom nivou.

4. Tabela simbola

5. Predstavljanje prioritetnog reda

Jelena Grmuša

Primene računara