1.
Za graf koji ima n čvorova i m grana odrediti potreban prostor za predstavljanje grafa matricom povezanosti ili listom povezanosti.
|
|
matrica |
lista |
|---|---|---|
|
usmereni |
n*n |
n+m |
|
neusmereni |
n*(n+1)/2 (gornji trougao) |
n+2m |
2.
Za graf koji ima n čvorova i m grana odrediti da li je predstavljanje grafa pogodnije matricom povezanosti ili listom povezanosti u sledecim situacijama:
1. provera da li grana (x, y) pripada grafu
2. redak graf (m<<n*n)
3. dodavanje ili brisanje grana iz grafa
4. markiranje grana
5. obilazak grafa
|
Opis situacije za graf sa n čvorova i m grana |
Pogodna struktura podataka |
|
provera da li grana (x, y) pripada grafu |
matrica povezanosti (brže, zbog direktnog pristupa ocitavanjem, tj. O(1) nasuprot O(duž.liste)) |
|
retki grafovi |
lista povezanosti (manje memorije tj. (m+n) nasuprot n*n npr. usmeren graf, n=5 000, i samo m=10 000 grana matrica: 25 000 000 elemenata. ) |
|
uklanjanje grana |
matrica povezanosti ( O(1) nasuprot O(duz.liste)) |
|
za dati čvor naći sve neposredne susede, tj. druge čvorove koji su povezani granom sa datim čvorom, |
lista povezanosti (nasuprot matrici povezanosti koja zahteva da se proveri ceo red u matrici). |
|
obeležavanje ili numeracija grana |
lista povezanosti(O(n+m) nasuprot O(n*n) da bi se locirale grane) |
|
obilazak grafa |
lista povezanosti (brže, tj. O(m+n) nasuprot O(n*n)) |
3.
Neka je G=(V,E) stablo sa n čvorova. Cilj je formirati simetričnu kvadratnu matricu A reda n, čiji elemenat (i,j) je jednak rastojanju između čvorova vi i vj. Konstruisati algoritam složenosti O (n 2) koji rešava ovaj problem ako je stablo zadato listom povezanosti.
|
matrica rastojanja A |
... |
i |
... |
n |
|
... |
|
|
|
|
|
j |
|
dS (vi,vj) |
|
|
|
... |
|
|
|
|
|
n |
|
|
|
|
Koristimo induktivni pristup:
rešenje je jednostavno za stablo sa jednim ili dva čvora
neka je pretpostavka da se zna rešiti problem za stablo sa n-1 čvorova
POLAZNE PRETPOSTAVKE I OZNAKE:
Neka je dato stablo S sa n čvorova i
neka v je list tog stabla i
neka w je jedini čvor susedan sa v (po definiciji lista u binarnom stablu, jasna je njegova egzistencija i jedinstvenost).
POSTUPAK
Uklanjanjem lista v iz S dobija se stablo S' sa n-1 čvorova, za koje se u O (n 2) koraka može izračunati matrica A svih rastojanja (sledi iz induktivne hipoteze).
Neka su u, t proizvoljan
čvorovi različiti od v
Tada vrednost
rastojanja izmedju ta dva cvora ostaje nepromenjena u matrici A
(jer dS(u,t)=dS'(u,t) ).
Neka je u čvor
različit v. Rastojanje čvora u od čvora
v se određuje pomoću rastojanja od čvora w,
tj.
dS (u,v)= d S' (u,w) +1, tj.
A[u,v]=A[u,w]+1
A[i,i]=0, jer je rastojanje cvora od samog sebe nula
Vreme izvršavanja opisanog algoritma za problem dimenzije n
je T(n), tj.
T(n)=T(n-1) + (2n-1)*c1 , jer iz matrice
stabla sa n-1 čvorom se za dodatnih (2n-1)*c1 koraka
dolazi do matrice stabla sa n čvorova,
gde vrednosti matrice za k-tu vrstu i k-tu kolonu se računaju
za const*(2n-1) koraka (matrica A je dimenzije n*n)
Dakle, T(n)=T(n-1) + (2n-1)*c1 =...= T(1) +
c2*[2n+2(n-1)+ ... +1] - n*(c)=n(n+1)*c2 + n*c3=O (n 2)
Obilazak zapocinje iz proizvoljnog zadatog cvora r, korena pretrage u dubinu. Koren se označava kao posecen. Zatim se bira proizvoljni neoznaceni čvor r1, susedan sa r, pa se iz čvora r1 rekurzivno startuje pretraga u dubinu.
Iz nekog nivoa rekurzije izlazi se kad se naidje na cvor v kome su svi susedi (ako ih ima) vec oznaceni. Ako su u trenutku zavrsetka pretrage iz r1, svi susedi cvora r oznaceni, onda se pretraga za cvor r zavrsava.
U protivnom, bira se sledeci proizvoljni neoznaceni sused r2 cvora r, izvrsava se pretraga polazeci od r2, itd.
Pretraga grafa uvek se vrsi sa nekim ciljem. Da bi se razlicite aplikacije uklopile u pretragu u dubinu, poseti cvora ili grane pridruzuju se dve vrste obrade: ulazna obrada i izlazna obrada.
Ulazna obrada vrsi se u trenutku oznacavanja cvora.
Izlazna obrada vrsi se posle povratka nekom granom, ili kad se otkrije da neka grana vodi vec oznacenom cvoru.
Ulazna i izlazna obrada zavise od konkretne primene DFS.
Algoritam DFS(G; v);
Ulaz: G = (V;E) (neusmereni povezani graf) i v (cvor grafa G).
Izlaz: zavisi od primene.
begin
oznaci v;
izvrsi ulaznu obradu na v; //ulazna obrada zavisi od primene DFSg
for sve grane (v;w) do
if w je neoznacen then DFS(G;w);
izvrsi izlaznu obradu za (v;w) //izlazna obrada zavisi od primene DFS
//ona se ponekad vrsi samo za grane ka novooznacenim cvorovima
end
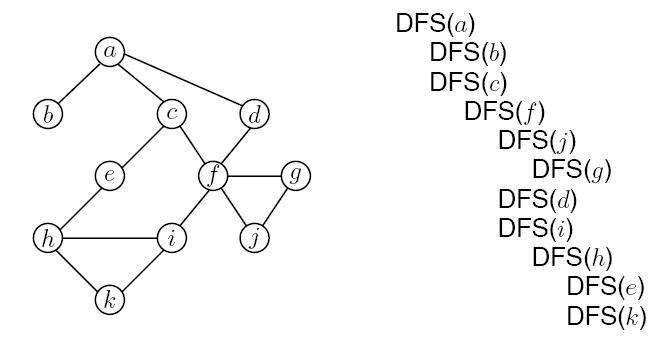
Primer DFS pretrage

4. Implementirati DFS algoritam za obilazak grafa G=(V,E) koji je zadat matricom povezanosti (npr. a[i][j]=1, ako postoji grana (i,j),inace a[i][j]=0) tako da ispise cvorove u redosledu obilaska.
/* DFS implementacija u programskom jeziku C za graf dat matricom povezanosti */
#include <stdio.h>
#define MAX 10 /*maksimalan broj cvorova*/
void poseti(int x, int a[][MAX], int n, int m[]);
/*obilazak grafa sa n cvorova zadatog matricom a pocev od neposecenog cvora x;
pri obilasku u nizu markiranih cvorova m, vrednost clana m[x] ce postati 1, kad se poseti cvor x*/
void DFS(int a[][MAX], int n); /*DFS obilazak grafa G sa n cvorova zadatog matricom povezanosti a*/
void ucitaj_matricu(int a[][MAX], int n); //ucitavanje grana grafa sa stdin
main()
{int a[MAX][MAX];
int n; //broj cvorova grafa
printf("\nUnesite broj cvorova grafa: ");
scanf("%d", &n);
ucitaj_matricu(a,n);
DFS(a, n);
}
void poseti(int x, int a[][MAX], int n, int m[])
{
int y; //cvor koji je u grafu potencijalni sused cvora x
printf(" %d ", x); //stampa se neposeceni cvor od kog krece nova poseta DFSom
m[x]=1; //markira se cvor x kao posecen
/*ako postoji susedni cvor y koji nije markiran(m[y]=0), rekurzivno se poziva poseti za y */
for (y=0; y<n; y++)
if( m[y]==0 && a[x][y]==1) poseti(y, a, n, m);
}
void DFS(int a[][MAX], int n)
{
int x, m[MAX]; //cvor grafa x, niz markiranih (posecenih) cvorova m
for (x=0; x<n; x++) m[x]=0; //na pocetku su svi cvorovi neposeceni
for (x=0; x<n; x++)
if (m[x]==0) poseti(x, a, n, m); //ako x nije posecen, pokrenuti posetu iz x
}
void ucitaj_matricu(int a[][MAX], int n)
{
int i, j;
for (i=0; i< n; i++)
for(j=0; j<n; j++) a[i][j]=0;
printf("\nUnesite grane grafa u obliku x,y. Zavrsite sa EOF\n");
while (scanf("%d,%d", &i, &j) != EOF) a[i][j]=1;
}
SLOZENOST (videti predavanja):
Neka |V|=n, |E|=m.
U potprogramu DFS, prvi for ciklus za obelezavanje cvorova se izvrsi O(n) puta.
Da bi se ocenilo vreme izvrsavanja drugog for ciklusa, potrebno je odrediti vreme poziva poseti(x)
za svaki neposeceni cvor x.
Uocava se da se poseti(x) poziva tacno jednom za svaki cvor x.
Vreme izvrsavanja poseti(x) zavisi od broja suseda za cvor x.
Ako je broj suseda od x oznacimo sa d(x), onda se telo for ciklusa u potprogramu poseti
izvrsava d(x) puta.
Ukupno vreme za izvrsavanje poseti(x) je O(1) + O(d(x)), jer kad d(x)=0, onda je potrebno
O(1) operacija u potprogramu poseti.
Kako se poseti(x) poziva tacno jednom za svaki cvor x, ukupno vreme svih tih poziva za sve cvorove x iz skupa V
u DFS je:
∑1..n O(1+d(xi))=
O (∑1..n (1+d(xi) ) )=
O( ∑1..n1 + ∑1..n d(xi) ) =
O(n+2m) = O(n+m)= O(|V|+|E|)
5. Dat je na slici neusmeren graf G=(V,E). Primeniti DFS obilazak i skicirati stablo DFS pretrage
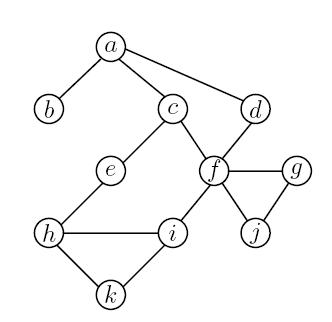
RESENJE:
 |
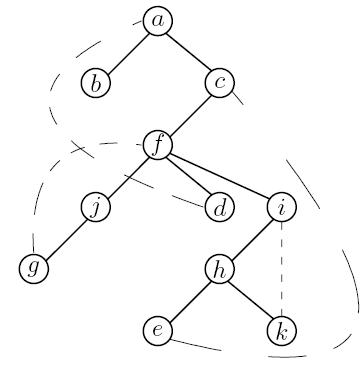 |
6. Na graf iz prethodnog zadatka primeniti DFS obilazak i za svaki čvor iz V prikazati početno vreme/završno vreme. Početno vreme predstavlja vreme prvog nailaska na čvor u DFS algoritmu. Završno vreme se odnosi na vreme kada su obrađeni svi susedi čvora. Polazni čvor je čvor A.
RESENJE:
 |
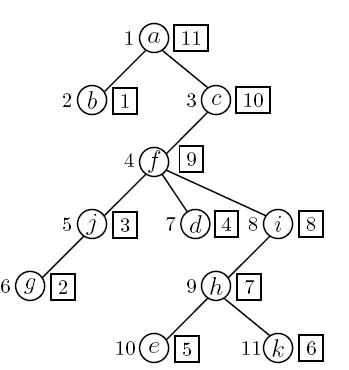
|
7.
|
|
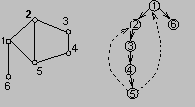
Dat je usmeren graf na slici. Primeniti DFS obilazak, skicirati DFS stablo i za svaki čvor iz V prikazati početno vreme/završno vreme. Klasifikovati bar jednu granu stabla, direktnu granu, povratnu i poprečnu granu. |
Podsećanje:
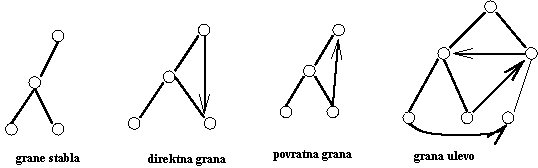
DFS pretraga se vrsi i kod usmerenih grafova sličnim mehanizmom kao i kod neusmerenih grafova, ali usmerena DFS stabla imaju drugačije osobine, tj. postoji četiri tipa grana:
grane stabla
povratne grane
direktne grane
poprečne grane
Prve tri grane povezuju dva čvora grafa, tako da
jedan je potomak drugog u DFS stablu.
Preciznije, grana
stabla povezuje oca sa sinom.
Povratna
grana povezuje potomka sa pretkom.
Direktna
grana povezuje pretka sa potomkom.
Poprečne
grane povezuju čvorove koji nisu srodnici u stablu i
prema dokazanoj lemi sa predavanja, one moraju biti usmerene zdesna
ulevo, te otud i naziv grana ulevo. Za DFS
Stablo neusmerenog grafa, pak vazi: grane povezanog
neusmerenog grafa ne mogu biti
poprečne grane za DFS stablo, tj. ne mogu povezivati
čvorove na različitim putevima od korena.
![]()
RESENJE:
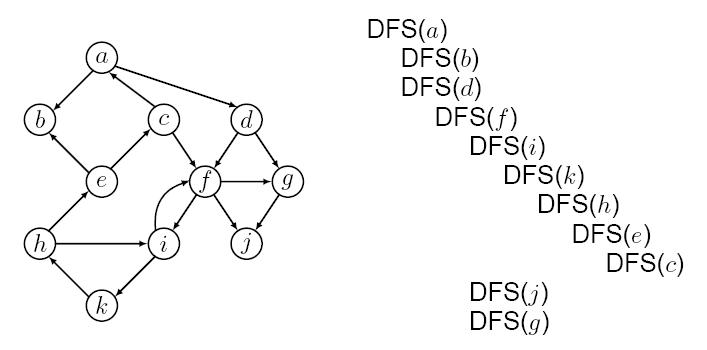
DFS stablo i numeracija
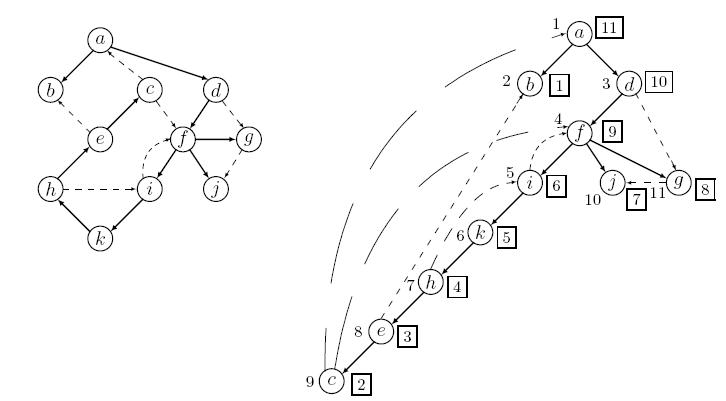

8.
Dat je usmeren graf G=(V,E), tako da V={A, B, C, D, E, F, G}, E={
(A,B), (A,D), (B,E), (B,F), (D,B), (E,D), (F,C), (F,E), (F,G), (G,C)
}.
Primeniti DFS obilazak i za svaki čvor iz V prikazati
početno vreme/završno vreme. Početno vreme
predstavlja vreme prvog nailaska na čvor u DFS algoirtmu.
Završno vreme se odnosi na vreme kada su obrađeni svi
susedi čvora. Redosled grana određen je
redosledom u spisku članova skupa E. Polazni čvor je čvor
A (gleda se leksikografski poredak).
REŠENJE:
Redosled obilaska čvorova grafa DFSom je: ABEDFCG, te je otuda numeracija a/b (gde a je redosled prvog nailaska na čvor, b je redosled napuštanja čvora)
A 1/?
B 2/?
C 6/?
D 4/?
E 3/?
F 5/?
G 7/?
9. Konstruisati algoritam linearne slozenosti koji u povezanom neusmerenom grafu G=(V,E) pronalazi čvor takav da i nakon izbacivanja tog čvora iz grafa, opet graf ostaje povezan.
REŠENJE:
Graf je povezan ako (u njegovom neusmerenom) obliku postoji put između ma koja dva čvora. Neusmereni oblik usmerenog grafa G=(V,E) jeste graf G bez orjentacije nad granama.
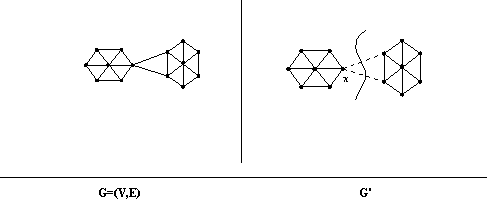
Kao rezultat primene algoritma DFS, gradi se specijalno povezujuće stablo, tzv. DFS stablo. Koren pretrage grafa u dubinu, tj. čvor v jeste koren DFS stabla.
Obilazeći graf G pretragom u dubinu (DFS) gradi se stablo i označavaju čvorovi.
Pri tome neki čvorovi će biti listovi DFS stabla.
Na početku se stavi da svaki v iz V jeste list, tj. v.indikator=1
Ako je čvor x iz V povezan sa bar jednim neoznačenim čvorom, onda je to dovoljno da odbacimo x kao list, tj. x.indikator=0 (jer se nalazi nivo iznad lista)
na kraju, ako se izbaci neki čvor koji jeste list DFS stabla, novi graf G' (dobijen iz G bez x) će ostati povezan
Algoritam Izbaciti(G,s)
ulaz: G , s (cvor neusmerenog i povezanog grafa G=(V,E) )
izlaz: za svaki v vazi da v.indikator=1 ako cvor v moze biti izbacen iz G
{
oznaciti s;
s.indikator=1;
for each (s,v)
if not oznacen(v)
{ Izbaciti(G,v);
v.indikator=0;
}
}Vremenska slozenost ovog algoritma (koji koristi DFS pretragu) odgovara vremenskoj složenosti DFS algoritma za povezane neusmerene grafove, pa zato jeste linearna po dimenziji ulaza, tj. svaka grana se pregleda do dva puta, te je slozenost proporcionalna broju grana, dok broj rekurzivnih pokretanja je |V|.
Da li izbacivanje čvora moze da se obavi za svaki povezan graf G? Zašto?
Naime, za svaki povezan graf postoji odgovarajuće DFS stablo. Svako stablo ima bar jedan list i to stablo ostaje povezano kada se list izbaci, te povezani neusmeren graf zaista sadrzi čvor koji se moze izbaciti, a da novi graf ostane povezan.
10. Dat je usmeren graf G=(V,E), tako da V={A, B, C, D, E, F, G, H}, E={ (A,B), (B,C), (B,G), (B,H), (C,F), (C,D), (D,C),(D,E), (F,G), (F,E), (G,F), (H,G), (H,A) }.
Odrediti: DFS stablo grafa, komponente povezanosti grafa.
11. Neka G=(V,E) je neusmeren graf. Skup grana F podskup od U naziva se skup povratnih grana ako svaki ciklus u G sadrži bar jednu granu iz F. Konstruisati algoritam za nalaženje minimalnog skupa povratnih grana.
REŠENJE:
Povezujuće stablo neusmerenog grafa G je njegov podgraf koji je stablo i sadrži sve čvorove iz G.
Kako svaki ciklus u G mora da sadrzi jednu granu iz skupa grana F => skup grana E\F ne sadrži niti jedan ciklus. Dakle, sto je manji skup F, to je veći skup E\F.
Maksimalni skup grana grafa bez ciklusa formira povezujuće stablo kod povezanih grafova (odnosno povezujuću sumu kod nepovezanog grafa). Dakle, minimalni skup F je komplement ma kog povezujućeg stabla grafa. (videti glavu 6.6 udžbenika).
12. Dat je usmereni graf G=(V,E) i njegov čvor v skupa V. Konstruisati algoritam složenosti O( |E| + |V| ) koji ispituje da li G jeste korensko stablo sa korenom v. Smatrati da su u korenskom stablu grane usmerene od korena ka listovima.
REŠENJE:
Korensko stablo jeste usmereno stablo koje poseduje posebno izdvojen čvor koji se zove koren, a sve grane su usmerene od korena.
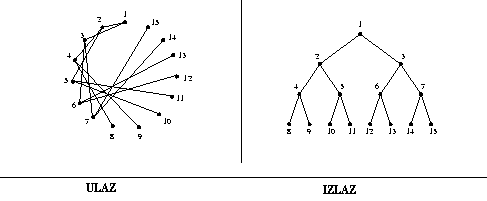
Kako ulazni stepen svakog čvora nije veći od jedan, usmeren graf je stablo akko je povezan i nema (usmerene) cikluse.
Na zadati usmeren graf G=(V,E) treba primeniti
algoritam za obilazak stabla smatrajuci pri tome da je cvor v njegov
koren i brojeci cvorove kroz koje se prolazi.
Ukoliko pri tom
obilasku broj čvorova kroz koje se prošlo bude veći od |V|,
graf G ima ciklus(e), te nije stablo;
ukoliko se obilazak završi
sa brojem čvorova kroz koje se proslo manjim od |V|, graf G nije
povezan, te nije stablo;
inače graf G jeste stablo.
Algoritam obilazak1(G,v})
ulaz: G=(V,E) (usmeren graf), v (cvor grafa G)
izlaz: broj ( brojac cvorova kroz koje se proslo)
{
markiraj v;
broj=broj+1 ;
ako je broj manji ili jednak od broja cvorova grafa G onda
za sve grane (v,w) do
if markiran(w) return -1;
else
obilazak1(G,w);
return broj;
}
Algoritam provera1(G,v)
ulaz: G=(V,E) (usmeren graf), v(cvor grafa G)
izlaz: odgovor na pitanje da li je graf G sa korenom v stablo
{
broj:=0 ;
obilazak1(G,v);
ako je broj manji od broja cvorova grafa G onda
write('graf G nije povezan');
ako je broj veci od broja cvorova grafa G onda write('graf G ima ciklus(e)')
inace write('graf G je stablo');
}
13. Neka je G = (V,E) usmereni graf i neka T je DFS stablo grafa G. G sadrzi usmereni ciklus ako i samo ako G sadrzi povratnu granu (u odnosu na T). Dokazati.
REŠENJE:
Prema DFS odlaznoj numeraciji (tj. v.Post je redni broj čvora v pri odlaznoj numeraciji čvorova grafa u DFS obilasku grafa tj. to je redni broj čvora u redosledu napustanja u izlaznoj obradi), za usmereno stablo važi:
Ako grana (u,v) jeste grana stabla ili direktna, onda: v.Post < u.Post (jer, v je potomak od u)
Ako grana (u,v) jeste poprečna, onda: v.Post < u.Post (jer, v je levo od u)
Ako grana (u,v) jeste povratna i v!=u, onda: v.Post > u.Post (jer, v je pravi predak od u)
Ako grana (u,v) jeste povratna i v==u (jer petlja jeste povratna grana), onda: v.Post = u.Post (jer, v je strogo predak od u) Dakle, za povratnu granu (u,v) v.Post >=u.Post
Lema1 (stavke 1-4): Grana (u, v) usmerenog grafa G je povratna ako i samo ako prema odlaznoj numeraciji (DFS) čvor u prethodi čvoru v, tj. u.Post <= v.Post
RESENJE ZADATKA:
<=
Ako je grana (u,v) povratna,
onda ona zajedno sa granama stabla na putu od u do v zatvara ciklus.
=>
Takođe je tačno
i suprotno tvrđenje: ako u grafu postoji ciklus, tada u njemu
mora da postoji povratna grana.
Zaista, pretpostavimo da u grafu
postoji ciklus koji čine grane (v1,
v2), (v2,v3), . . . (vk,
v1)
Ako k=1 (tj. ciklus je petlja), tada je grana (v,v)
povratna.
Ako je k veće od jedan, pretpostavimo da nijedna od
grana (v1, v2), (v2,v3),
. . . (vk-1, vk) nije povratna.
Po Lemi 1, onda važi
da v1.Post > v2.Post > . . . vk.Post,
odnosno vk.Post < v1.Post, pa je grana
(vk,v1) povratna.
Time je dokazano da u
svakom ciklusu postoji povratna grana.
14.
Napisati program kojim se ispituje da li je neorijentisani graf ciklican.RESENJE ZADATKA:
Provera se moze realizovati modifikovanjem algoritma DFS.
Ako na nekom koraku obilaza po dubini tekuci cvor i ima suseda koji je vec
posecen, a razlikuje se od "oca" cvora i (tj. cvora sa koga se doslo na cvor i), graf
sadrzi ciklus.
Algoritam se moze realizovati tako sto ce se funkciji DFS() dodati
parametar int otac - "otac" tekuceg cvora.
#include <iostream>
using namespace std;
const int maxN=20;
const int n=12; // cvorovi su numerisani od 0 do n
const char a[maxN][maxN]={... };
int mark[maxN];
int Cycl(int i, int otac)// Obilaz po dubini od zadatog cvora
{
mark[i]=1;
for (int k=0; k<=n; k++)
if (a[i][k] && (k!=otac))
if (mark[k]) return 1;
else if (Cycl(k,i)) return 1;
return 0;
}
int main()
{
bool Ok=false;
for (int i=0; i<=n; i++) mark[i]=0;
for (int i=0; i<=n; i++)
if (!mark[i] && Cycl(i,-1))
{cout << "Graf sadrzi ciklus!\n"; Ok=true; break; }
if (!Ok) cout << "Graf je drvo (ne sadrzi cikluse)!\n";
return 0;
}