Strukture podataka - grafovi (osnovni pojmovi)

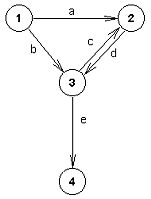
Graf G = ( V, E ) se sastoji od skupa čvorova V i skupa grana E, pri čemu grane predstavljaju relacije između čvorova.

Usmeren graf

Na slici je prikazan usmeren graf takav da V={1,2,3,4}, E={a,b,c,d}

Grane usmerenog grafa su uređeni parovi čvorova i redosled dva čvora koje povezuje grana je bitan.

Slika 1
 
 

Neusmeren graf

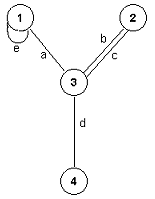
Grane neusmerenog grafa su neuređeni parovi čvorova.

Graf sa slike 2 je neusmeren i čvorovi 2 i 3 su povezani granama b i c.
 

Slika 2

  Specijalan primer grafa jeste stablo koje predstavlja povezan graf bez ciklusa, tj. svi čvorovi su povezani među sobom i nema cikličnih puteva kroz stablo. Ako je na stablu potrebno definisati hijerarhiju, onda se sve grane mogu usmeriti od "korena". Takva stabla se nazivaju korenska stabla. Koren je poseban izdvojen čvor stabla, a listovi stabla su čvorovi koji nemaju naslednike.

Stablo ili drvo je povezani graf koji (u svom neusmerenom obliku) ne sadrži cikluse.

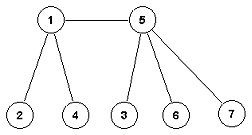
Stablo

Uobičajena su dva načina predstavljanja stabla:

    matricom povezanosti (susedstva)

    listom povezanosti (susedstva)

Matrica povezanosti grafa G je kvadratna matrica A reda n (gde |V|=n), gde A[i,j]=1 ako postoji grana od čvora v_i  do čvora v_j. Ostali elementu su nule.  Ako graf G je neusmeren, matrica je simetrična. Ako je broj grana u G mali, onda većina elemenata matrice će biti nula, ali će ona i dalje zauzimati prostor veličine n*n, sto je nedostatak ovog tipa reprezentacije ako se koristi za retke grafove.

Matrica povezanosti usmerenog grafa

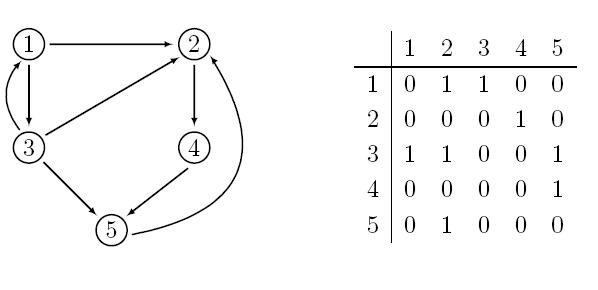
Matrica povezanosti usmerenog težinskog grafa

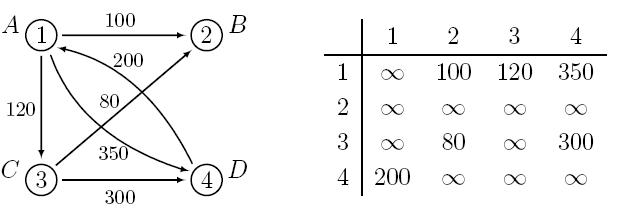
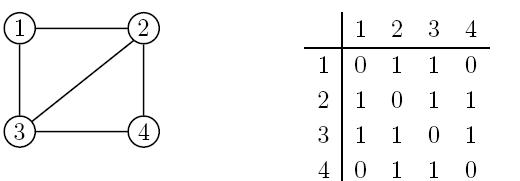
Matrica povezanosti neusmerenog grafa (Neusmerena grana {a, b} se predstavlja kao dve usmerene grane (a, b) i (b, a))

Lista povezanosti pak omogućuje da se ne vrši eksplicitno predstavljanje nepostojećih grana. Svakom čvoru pridružuje se povezana lista koja sadrži sve grane ka susednim čvorovima. Svaki element liste (tj. jednodimenzionog niza) sadrži indeks čvora grafa G i pokazivač na njegovu listu čvorova. Ako G je statički graf (tj. ne vrše se umetanja, brisanja), onda se za realizaciju liste povezanosti koristi niz dužine |V|+|E|, gde prvih |V| elemenata su pridruzeni cvorovima grafa, a vrednost na poziciji  j pridruzena cvoru  v_j sadrzi indeks pocetka spiska čvorova susednih čvoru  v_j.

Lista povezanosti