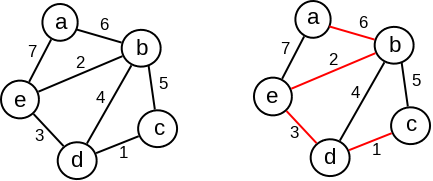
Razmotrimo sistem računara koje treba povezati optičkim kablovima tako da postoji veza između svaka dva računara. Poznati su troškovi postavljanja kabla između svaka dva računara. Cilj je projektovati mrežu optičkih kablova tako da ukupna cena mreže bude minimalna. Sistem računara može biti predstavljen neusmerenim grafom čiji čvorovi odgovaraju računarima, a grane – potencijalnim vezama između računara, sa odgovarajućim (pozitivnim) cenama. Tada se problem svodi na pronalaženje povezanog podgrafa (sa granama koje odgovaraju postavljenim optičkim kablovima) koji sadrži sve čvorove, takav da mu ukupna suma težina grana bude minimalna (slika 1). Nije teško videti da taj podgraf mora da bude drvo. Naime, ako bi podgraf imao ciklus, onda bi se iz ciklusa mogla ukloniti proizvoljna grana, čime bi se dobio podgraf koji je i dalje povezan, a ima manju ukupnu težinu. Traženi podgraf zove se minimalno povezujuće (razapinjuće) drvo (MCST, skraćenica od engl. minimum–cost spanning tree) i ima mnogo primena. Sličan prethodnom problemu je i problem povezivanja \(N\) gradova autoputevima, tako da postoji put između svaka dva grada, a da ukupna cena izgradnje autoputa bude minimalna moguća. Minimalno povezujuće drvo ima primenu i u konstrukciji približnih algoritama, na primer, za rešavanje problema trgovačkog putnika.

Dakle, problem kojim se bavimo je konstrukcija efikasnog algoritma za nalaženje minimalnog povezujućeg drveta u datom neusmerenom težinskom grafu.
Problem. Za zadati neusmereni povezani težinski graf \(G=(V,E)\) konstruisati neko povezujuće drvo \(T\) minimalne težine.
Ako su sve grane grafa međusobno različite težine, minimalno povezujuće drvo je jedinstveno određeno (što ne mora biti slučaj kada postoje grane iste težine).
Postoji više različitih algoritama za određivanje minimalnog povezujućeg drveta datog grafa: mi ćemo razmotriti dva – Primov i Kraskelov algoritam.
Prilikom konstrukcije grafovskih algoritama prirodno je pokušati indukcijom po broju čvorova ili po broju grana. Na primer, pronalaženje najkraćih puteva iz jednog čvora u acikličnom grafu kao i Dajkstrin algoritam se mogu opisati tako što se iz grafa izbaci jedan čvor (poslednji u odgovarajućem poretku), rekurzivno reši smanjeni problem i na kraju doda izbačeni čvor. Naravno, implementacija teče iterativno dodajući jedan po jedan čvor, pri čemu se čvorovi moraju obrađivati u odgovarajućem redosledu.
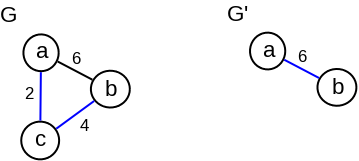
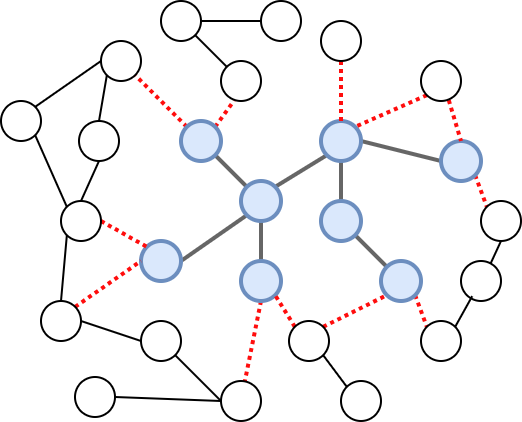
Nažalost, takav pristup se ne može jednostavno prilagoditi rešavanju problema minimalnog povezujućeg drveta. Naime, u opštem slučaju ne postoji neki prirodan redosled u kom bi se čvorovi obrađivali. Izbačeni čvor može biti artikulaciona tačka i razbiti graf na nepovezane komponente tako da se ne dobije problem istog oblika. Možemo odrediti minimalnu povezujuću šumu za posebne komponente, ali to komplikuje algoritam. Čak i kada se izbacivanjem čvora dobije povezan graf, nije jasno kako bi ubacivanje novog čvora uticalo na pronađeno minimalno povezujuće drvo manjeg grafa. Naime, nemamo garanciju da je minimalno povezujuće drvo podgrafa poddrvo minimalnog povezujućeg drveta celog grafa (slika 2). Da bi ubačeni čvor bio povezan sa ostalima, sigurno je potrebno da neka grana koja ga spaja sa susedima bude uključena u krajnje drvo. Međutim, moguće je da umesto samo jedne takve grane u drvo treba ubaciti i više njih, a izbaciti neke grane ranije konstruisanog poddrveta. Analiza ovog pristupa postaje komplikovana i odustaćemo od nje, jer, kao što ćemo videti postoje jednostavniji, veoma efikasni algoritmi.
Do sličnog zaključka se dolazi i ako se pokuša indukcija po broju grana. Za razliku od čvorova među kojima ne možemo unapred uspostaviti neki prirodan redosled, grane se prirodno mogu urediti po težini i možemo uticati na to koju granu ćemo izbaciti, rekurzivno rešiti potproblem i na kraju je ponovo vratiti u drvo. Važi (što ćemo kasnije i formalno dokazati) da najkraća grana grafa mora biti uključena u minimalno povezujuće drvo. Zato je prirodno nju ukloniti iz grafa, rešiti rekurzivno potproblem (primeniti induktivnu hipotezu) i na kraju je uključiti. Da li je ovo regularna primena indukcije?
Prvi problem u ovakvoj primeni indukcije je u tome što posle uklanjanja grane, dobijeni problem nije ekvivalentan polaznom. Naime, izbor jedne grane ograničava mogućnosti izbora drugih grana.
Primer 2.10.1. 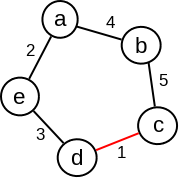
Razmotrimo primer grafa sa slike ??. Grana \((c,d)\) je grana minimalne težine u grafu, i ako nju uklonimo i problem svedemo na traženje minimalnog povezujućeg drveta u grafu \(G\) bez grane \((c,d)\), dobijamo da njega čine sve ostale grane grafa: grane \((d,e), (e,a), (a,b)\) i \((b,c)\). Dodavanjem grane \((c,d)\) u ovo minimalno povezujuće drvo dobijamo ciklus, a znamo da ciklus ne može biti deo minimalnog povezujućeg drveta.
Drugi problem sa primenom ovakve induktivne hipoteze je taj što uklonjena grana može biti most i nakon njenog uklanjanja graf ne mora da ostane povezan.
Primer 2.10.2. Razmotrimo graf sa slike 3: nakon uklanjanja grane \((c,d)\) minimalne težine, graf se raspada na dve komponente povezanosti.
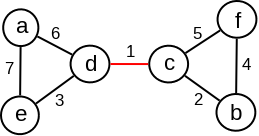
Možemo rekurzivno konstruisati minimalnu povezujuću šumu, ali ponovo, kao i u slučaju indukcije po broju čvorova, odustajemo od ovog pristupa, jer postoje jednostavniji.
Jedan mogući pristup rešavanju ovog problema je da se tokom izvršavanja algoritma minimalno povezujuće postupno gradi, dodajući u svakom koraku trenutnom poddrvetu jednu novu granu i jedan novi čvor. Prema tome, indukcija se ovde ne izvodi po veličini grafa (broju grana ili čvorova grafa), već prema broju grana u poddrvetu minimalnog povezujućeg drveta koje se gradi.
Induktivna hipoteza. Za zadati povezan graf \(G=(V,E)\) umemo da pronađemo drvo \(T_k\) sa \(k\) grana (\(k < |V| - 1\)), tako da je drvo \(T_k\) poddrvo nekog minimalnog povezujućeg drveta \(T\) grafa \(G\).
Bazni slučaj je \(k=0\). Pošto svaki čvor grafa pripada njegovom minimalnom povezujućem drvetu \(T\) (koje postoji, jer je graf povezan), drvo \(T_0\) može da sadrži proizvoljni čvor grafa i nijednu granu.
Pretpostavimo da smo pronašli drvo \(T_k\) koje zadovoljava induktivnu hipotezu i da je potrebno da \(T_k\) proširimo narednom granom. Kako da pronađemo novu granu za koju ćemo biti sigurni da pripada nekom minimalnom povezujućem drvetu? U svakom povezujućem drvetu koje proširuje drvo \(T_k\) mora da postoji bar jedna grana koja povezuje neki čvor iz \(T_k\) sa nekim čvorom u ostatku grafa. Neka je \(E_k\) skup svih takvih grana. Pošto je graf povezan, taj skup mora biti neprazan. Za narednu granu uzimamo proizvoljnu granu sa najmanjom težinom iz \(E_k\). Tvrdimo da svaka takva grana pripada nekom minimalnom povezujućem drvetu \(T\).
Lema 2.10.1. Neka je \(T_k\) poddrvo nekog minimalnog povezujućeg drveta \(T\) težinskog grafa \(G = (V, E)\) i neka je \(E_k\) skup grana koje povezuju čvorove iz \(T_k\) sa čvorovima van \(T_k\). Neka je \(e = (u, v)\) neka od grana najmanje težine među granama iz \(E_k\). Tada postoji minimalno povezujuće drvo \(T'\) grafa \(G\) koje sadrži sve grane iz \(T_k\) i granu \(e\).
Dokaz. Ako drvo \(T\) sadrži granu \(e\), onda je ono traženo drvo \(T'=T\).
Ako \(T\) ne sadrži \(e\), ono sadrži tačno jedan put od \(u\) do \(v\). Pošto grana \((u, v)\) ne pripada minimalnom povezujućem drvetu \(T\), onda ona ne pripada ni putu od \(u\) do \(v\) kroz grane drveta \(T\). Međutim, pošto \(u\) pripada, a \(v\) ne pripada drvetu \(T_k\), na tom putu mora da postoji bar još jedna grana \((u',v')\) takva da \(u'\in T_k\) i \(v'\notin T_k\). Razmotrimo odnos težina grana \((u,v)\) i \((u',v')\):
Algoritam se, dakle, sprovodi na sledeći način. Drvo \(T\) se inicijalizuje drvetom \(T_0\) koje sadrži samo jedan (proizvoljno odabrani) čvor. U svakoj iteraciji se vrši proširivanje trenutno konstruisanog drveta \(T_k\) jednom granom i čvorom, tako što se pronalazi neka grana iz skupa \(E_k\) koji sadrži sve grane koje povezuju \(T_k\) sa nekim čvorom van \(T_k\), a koja ima najmanju težinu od svih grana u tom skupu (ako ima više takvih, bira se proizvoljna).
Umesto čuvanja i ažuriranja celog skupa \(E_k\), za svaki čvor \(v\) van \(T_k\) možemo u nizu pamtiti rastojanje od drveta \(T_k\), tj. minimalnu težinu grane od \(v\) do nekog čvora iz \(T_k\) (ako takva grana ne postoji, vrednost postavljamo na \(+\infty\)) i u svakom koraku možemo određivati minimum tog niza. Kada se odabere grana najmanje težine iz \(E_k\) i njen čvor \(v \notin T_k\), analiziramo sve grane koje vode od \(v\) do nekog čvora \(w\) van \(T_k\) i ako je težina neke takve grane \((v, w)\) manja od trenutnog rastojanja \(w\) od drveta \(T_k\), ažuriramo to rastojanje (i granu koja od drveta vodi do njega).
Radi efikasnog nalaženja minimuma, sve grane skupa \(E_k\) možemo čuvati u redu sa prioritetom, uređenom po dužinama grana. Nakon dodavanja novog čvora \(v\) u \(T_k\), u red se dodaju grane koje ga spajaju sa čvorovima van \(T_k\). Međutim, neke grane koje su bile u \(E_k\) ne treba više da budu, jer sada spajaju dva čvora u drvetu. Slično kao kod Dajkstrinog algoritma i ovde možemo koristiti lenjo ažuriranje reda sa prioritetom i te grane ne moramo brisati iz reda. Zato, kada se grana minimalne težine izvadi iz reda sa prioretom, treba proveriti da li ona spaja čvor u \(T_k\) sa čvorom van njega. Ako spaja dva čvora unutar \(T_k\), treba je prosto preskočiti.
Postupak se završava kada se konstruiše drvo \(T_{|V|-1} \equiv T\), jer ono sadrži sve čvorove grafa (pošto je broj čvorova uvek za jedan veći od broja grana, tada drvo povezuje svih \(|V|\) čvorova). Pošto je na osnovu leme 2.10.1 i ono poddrvo nekog minimalnog povezujućeg drveta, ono mora biti minimalno povezujuće drvo.
Opisani algoritam poznat je pod nazivom Primov algoritam i sličan je Dajkstrinom algoritmu za nalaženje najkraćih puteva od zadatog čvora. Interesantno je da je ovaj algoritam prvi osmislio Vojteh Jarnik 1930. godine, a da su tek kasnije nezavisno do njega došli Robert Prim 1957. godine i Edzger Dajkstra 1959. godine.
Iz opisa induktivne konstrukcije i leme 2.10.1 sledi sledeća teorema.
Teorema 2.10.1. [Korektnost Primovog algoritma] Za proizvoljan neusmeren povezan težinski graf \(G=(V, E)\) Primov algoritam konstruiše jedno minimalno povezujuće drvo.
Jedina razlika između Primovog i Dajkstrinog algoritma je u tome što se ne traži čvor van trenutnog skupa koji ima minimalno rastojanje od početnog čvora, već se traži čvor van trenutnog skupa koji ima minimalno rastojanje od trenutno konstruisanog drveta. Ostatak algoritma prenosi se praktično bez promene.
Naredni aplet prikazuje rad Primovog algoritma.
U narednom apletu možete proveriti svoje razumevanje rada Primovog algoritma.
// Primov algoritam za odredjivanje minimalnog povezujuceg drveta
void minimalnoPovezujuceDrvoPrim() {
int brojCvorova = listaSuseda.size();
// da li je cvor ukljucen u trenutno drvo
vector<bool> uDrvetu(brojCvorova, false);
// najkrace rastojanje od cvora do trenutnog drveta tj.
// duzina najkrace grane koja povezuje trenutno drvo i cvor
vector<Tezina> minRastojanja(brojCvorova, INF);
// roditeljski cvor svakog cvora u minimalnom povezujucem drvetu
vector<Cvor> roditelji(brojCvorova, -1);
// uredjen par koji čine rastojanje do cvora i broj cvora;
// redosled elemenata mora biti ovakav zbog operacije poredjenja parova
typedef pair<Tezina, Cvor> RastojanjeCvora;
// min-hip u koji smestamo duzine najkracih grana od drveta do svih cvorova
priority_queue<RastojanjeCvora,
vector<RastojanjeCvora>,
greater<RastojanjeCvora>> rastojanja;
// pocetni cvor moze biti bilo koji
Cvor start = 0;
// ubacujemo pocetni cvor u hip i postavljamo duzinu grane do njega na 0
rastojanja.emplace(0, start);
minRastojanja[start] = 0;
// broj cvorova trenutno ukljucenih u minimalno povezujuce drvo
int brojCvorovaUDrvetu = 0;
// dok se svi cvorovi ne ukljuce u drvo
while (brojCvorovaUDrvetu < brojCvorova) {
// izdvajamo cvor cvor najblizi drvetu (u prvom koraku izdvajamo pocetni cvor)
auto [rastojanje, cvor] = rastojanja.top();
rastojanja.pop();
// ako je taj cvor vec u drvetu, treba ga preskociti
// ovo se moze desiti jer vrsimo lenjo azuriranje hipa
if (uDrvetu[cvor])
continue;
// dodajemo cvor u drvo
uDrvetu[cvor] = true;
brojCvorovaUDrvetu++;
// za sve susede tekuceg cvora
for (const auto& [sused, tezina] : listaSuseda[cvor]) {
if (!uDrvetu[sused]) {
// ako je grana iz tekuceg cvora do sused kraca od
// prethodno najkrace grane iz drveta do tog suseda,
// azuriramo vrednost najkrace grane i roditeljskog cvora
if (tezina < minRastojanja[sused]) {
minRastojanja[sused] = tezina;
roditelji[sused] = cvor;
// ubacujemo element u hip;
// ako je postojala prethodna vrednost, ne brisemo je:
// nova vrednost ce se naci u hipu iznad stare
rastojanja.emplace(minRastojanja[sused], sused);
}
}
}
}
cout << "Minimalno povezujuce drvo se sastoji od grana: " << endl;
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
if (roditelji[cvor] != -1)
cout << "(" << roditelj[cvor] << "," << cvor << ") težine "
<< minRastojanja[cvor] << endl;
}Kada se koristi red sa prioritetom, složenost Primovog algoritma identična je složenosti Dajkstrinog algoritma za nalaženje najkraćih rastojanja od zadatog čvora i iznosi \(O((|E|+|V|)\log |V|)\).
Ukoliko su težine svih grana u grafu međusobno različite, minimalno povezujuće drvo grafa biće jedinstveno.
Primer 2.10.3. Primov algoritam za konstrukciju minimalnog povezujućeg drveta ilustrovaćemo primerom na slici 5. Čvor u prvoj koloni tabele je onaj koji je dodat u odgovarajućem koraku. Prvi dodati čvor je \(v\), i u prvoj vrsti navedeni su čvorovi do kojih postoje grane iz čvora \(v\) sa svojim težinama. U svakoj vrsti bira se grana sa najmanjom težinom. Spisak trenutno najboljih grana i njihovih težina ažurira se u svakom koraku (prikazani su samo krajevi grana). Na slici grafa su grane koje pripadaju minimalnom povezujućem drvetu podebljane.

Primov algoritam je primer pohlepnog algoritma, jer se u svakom koraku bira grana skupa \(E_k\) sa najmanjom težinom, tj. izbor lokalnog minimuma vodi i ka globalnom minimumu.
Intuitivno je jasno da je poželjno da minimalno povezujuće drvo sadrži grane grafa sa što manjim težinama. Ako su sve težine grafa međusobno različite, grana najmanje težine u grafu mora biti uključena u minimalno povezujuće drvo. Ako ona ne bi bila uključena, onda bi njeno dodavanje minimalnom povezujućem drvetu zatvorilo neki ciklus; uklanjanjem proizvoljne druge grane iz tog ciklusa ponovo se dobija drvo, ali manje težine — što je u suprotnosti sa pretpostavkom o minimalnosti konstruisanog povezujućeg drveta. Ovo inspiriše algoritam koji obilazi grane grafa u neopadajućem redosledu težina i uključuje jednu po jednu u graf. Ako postoji više grana iste najmanje težine koje mogu biti dodane, bira se bilo koja od njih. Ipak, potrebno je voditi računa da neke grane sa ranije dodatim granama zatvaraju ciklus i njih moramo preskočiti.
Dakle, i drugi efikasan algoritam za određivanje minimalnog povezujućeg drveta datog neusmerenog težinskog grafa \(G=(V,E)\) je pohlepan, jer u svakom koraku bira jednu od najkraćih raspoloživih grana, ali do minimalnog povezujućeg drveta ne dolazi dodavanjem novih grana na trenutno drvo, nego na trenutnu šumu.
Indukcija u ovom algoritmu teče po broju obrađenih grana u neopadajućem redosledu težine grana.
Induktivna hipoteza. Za zadati povezan graf \(G = (V, E)\) i skup njegovih \(k\) grana \(E_k \subseteq E\) najmanje težine umemo da odredimo šumu \(K\), koja je deo nekog minimalnog povezujućeg drveta grafa \(G\). To drvo sadrži sve grane skupa \(K\), a ne sadrži ni jednu granu skupa \(L = E_k \setminus K\).
Inicijalno svaki čvor grafa predstavlja zasebno drvo i odgovarajuća šuma sadrži \(|V|\) drveta i nijednu granu. Zatim se postepeno spajaju po dva drveta ove šume, dodavanjem grana. Dodavanjem svake nove grane, broj drveta u šumi se smanjuje za \(1\), te će se nakon dodavanja \(|V|-1\) grane dobiti tačno jedno drvo. Pri tome se grane koje se dodaju razmatraju u neopadajućem redosledu težina; ako grana koja je sledeća na redu povezuje dva čvora u različitim drvetima trenutne šume, onda se ta grana uključuje u šumu, čime se ta dva drveta spajaju u jedno. U protivnom, ako grana povezuje dva čvora iz istog drveta trenutne šume, grana se preskače.
Ovaj algoritam je prvi objavio Džozef Kraskel 1956. godine i poznat je pod nazivom Kraskelov algoritam.
Dokažimo da će ovaj algoritam uvek vratiti neko minimalno povezujuće drvo datog grafa.
Teorema 2.10.2. [Korektnost Kraskelovog algoritma] Za proizvoljan neusmeren povezan težinski graf \(G = (V, E)\), Kraskelov algoritam konstruiše jedno minimalno povezujuće drvo.
Dokaz. Lako se pokazuje da algoritam vraća povezujuće drvo datog grafa (jer na kraju imamo \(n\) čvorova povezanih sa \(n-1\) grana, bez ciklusa, što mora biti drvo). Treba pokazati da je ono i minimalno.
Dokazaćemo indukcijom da u svakom koraku algoritma (prilikom razmatranja bilo koje grane) postoji minimalno povezujuće drvo \(T\) grafa koje sadrži sve grane skupa \(K\) koje su odabrane u prethodnim koracima i ne sadrži ni jednu granu skupa \(L\) koje su odbačene u prethodnim koracima. Nakon obrade svih grana, \(K\) je drvo koje mora biti jednako minimalnom povezujućem drvetu koje ga sadrži.
U početnom koraku nije niti prihvaćena, niti odbačena ni jedna grana grafa. Pošto je graf povezan on ima minimalno povezujuće drvo \(T\). To drvo zadovoljava uslov jer obuhvata početni prazan skup grana \(K = \emptyset\) i ne obuhvata ni jednu granu skupa \(L = \emptyset\).
Neka je \(e\) naredna grana koju razmatra Kraskelov algoritam u trenutku kada su u šumu prethodno dodate grane skupa \(K\) i odbačene grane iz nekog skupa \(L\). Ona može biti dodata u tekuću šumu ili odbačena.
Razmotrimo slučaj dodavanja nove grane \(e\) u šumu. Neka je \(T\) neko minimalno povezujuće drvo koje obuhvata sve grane skupa \(K\) i nijednu granu iz \(L\) (ono postoji na osnovu induktivne hipoteze). Nova šuma \(K' = K \cup \{e\}\) sadrži i granu \(e\) i ona ne zatvara ciklus sa ostalim granama iz \(K\).
Ako grana \(e\) pripada drvetu \(T\), tada je \(T'=T\) traženo minimalno povezujuće drvo koje sadrži sve grane iz skupa \(K' = K \cup \{e\}\) i nijednu granu iz skupa \(L'=L\).
Ako grana \(e\) ne pripada drvetu \(T\), onda se njenim dodavanjem u \(T\) zatvara neki ciklus u drvetu \(T\) (jer u drvetu \(T\) postoji neki drugi put koji povezuje krajnje čvorove grane \(e\)). Taj ciklus ne postoji u šumi \(K \cup {e}\) (jer se u suprotnom grana \(e\) ne bi dodavala šumi). Zato u tom ciklusu mora da postoji neka grana \(e'\), različita od \(e\), koja pripada drvetu \(T\), ali ne pripada šumi \(K\). Pošto \(e'\) pripada drvetu \(T\), ona ne može da pripada skupu \(L\) odbačenih grana (jer \(T\) ne sadrži ni jednu odbačenu granu iz skupa \(L\)). Dakle, \(e'\) ne pripada ni skupu \(L\) ni skupu \(K\) i različita je od \(e\). Zato je Kraskelov algoritam još nije razmatrao, pa njena težina mora biti veća ili jednaka od težine grane \(e\). Izbacivanjem grane \(e'\) iz drveta \(T\) i dodavanjem grane \(e\) dobijamo novo drvo \(T'\) (ono ima isti broj čvorova i grana kao drvo \(T\), a ostaje povezano, jer se jedna grana koja zatvara ciklus menja drugom granom tog ciklusa). Ukupna težina drveta \(T'\) ne može biti manja od težine drveta \(T\), jer je \(T\) minimalno povezujuće drvo, ne može biti veća, jer težina grane \(e\) koja se dodaje nije veća od težine grane \(e'\) koja se izbacuje, pa ukupne težine drveta \(T\) i \(T'\) moraju biti jednake. \(T'\) je zato takođe minimalno povezujuće drvo, a ono sadrži sve grane iz skupa \(K' = K\cup \{e\}\) i ne sadrži ni jednu granu iz skupa odbačenih grana \(L'=L\).
Razmotrimo na kraju slučaj odbacivanja grane \(e\). Jedini razlog da se ona odbaci je kada ona zatvara neki ciklus sa granama iz \(K\). Međutim, pošto se sve grane iz \(K\) nalaze u drvetu \(T\), a u \(T\) nema ciklusa, grana \(e\) ne pripada drvetu \(T\). Zato je \(T\) traženo minimalno povezujuće drvo koje sadrži sve grane iz skupa \(K' = K\) i ni jednu granu iz skupa \(L' = L \cup \{e\}\). \(\Box\)
Za utvrđivanje da li su krajnji čvorovi \(u\) i \(v\) tekuće grane \((u,v)\) u istom ili u različitim drvetima trenutne šume, može se iskoristiti struktura podataka za disjunktne skupove (union-find): trenutna drveta šume su disjunktni podskupovi skupa čvorova grafa. Operacije pronadji(u) i pronadji(v) pronalaze predstavnike \(u',v'\) dva podskupa (korene drveta kojim su oni predstavljeni), pa su čvorovi \(u\) i \(v\) u istom podskupu ako i samo ako je \(u'=v'\). Ako je \(u'\neq v'\), onda se ta dva podskupa zamenjuju svojom unijom, tj. primenjuje se operacija unija(u',v'), a dva poddrveta trenutne šume se granom spajaju u jedno.
// funkcija za inicijalizaciju union-find strukture
void UF_inicijalizuj(vector<int>& UF_roditelj, vector<int>& UF_rang, int n) {
// svaki cvor je podskup za sebe
for (int i = 0; i < n; i++) {
UF_roditelj[i] = i;
UF_rang[i] = 0;
}
}
// funkcija koja izracunava kom podskupu pripada neki element
int UF_pronadji(int x, vector<int>& UF_roditelj) {
int koren = x;
while (koren != UF_roditelj[koren])
koren = UF_roditelj[koren];
while (x != koren) {
int tmp = UF_roditelj[x];
UF_roditelj[x] = koren;
x = tmp;
}
return koren;
}
// funkcija koja pravi uniju dva podskupa
void UF_unija(int x, int y, vector<int>& UF_roditelj, vector<int>& UF_rang) {
int fx = UF_pronadji(x, UF_roditelj);
int fy = UF_pronadji(y, UF_roditelj);
if (UF_rang[fx] < UF_rang[fy])
UF_roditelj[fx] = fy;
else if (UF_rang[fy] < UF_rang[fx])
UF_roditelj[fy] = fx;
else {
UF_roditelj[fx] = fy;
UF_rang[fy]++;
}
}
// Kraskelov algoritam za odredjivanje minimalnog povezujuceg drveta
void minimalnoPovezujuceDrvoKraskel() {
int brojCvorova = listaSuseda.size();
// roditelj cvora u union-find strukturi
vector<Cvor> UF_roditelj(brojCvorova);
// rang cvora u union-find strukturi
vector<int> UF_rang(brojCvorova);
// inicijalizujemo union-find strukturu
// svaki cvor grafa predstavlja podskup za sebe
UF_inicijalizuj(UF_roditelj, UF_rang, brojCvorova);
// kreiramo jedinstveni niz svih grana u grafu
typedef pair<Cvor, Cvor> Grana;
vector<pair<Tezina, Grana>> grane;
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
for (const auto& [sused, tezina]: listaSuseda[cvor]) {
Grana grana{cvor, sused};
grane.emplace_back(tezina, grana);
}
// sortiramo skup grana u neopadajucem redosledu težina
sort(grane.begin(), grane.end());
// grane koje pripadaju konacnom minimalnom povezujucem drvetu
vector<pair<Grana, Tezina>> drvo;
// drvo ce sadrzati |V| - 1 grana, pa unapred rezervisemo memoriju
drvo.reserve(brojCvorova - 1);
// prolazimo redom kroz skup grana
for (const auto& [tezina, grana] : grane) {
// krajnji cvorovi grane
auto [u, v] = grana;
// predstavnici cvorova u union-find strukturi
Cvor predstavnik_u = UF_pronadji(u, UF_roditelj);
Cvor predstavnik_v = UF_pronadji(v, UF_roditelj);
// ako tekuca grana povezuje dva cvora koja pripadaju
// razlicitim drvetima onda tu granu dodajemo u minimalno povezujuce drvo
// i pravimo uniju skupova cvorova koji pripadaju tim drvetima
if (predstavnik_u != predstavnik_v) {
// spajamo drveta kojima pripadaju u i v (dodavanjem grane uv)
UF_unija(predstavnik_u, predstavnik_v, UF_roditelj, UF_rang);
// granu dodajemo u skup grana koje cine sumu (tj. drvo na kraju)
drvo.emplace_back(grana, tezina);
// drvo je kompletno konstruisano kada je broj grana za jedan manji
// od broja cvorova
if (drvo.size() == brojCvorova - 1)
break;
}
}
cout << "Minimalno povezujuce drvo se sastoji od grana: " << endl;
for (const auto& [grana, tezina] : drvo) {
auto [u, v] = grana;
cout << "(" << u << "," << v << ") težine "
<< tezina << endl;
}
}Funkcija za inicijalizaciju union-find strukture za disjunktne skupove je složenosti \(O(|V|)\), dodavanje grana u skup grana je složenosti \(O(|E|)\), njihovo sortiranje je složenosti \(O(|E|\log|E|)\), a nakon toga se glavna petlja izvršava \(|E|\) puta, dok su operacije koje se izvršavaju u petlji (UF_pronadji i UF_unija) složenosti \(O(\log|V|)\). Dakle, ukupna složenost Kraskelovog algoritma iznosi \(O(|V|)+O(|E|)+O(|E|\log|E|)+O(|E|\log|V|)= O(|E|\log |V|)\) (koristimo činjenicu da je \(O(\log|E|)=O(\log |V|)\) zbog \(|E|\le |V|^2\)).
Primer 2.10.4. Primer izvršavanja Kraskelovog algoritma za graf sa slike 5 prikazan je u tabeli 1. Prolazimo redom kroz skup grana prema neopadajućem redosledu težina i završavamo obradu kada u skup dodamo \(|V|-1\) (u ovom slučaju \(8\)) grana. Kao rezultat dobijamo minimalno povezujuće drvo prikazano na slici 5.
| naredna grana | dužina grane | uključena u MCST? | trenutna šuma |
|---|---|---|---|
| \((a,v)\) | \(1\) | da | \(\underline{v},\underline{a},b,c,d,e,f,g,h\) |
| \((a,c)\) | \(2\) | da | \(\underline{a}v,b,\underline{c},d,e,f,g,h\) |
| \((b,e)\) | \(3\) | da | \(acv,\underline{b},c,d,\underline{e},f,g,h\) |
| \((c,d)\) | \(4\) | da | \(a\underline{c}v,be,\underline{d},e,f,g,h\) |
| \((e,h)\) | \(5\) | da | \(acdv, b\underline{e},f,g,\underline{h}\) |
| \((b,v)\) | \(6\) | da | \(acd\underline{v},\underline{b}eh,f,g\) |
| \((d,e)\) | \(7\) | ne | \(abc\underline{de}hv,f,g\) |
| \((d,v)\) | \(8\) | ne | \(abc\underline{d}eh\underline{v},f,g\) |
| \((c,f)\) | \(9\) | da | \(ab\underline{c}dehv,\underline{f},g\) |
| \((g,h)\) | \(10\) | da | \(abcdef\underline{h}v,\underline{g}\) |
| \(abcdefghv\) |
Naredni aplet prikazuje rad Kraskelovog algoritma.
U narednom apletu možete proveriti svoje razumevanje rada Kraskelovog algoritma.
Konačno, napomenimo da se na sličan način može konstruisati i povezujuće drvo sa maksimalnom mogućom ukupnom težinom grana, tzv. maksimalno povezujuće drvo grafa. Jedino je potrebno grane obrađivati u obrnutom redosledu.
Zadaci: