Postoji mnogo situacija u kojima se javlja potreba da se izračunaju najkraći putevi kroz graf. Na primer, graf može odgovarati auto–karti: čvorovi su gradovi, a dužine grana dužine direktnih puteva između gradova (ili vreme potrebno da se taj put pređe, ili troškovi da se izgradi). Zadatak je pronaći najkraći put (u smislu dužine, proteklog vremena ili potrebnog ulaganja) od jednog grada do drugog. Zadaci ovog tipa se formulišu na proizvoljnim težinskim grafovima, tako što se pod dužinom puta podrazumeva zbir svih težina grana na tom putu (pa je najkraći put zapravo put sa najmanjim zbirom težina grana).
Algoritmi za određivanje najkraćih puteva igraju važnu ulogu i u rutiranju podataka kroz komunikacionu mrežu, u kontekstu određivanja najefikasnijih putanja (u smislu minimizovanja kašnjenja ili zagušenja) od izvora do odredišta. Algoritmi za računanje najkraćih puteva nalaze primenu i u optimizovanju lanca snabdevanja, odnosno u određivanju najkraćih puteva za transport robe od proizvođača do distributivnih centara, a zatim i krajnjih potrošača.
Iako je često potrebno da se nađe najkraći put od konkretnog početnog do konkretnog završnog čvora, nalaženje tog najkraćeg puta nije moguće bez nalaženja najkraćih puteva od početnog do mnogih drugih čvorova grafa. Zato se obično razmatra sledeći problem.
Problem. Za dati usmereni težinski graf \(G=(V,E)\) i jedan njegov čvor \(s\) pronaći najkraće puteve (puteve sa najmanjim zbirom težina grana) od čvora \(v\) do svih ostalih čvorova u grafu \(G\).
Primer 2.9.1. Razmotrimo primer određivanja najkraćih puteva od čvora \(1\) do svih ostalih čvorova u grafu sa slike ??:
najkraći put do čvora \(3\) je direktna grana \((1,3)\) dužine \(1\),
najkraći put do čvora \(2\) je put \((1,3,2)\) ukupne dužine \(1+2=3\), a ne direktna grana \((1,2)\) dužine \(5\),
najkraći put do čvora \(0\) je put \((1,3,2,0)\) ukupne dužine \(1+2+1=4\).
U narednom apletu možete pokušati da samostalno odredite najkraće puteve od jednog do ostalih čvorova u neusmerenom grafu.
Pretpostavimo najpre da je graf \(G=(V,E)\) aciklički. U tom slučaju problem je lakši i njegovo rešenje pomoći će nam da problem rešimo i u opštem slučaju. Težine grana mogu biti proizvoljne (pozitivne, nula, pa čak i negativne).
Na primer, ako je graf drvo i tražimo najkraće puteve od korena do svih ostalih čvorova, tada do svakog čvora postoji jedinstven put i on je ujedno i najkraći. Dužine tih puteva se mogu odrediti bilo rekurzivno (tako što se za svaki čvor rekurzivno odredi najkraći put od korena do njegovog roditelja, koji se zatim produžava granom od roditelja do čvora), bilo iterativno (tako što će se najkraći put od svakog čvora produžiti granama do njegovih naslednika). Primetimo da se u osnovi zapravo krije algoritam zasnovan na dinamičkom programiranju (koji je u slučaju rekurzivne implementacije odozgo-naniže, a u slučaju iterativne odozdo-naviše), o čemu će više reči biti u nastavku.
I za acikličke grafove koji nisu drveta do rešenja se može doći na sličan način.
Opišimo rekurzivno rešenje problema (ne obazirući se u početku na efikasnost). Neka je \(|V|=n\). Pošto je graf aciklički, možemo da iskoristimo topološko sortiranje grafa i da čvorove u topološkom redosledu označimo sa \(v_1, v_2, \ldots, v_n\). Ako je redni broj čvora \(s\) od koga treba odrediti najkraće puteve u topološkom redosledu jednak \(k\) (tj. ako je \(s \equiv v_k\)), onda se čvorovi sa rednim brojevima manjim od \(k\) ne moraju ni razmatrati, jer ne postoji način da se iz čvora \(s\) do njih dođe. Zato, jednostavnosti radi, pretpostavimo da je redni broj čvora \(s\) od koga treba izračunati najkraće puteve u topološkom redosledu \(1\), tj. da je \(s \equiv v_1\). Ako dodatno pretpostavimo da osim čvora \(s\) u grafu nema drugih čvorova čiji je ulazni stepen nula, tada možemo biti sigurni da će do svakog čvora postojati put od polaznog (u suprotnom, do nekih čvorova neće postojati put, pa za njih možemo pretpostaviti da je dužina najkraćeg puta jednaka \(+\infty\)). Redosled čvorova dobijen topološkim sortiranjem je pogodan za primenu indukcije, tj. sugeriše jednostavno rekurzivno rešenje, koje se zatim tehnikom dinamičkog programiranja može optimizovati i pretvoriti u efikasno iterativno rešenje.
Izlaz iz rekurzije nastupa kada se obrađuje čvor \(v_1\) i najkraći put od tog čvora do njega samog je dužine \(0\).
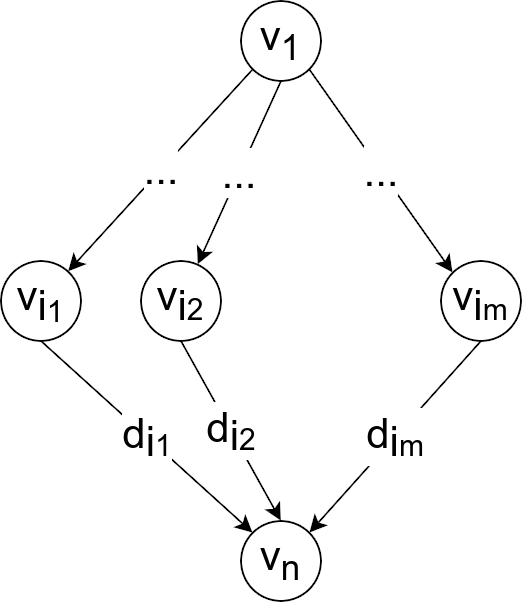
Posmatrajmo poslednji čvor u topološkom redosledu čvorova, odnosno čvor \(v_n\). Označimo dužinu najkraćeg puta od čvora \(s\) do proizvoljnog čvora \(v_i\) sa \(v_i.\mathit{SP}\) (engl. shortest path), a dužinu grane \((x,y)\) između proizvoljna dva čvora \(x\) i \(y\) sa \(d(x,y)\). Kako bismo odredili vrednost \(v_n.\mathit{SP}\), dovoljno je da proverimo samo one čvorove \(v_i\) iz kojih postoji grana do čvora \(v_n\), jer se najkraći put do čvora \(v_n\) mora završiti nekom od tih grana (slika 1).

Pošto se najkraći putevi do svih ostalih čvorova mogu odrediti rekurzivno, vrednost \(v_n.\mathit{SP}\) biće jednaka minimumu zbira \(v_i.\mathit{SP}+d(v_i,v_n)\), po svim čvorovima \(v_i\) iz kojih vodi grana do čvora \(v_n\):
\[v_n.\mathit{SP}=\min_{(v_i,v_n)\in E} \{v_i.\mathit{SP}+d(v_i,v_n)\}.\]
Da li je time problem rešen? Najkraći putevi do čvorova \(v_1, \ldots v_{n-1}\) su određeni bez razmatranja čvora \(v_n\). Važno pitanje je da li dodavanje čvora \(v_n\) u skup čvorova do kojih smo odredili najkraće puteve može da skrati najkraći put od \(v_1\) do nekog od njih, tj. da li je moguće da je najkraći put preko \(v_n\) kraći od najkraćeg puta koji ne vodi preko čvora \(v_n\). Međutim, pošto je \(v_n\) poslednji čvor u topološkom redosledu, ni jedan drugi čvor nije dostižan iz \(v_n\), pa se dužine ostalih najkraćih puteva ne menjaju. Dakle, uklanjanje čvora \(v_n\) iz grafa, pronalaženje najkraćih puteva u preostalom grafu, vraćanje čvora \(v_n\) nazad u graf i računanje rastojanja do njega su osnovni delovi algoritma.
Iz ovog razmatranja direktno sledi odgovarajući rekurzivni algoritam. Međutim, kao što je to čest slučaj sa rekurzivnim algoritmima, on može biti veoma neefikasan, usled ponovljenih rekurzivnih poziva (jer iz čvora može voditi više grana). Ovo se, naravno, optimizuje nekim oblikom dinamičkog programiranja. U ovom slučaju je zadatak bolje rešavati induktivno, tako što se čvorovi obrađuju u topološkom redosledu, najkraći put do početnog čvora se inicijalizuje na 0, dok se za svaki naredni čvor najkraći put računa primenom prikazane rekurentne formule. Ovo odgovara standardnoj tehnici dinamičkog programiranja naviše.
Grafovski algoritmi su često zasnovani na nekom obliku induktivno-rekurzivne konstrukcije tj. dinamičkog programiranja. U takvim problemima je svakom čvoru grafa potrebno pridružiti vrednost neke statistike (u našem primeru to je najkraći put od početnog čvora). Vrednost statistike čvora obično zavisi od vrednosti statistika njegovih suseda i često je najveći izazov u rešenju pronaći redosled obrade čvorova koji će omogućiti da su prilikom obrade nekog čvora statistike svih njegovih suseda ispravno izračunate tj. mogu biti izračunate rekurzivnim pozivima koji neće obuhvatiti poziv za čvor koji se trenutno obrađuje (jer bi se u tom slučaju upalo u beskonačnu rekurziju). U ovom primeru, to je omogućio topološki redosled. Pošto je čvor često sused većem broju čvorova, da bi se izbeglo višestruko izračunavanje njemu pridružene statistike, poželjno je koristiti ili memoizaciju (pamćenje vrednosti te statistike u čvoru ili posebnom nizu) ili dinamičko programiranje naviše (gde se vrednosti pamte na isti način).
U prethodno opisanom postupku je pre početka traženja najkraćih puteva potrebno izvrši topološko sortiranje grafa. Takođe, potrebno je za svaki čvor odrediti grane koje vode do njega, što nije efikasna operacija kada se koriste liste povezanosti (grane su usmerene od predaka ka potomcima u topološkom redosledu, a ne obratno). Pokušajmo sada da unapredimo algoritam za traženje najkraćih puteva u acikličkom grafu, tako da se algoritam za topološko sortiranje obavlja istovremeno sa pronalaženjem najkraćih puteva. Drugim rečima, cilj je objediniti dva prolaza kroz graf (jedan za topološko sortiranje i drugi za nalaženje najkraćih puteva) u jedan; pritom se sve vreme izračunavanja vrše induktivno, od predaka ka potomcima u topološkom redosledu.
Razmotrimo način na koji se algoritam rekurzivno izvršava (posle nalaženja topološkog redosleda). Prvi korak je poziv rekurzivne procedure za čvor \(v_n\). Procedura zatim poziva rekurzivno samu sebe, sve dok se ne dođe do čvora \(s \equiv v_1\). U tom trenutku se dužina najkraćeg puta od čvora \(s\) do čvora \(s\) postavlja na \(0\), i rekurzija počinje da se “razmotava”. Razmatra se čvor \(v_2\); dužina najkraćeg puta do njega izjednačuje se sa dužinom grane \((v_1, v_2)\), ako ona postoji; u protivnom, ne postoji put od \(v_1\) do \(v_2\). Sledeći korak je provera čvora \(v_3\). U čvor \(v_3\) ulaze najviše dve grane — od čvorova \(v_1\) i/ili \(v_2\), pa se upoređuju dužine odgovarajućih puteva. Umesto ovakvog izvršavanja rekurzije unazad, pokušaćemo da iste korake izvršimo unapred.
Indukcija se primenjuje prema rastućim rednim brojevima u topološkom redosledu počevši od \(s \equiv v_1\). Ovaj redosled oslobađa nas potrebe da redne brojeve unapred znamo, pa ćemo biti u stanju da izvršavamo istovremeno i algoritam za određivanje topološkog uređenja i algoritam za određivanje najkraćih puteva od čvora \(s\). Dakle, možemo razmotriti narednu induktivnu hipotezu.
Induktivna hipoteza. Znamo prvih \(k-1\) čvorova u topološkom redosledu čvorova i dužine najkraćih puteva od čvora \(s\) do njih.
Potrebno je da odredimo čvor \(v_k\) sa rednim brojem \(k\). To može da bude proizvoljni čvor u koji ne vodi ni jedna grana iz čvora sa rednim brojem većim od \(k\) (tj. bilo koji čvor stepena 0 kada se izbace sve grane iz prethodnih čvorova). Da bismo pronašli najkraći put do \(v_k\), moramo da proverimo sve grane koje vode u njega. Topološki redosled garantuje da sve takve grane polaze iz čvorova sa manjim rednim brojevima. Prema induktivnoj hipotezi ti čvorovi su poznati, kao i dužine najkraćih puteva do njih. Za svaku granu \((v_i, v_k)\) znamo dužinu \(v_i.\mathit{SP}\) najkraćeg puta od \(s\) do \(v_i\), pa je dužina najkraćeg puta od \(s\) do \(v_k\) preko \(v_i\) jednaka \(v_i.\mathit{SP}+d(v_i, v_k)\). Pored toga, kao i ranije, ne moramo da vodimo računa o eventualnim promenama najkraćih puteva ka čvorovima sa manjim rednim brojevima od \(k\), jer se do njih ne može doći iz čvora \(v_k\).
Da ne bismo za svaki čvor određivali iz kojih čvorova postoji grana ka njemu, jer to nije efikasna operacija u reprezentaciji grafa listama povezanosti, tokom izvršavanja algoritma možemo pamtiti dužine \(v.\overline{\mathit{SP}}\) trenutno poznatih najkraćih puteva do svih čvorova \(v\), uključujući i one sa većim rednim brojem od tekućeg čvora \(v_k\). Prilikom razmatranja čvora \(v_k\) potrebno je jedino razmotriti grane \((v_k, v_j)\) koje polaze iz njega, za čvor \(v_j\) proveriti da li je vrednost \(v_k.\overline{\mathit{SP}}+d(v_k,v_j)\) manja od \(v_{j}.\overline{\mathit{SP}}\), i ako jeste, ažurirati vrednost \(v_j.\overline{\mathit{SP}}\). Dakle umesto da granu grafa obrađujemo “unazad”, odnosno u trenutku kada obrađujemo njen završni čvor, mi je obrađujemo “unapred”, u trenutku kada obrađujemo njen polazni čvor. Primetimo da se te grane već obrađuju tokom Kanovog algoritma prilikom izbacivanja čvora \(v_k\), kada se smanjuju ulazni stepeni čvorova \(v_j\), pa ažuriranje najkraćih rastojanja možemo uraditi u istoj petlji. Pošto su pre obrade čvora \(v_k\) već obrađene sve grane do \(v_k\) iz prethodnih čvorova \(v_i\) i pošto je svaka od njih obrađivana u trenutku kada je već bilo poznato najkraće rastojanje do \(v_i\), prilikom obrade čvora \(v_k\) niz najkraćih rastojanja sadrži najkraće rastojanje do \(v_k\), tj. važi \(v_k.\mathit{SP} = v_k.\overline{\mathit{SP}}\). Naime, umesto da se algoritam određivanja minimuma pokrene u trenutku obrade čvora \(v_k\), on se malo po malo izvršavao tokom obrade prethodnih čvorova \(v_j\).
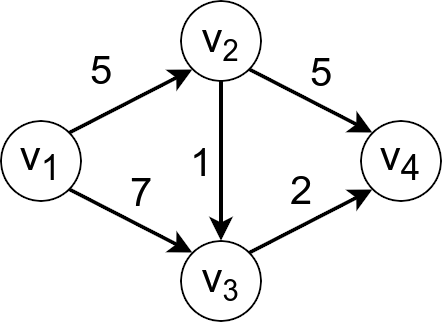
Primer 2.9.2. Razmotrimo izvršavanje algoritma na primeru acikličkog grafa sa slike 2. Redosled čvorova u topološkom poretku grafa je \(v_1, v_2, v_3, v_4\). Neka je zadatak odrediti najkraće puteve iz čvora \(s\equiv v_1\).
Na početku postavljamo vrednost \(v_1.\overline{\mathit{SP}}\) najkraćeg puta do čvora \(v_1\) na \(0\) (i to je konačna vrednost \(v_1.\mathit{SP}\) najkraćeg puta do čvora \(v_1\)), a vrednosti najkraćih puteva \(v_j.\overline{\mathit{SP}}\) do svih ostalih čvorova \(v_j\) na \(+\infty\).
Razmatramo grane koje polaze iz čvora \(v_1\): to su \((v_1,v_2)\) i \((v_1,v_3)\), i ažuriramo najkraće puteve do čvora \(v_2\) i do čvora \(v_3\) na \(v_2.\overline{\mathit{SP}}=\min\{+\infty,0+5\}=5\), a \(v_3.\overline{\mathit{SP}}=\min\{+\infty,0+7\}=7\).
Drugi čvor u topološkom redosledu je čvor \(v_2\): tekuću vrednost \(v_2.\overline{\mathit{SP}}\) najkraćeg puta do njega proglašavamo za konačnu vrednost najkraćeg puta, odnosno proglašavamo \(v_2.\mathit{SP}=5\).
Zatim razmatramo grane koje izlaze iz čvora \(v_2\): to su grane \((v_2,v_3)\) i \((v_2,v_4)\) i ažuriramo najkraće puteve do čvorova \(v_3\) i \(v_4\): \(v_3.\overline{\mathit{SP}}=\min\{7,5+1\}=6\) i \(v_4.\overline{\mathit{SP}}=\min\{+\infty,5+5\}=10\).
Treći po redu čvor u topološkom poretku je čvor \(v_3\) te tekuću vrednost \(v_3.\overline{\mathit{SP}}\) najkraćeg puta do njega proglašavamo za konačnu, odnosno proglašavamo \(v_3.\mathit{SP}=6\).
Razmatramo jedinu granu \((v_3,v_4)\) koja polazi iz čvora \(v_3\) i vršimo ažuriranje vrednosti \(v_4.\overline{\mathit{SP}}\) najkraćeg puta do čvora \(v_4\): \(v_4.\overline{\mathit{SP}}=\min\{10,6+2\}=8\).
U ovom trenutku proglašavamo kao konačnu i dužinu \(v_4.\overline{\mathit{SP}}\) najkraćeg puta do čvora \(v_4\), odnosno proglašavamo \(v_4.\mathit{SP} = 8\), čime se izvršavanje algoritma završava.
Iz prethodnog razmatranja sledi naredna teorema o korektnosti ovog algoritma.
Teorema 2.9.1. Neka je \(G = (V, E)\) usmeren aciklički težinski graf i \(v_1\) neki njegov čvor čiji je ulazni stepen 0. Ako se najkraća rastojanja inicijalizuju tako da je \(v_1.\overline{\mathit{SP}}=0\) i \(v_i.\overline{\mathit{SP}}=+\infty\), za svako \(1 < i \leq n=|V|\), tada se nakon sprovođenja algoritma dobija topološki redosled čvorova \(v_1, \ldots, v_n\) i za svaki čvor \(v_i \in V\) važi \(v_i.\overline{\mathit{SP}} = v_i.\mathit{SP}\), tj. niz sadrži najkraće rastojanje od čvora \(v_1\) do svih ostalih čvorova u grafu.
Do sada smo razmatrali izračunavanje dužina najkraćih puteva, a ne i računanje samih najkraćih puteva. Primetimo da smo najkraće puteve određivali jedan po jedan: svaki novi najkraći put se dobija produživanjem nekog prethodno određenog najkraćeg puta poslednjom granom na putu. Grane kojima se vrši produživanje formiraju tzv. drvo najkraćih puteva (engl. shortest-path tree). Kako bismo mogli da rekonstruišemo najkraće puteve do svakog čvora, za svaki čvor pamtimo njegovog prethodnika (roditelja) na najkraćem putu od čvora \(s\). Jedino čvor \(s\equiv v_1\) nema roditelja na najkraćem putu (ako čvor \(s\) nije prvi u topološkom redosledu, roditelje neće imati ni čvorovi koji su ispred njega u topološkom redosledu). Na taj način možemo jednostavno da rekonstruišemo same najkraće puteve.
U narednom apletu možete videti kako funkcioniše modifikacija Kanovog algoritma koja određuje najkraće puteve od čvora \(0\) do ostalih čvorova u acikličkom grafu.
Razmotrimo implementaciju algoritma: pretpostavićemo da je potrebno odrediti najkraće puteve od čvora \(0\) do svih ostalih čvorova. Pretpostavimo, jednostavnosti radi, i da je polazni čvor jedini čvor ulaznog stepena 0. Vrednosti \(+\infty\) ćemo u implementaciji predstavljati najvećim celim brojem koji može da se zapiše u tipu int. To olakšava implementaciju jer se izbegavaju grananja, ali treba biti obazriv da se taj broj tokom algoritma ne sabira sa drugim brojevima (inače bi došlo do prekoračenja).
// umesto vrednosti beskonacno koja oznacava da put nije pronađen
// koristimo najveći broj koji se može zapisati u tipu težine grana
const Tezina INF = numeric_limits<Tezina>::max();
// funkcija koja stampa put od polaznog cvora v do datog cvora
// kroz grane drveta najkracih puteva
void odstampajPutDoCvora(Cvor cvor, vector<Cvor> roditelji) {
// ako postoji put do roditeljskog cvora, stampamo ga
if (roditelji[cvor] != -1)
odstampajPutDoCvora(roditelji[cvor], roditelji);
// stampamo tekuci cvor
cout << " " << cvor;
}
// funkcija koja stampa najkraci put do datog cvora i njegovu duzinu
void odstampajNajkraciPut(Cvor cvor, vector<Cvor> roditelji,
vector<Tezina> minRastojanja) {
cout << "Najkraci put do cvora " << cvor << " je:";
odstampajPutDoCvora(cvor, roditelji);
cout << " i duzine je " << minRastojanja[cvor] << endl;
}
// funkcija koja racuna najkrace puteve od cvora 0 u aciklickom grafu
void aciklicki_najkraci_putevi() {
int brojCvorova = listaSuseda.size();
// niz koji za svaki cvor cuva njegov ulazni stepen
vector<int> ulazniStepeni(brojCvorova, 0);
// niz koji za svaki cvor cuva duzinu
// trenutno poznatog najkraceg puta do njega
vector<Tezina> minRastojanja(brojCvorova, INF);
// niz koji za svaki cvor cuva roditelja u najkracem putu
vector<Cvor> roditelji(brojCvorova, -1);
// najkraci put od cvora 0 do njega samog postavljamo na 0
minRastojanja[0] = 0;
// inicijalizujemo niz ulaznih stepena cvorova
// potreban za izvršavanje Kanovog algoritma
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
for (const auto& [sused, tezina] : listaSuseda[cvor])
ulazniStepeni[sused]++;
// red koji cuva cvorove ulaznog stepena nula
queue<Cvor> cvoroviStepenaNula;
// pretpostavljeno je da je polazni cvor 0 jedini stepena 0
cvoroviStepenaNula.push(0);
while(!cvoroviStepenaNula.empty()) {
// cvor sa pocetka reda je naredni u topoloskom redosledu
Cvor cvor = cvoroviStepenaNula.front();
cvoroviStepenaNula.pop();
// do njega je odredjen najkraci put i stampamo ga
odstampajNajkraciPut(cvor, roditelji, minRastojanja);
for (const auto& [sused, tezina] : listaSuseda[cvor]) {
// ukoliko je do nekog cvora kraci put preko upravo razmatranog cvora
// vrsimo azuriranje najkraceg rastojanja do tog cvora
if (minRastojanja[cvor] + tezina < minRastojanja[sused]) {
minRastojanja[sused] = minRastojanja[cvor] + tezina;
// azuriramo koji je roditeljski cvor na najkracem putu
roditelji[sused] = cvor;
}
ulazniStepeni[sused]--;
// ukoliko je stepen nekog od suseda pao na 0, dodajemo ga u red
if (ulazniStepeni[sused] == 0)
cvoroviStepenaNula.push(sused);
}
}
}U algoritmu se svaka grana razmatra po jednom u toku inicijalizacije ulaznih stepena čvorova, i po jednom u trenutku kad se njen polazni čvor uklanja iz reda. Pristup redu zahteva konstantno vreme. Svaki čvor se razmatra tačno jednom. Prema tome, vremenska složenost algoritma za određivanje najkraćih puteva u acikličkom grafu je u najgorem slučaju \(O(|V|+|E|)\).
Kad graf nije aciklički, ne postoji topološki redosled, pa se razmatrani algoritam ne može direktno primeniti. Međutim, osnovne ideje se mogu iskoristiti i u opštem slučaju, doduše, samo kod grafova kod kojih su dužine grana nenegativne. Naime, jednostavnost algoritma za određivanje najkraćih puteva iz zadatog čvora u acikličkom grafu posledica je sledeće osobine topološkog redosleda: ako je \(v_k\) čvor sa rednim brojem \(k\) u topološkom poretku, onda:

Ova osobina topološkog redosleda omogućuje nam da organizujemo redosled rekurzivnih tj. induktivnih izračunavanja tj. da nađemo najkraći put od čvora \(s\equiv v_1\) do čvora \(v_k\), ne vodeći računa o čvorovima koji su posle \(v_k\) u topološkom redosledu (jer od njih sigurno ne postoje putevi do \(v_k\)). Može li se nekako definisati redosled čvorova proizvoljnog grafa (koji nije nužno aciklički) koji bi omogućio nešto slično?
Ključna ideja je razmatrati čvorove grafa redom prema dužinama najkraćih puteva od čvora \(s\) do njih. Naime, ako se čvorovi urede u niz \(v_1,v_2,\ldots,v_n\) neopadajuće na osnovu dužina tih puteva, i ako u grafu nema grana negativne težine, važe veoma slična svojstva kao kod topološkog poretka:
Dakle, prilikom određivanja najkraćeg puta do \(v_k\) mogu se zanemariti putevi koji vode preko čvorova sa rednim brojevima većim od \(k\), tj. treba razmotriti samo puteve preko čvorova sa rednih brojeva manjih od \(k\), koji mogu mogu biti određeni rekurzivno tj. induktivno. Ako bismo unapred mogli da odredimo ovaj redosled čvorova, rekurzivni algoritam bi mogao da funkcioniše po istom principu kao i u slučaju acikličkih grafova. Izbacili bismo čvor \(v_n\) koji je najudaljeniji od čvora \(s \equiv v_1\), izračunali rastojanja od \(s\) do svih ostalih čvorova, a zatim bismo analizirali grane \((v_i, v_n)\) i rastojanje do \(v_n\) odredili kao \(\min_{(v_i, v_n) \in E}\{v_i.\mathit{SP} + d(v_i, v_n)\}\). Zahvaljujući prethodnim uslovima znamo da grane koje vode iz \(v_n\), nazad ka prethodnim čvorovima ne treba razmatrati, tj. da određivanje najkraćeg rastojanja do \(v_n\) ne može ni na koji način ažurirati najkraća rastojanja prethodnih čvorova (ona će biti ispravno određena i pre razmatranja čvora \(v_n\)). Izlaz iz ovog rekurzivnog postupka je slučaj \(v_1 \equiv s\) (jer je najbliži čvor početnom čvoru \(s\) upravo čvor \(s\)) kada je najkraće rastojanje jednako \(0\).
Međutim, algoritam moramo organizovati drugačije, jer se, naravno, dužine puteva, pa ni ovaj poredak na početku ne znaju, već se izračunavaju u toku izvršavanja algoritma.
Pošto su sve grane nenegativne dužine, najkraće rastojanje od čvora \(s\) do čvora \(s\) je \(0\) i čvor \(s\) je prvi u ovom redosledu. Dakle, ponovo važi \(s \equiv v_1\).
Nakon toga proveravamo sve grane koje izlaze iz čvora \(v_1\). Neka je \((v_1,v_2)\) najkraća među njima. Pošto su, po pretpostavci, sve dužine grana nenegativne, najkraći put od čvora \(s\) do čvora \(v_2\) je grana \((v_1, v_2)\). Dužine svih drugih puteva od čvora \(s\) do čvora \(v_2\) su veće ili jednake od dužine ove grane. Čvor \(v_2\) je, dodatno, najbliži od svih čvorova čvoru \(s\). Prema tome, znamo najkraći put do čvora najbližeg čvoru \(s\).
Pokušajmo da napravimo sledeći korak. Kako možemo da pronađemo čvor do koga vodi naredni najkraći put, odnosno da odredimo čvor \(v_3\) koji je treći najbliži čvoru \(s\) (\(v_1 \equiv s\) i \(v_2\) su prva dva najbliža). Jedini putevi koje treba uzeti u obzir su preostale grane iz čvora \(v_1\) (koje ne vode do \(v_2\)) ili putevi koji se sastoje od dve grane, tako da je prva grana \((v_1, v_2)\), a druga je neka grana koja polazi iz čvora \(v_2\). Ostali putevi mogu biti samo duži od ovih. Čvor \(v_3\), dakle, određujemo kao onaj čvor \(v_i\) različit od \(v_1\) i \(v_2\) za koji je najmanja vrednost \(\min\{d(v_1, v_i),d(v_1, v_2)+d(v_2, v_i)\}\).
Sličan se postupak koristi i za određivanje narednih čvorova.
Primer 2.9.3. Razmotrimo graf sa slike 4 i problem traženja najkraćih puteva od čvora \(v\).
Može se formulisati sledeća induktivna hipoteza.
Induktivna hipoteza. Za zadati graf \(G=(V,E)\) i njegov čvor \(s\), umemo da odredimo \(k\) čvorova najbližih čvoru \(s\), kao i dužine najkraćih puteva do njih.
Zapazimo da se indukcija primenjuje po broju čvorova do kojih su dužine najkraćih puteva već izračunate, a ne po veličini grafa. Pored toga, pretpostavlja se da su to čvorovi najbliži čvoru \(s\), i da umemo da ih odredimo. Čvor \(s\) je najbliži sam sebi i na rastojanju je 0, pa je baza (slučaj \(k=1\)) rešena. Kad \(k\) dostigne vrednost \(|V|\), rešen je kompletan problem. Ako se ne traže rastojanja do svih čvorova, nego samo do nekog istaknutog čvora \(v'\), postupak se može prekinuti i ranije, čim se izračuna rastojanje do čvora \(v'\).
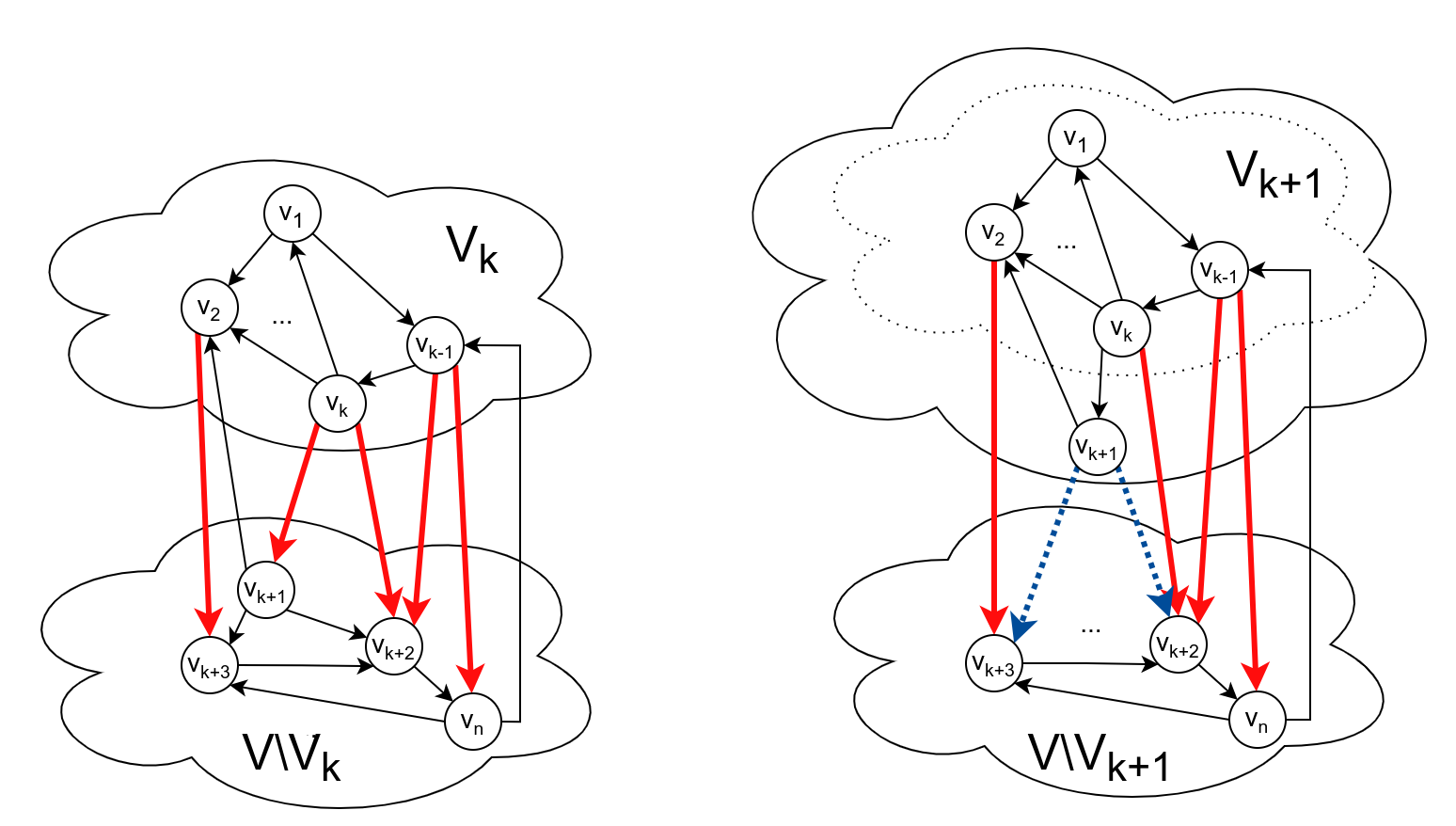
Označimo sa \(V_k = \{v_1, \ldots, v_k\}\) skup koji se sastoji od \(k\) najbližih čvorova čvoru \(s\) (uključujući i \(s\equiv v_1\)). Problem je pronaći čvor \(v_{k+1}\) koji je najbliži čvoru \(s\) među čvorovima van \(V_k\), i pronaći najkraći put od \(s\) do \(v_{k+1}\).
Najkraći put od \(s\) do \(v_{k+1}\) može da sadrži samo čvorove iz \(V_k\). On ne može da sadrži neki čvor \(v\) van \(V_k\), jer bi u tom slučaju čvor \(v\) bio bliži čvoru \(s\) od čvora \(v_{k+1}\), ako su težine grana pozitivne. Ako eventualno postoje grane težine nula, za čvor \(v_{k+1}\) ćemo odabrati neki od onih čvorova van \(V_k\) do kojih najkraći put prolazi samo kroz čvorove iz \(V_k\) (bar jedan takav čvor mora da postoji). Prema tome, da bismo pronašli čvor \(v_{k+1}\), dovoljno je da proverimo grane koje spajaju čvorove iz \(V_k\) sa čvorovima koji nisu u \(V_k\); sve druge grane se za sada mogu ignorisati. Neka je \((v_i,v)\) proizvoljna grana grafa \(G\) takva da je \(v_i\in V_k\) i \(v\notin V_k\). Takva grana određuje put od \(s\) do \(v\) koji se sastoji od najkraćeg puta od \(s\) do \(v_i\) (koji je prema induktivnoj hipotezi već poznat) i grane \((v_i,v)\). Dovoljno je uporediti dužine svih takvih puteva i izabrati najkraći među njima (slika 5, levo).
Algoritam određen ovom induktivnom hipotezom izvršava se na sledeći način. U svakoj iteraciji u skup \(V_k\) se dodaje novi čvor. U prvoj je to čvor \(s\). U svakoj narednoj iteraciji je to onaj čvor \(v\notin V_k\) koji je najbliži čvoru \(s\), tj. za koji je najmanja vrednost izraza:
\[\min \left\{v_i.\mathit{SP}+d(v_i,v) \right| v_i\in V_k\}.\](1)
Iz već iznetih razloga, tako odabrani čvor \(v\) je zaista \((k+1)\)-vi (sledeći) najbliži čvor čvoru \(s\), pa ga možemo obeležiti sa \(v_{k+1}\). Formulom (1) određena je i stvarna dužina najkraćeg puta od čvora \(s\) do čvora \(v_{k+1}\) (ona se neće dalje smanjivati). Prema tome, dodavanje čvora \(v_{k+1}\) skupu \(V_k\) proširuje induktivnu hipotezu.
Algoritam je sada u potpunosti preciziran, ali mu se efikasnost može poboljšati. Osnovni korak algoritma je pronalaženje sledećeg najbližeg čvora \(v_{k+1}\) čvoru \(s\). To se ostvaruje izračunavanjem dužine najkraćeg puta (preko čvorova iz \(V_k\)) do svakog čvora \(v \notin V_k\) prema formuli (1). Možemo da, kao i u slučaju acikličkog grafa, u nizu pamtimo dužine \(v.\overline{\mathit{SP}}\) trenutno poznatih najkraćih puteva do svih čvorova \(v\in V\), a da im pri proširivanju skupa \(V_k\) ažuriramo vrednosti. Za čvorove van \(V_k\) to će biti najkraći putevi koji vode isključivo preko čvorova u \(V_k\), tj. preko svih grana koje polaze iz čvorova u \(V_k\), a ne i globalno najkraći, jer možda do njih postoji i neki kraći put koji vodi preko čvorova van \(V_k\), pa uključuje i neke do sada nepregledane grane.
Vrednosti \(v.\overline{\mathit{SP}}\) za čvorove van \(V_k\) se menjaju prilikom proširivanja skupa \(V_k\) (koji figuriše u formuli (1)). Ipak, realno je očekivati da proširivanje skupa \(V_k\) čvorom \(v_{k+1}\) ne utiče na vrednost rastojanja mnogih čvorova \(v \notin V_k\). Zaista, mogu se promeniti samo vrednosti za one čvorove \(v\) do kojih postoji grana \((v_{k+1}, v)\), tj. samo one vrednosti koje odgovaraju putevima kroz novododati čvor \(v_{k+1}\). Prema tome, prilikom dodavanja čvora \(v_{k+1}\) u skup \(V_k\) treba proveriti sve grane od čvora \(v_{k+1}\) ka čvorovima van \(V_k\) (slika 5, desno). Za svaku takvu granu \((v_{k+1}, v)\) upoređujemo zbir \(v_{k+1}.\overline{\mathit{SP}} + d(v_{k+1}, v)\) sa trenutnom vrednošću \(v.\overline{\mathit{SP}}\), i po potrebi ažuriramo (smanjujemo) vrednost \(v.\overline{\mathit{SP}}\). Primetimo da smo isti ovaj način ažuriranja koristili i za izračunavanje najkraćih puteva u acikličkom grafu. Svaka iteracija algoritma, dakle, obuhvata nalaženje čvora \(v\equiv v_{k+1}\) van \(V_k\) sa najmanjom trenutnom vrednošću \(v.\overline{\mathit{SP}}\), i eventualno ažuriranje vrednosti \(v.\overline{\mathit{SP}}\) za njegove susede koji nisu u \(V_k\). Pošto su prilikom izbora tog čvora \(v_{k+1}\) već obrađene sve grane koje vode do njega od čvorova \(v_i\) koji su bliži čvoru \(s\) od njega i pošto se na najkraćem putu do njega ne može naći nijedan drugi čvor van \(V_k\), tekuća vrednost \(v_{k+1}.\overline{\mathit{SP}}\) se poklapa sa stvarnom vrednošću \(v_{k+1}.\mathit{SP}\) najkraćeg rastojanja do njega.
Ovaj algoritam dobio je naziv Dajkstrin algoritam (engl. Dijkstra’s algorithm) po Edzgaru Dajkstri koji ga je osmislio 1956. godine. On pripada grupi pohlepnih algoritama, jer se u svakom koraku bira lokalno optimalno rešenje – najbliži čvor i nakon obrade trenutno najbližeg čvora rastojanje do njega se više nikada ne razmatra.
Najkraće puteve od čvora \(s\) do svih ostalih čvorova našli smo tako što smo pronalazili jedan po jedan najkraći put. Svaki novi put je određen jednom granom, koja produžuje prethodno poznati najkraći put do novog čvora. Sve te grane – produžeci puteva formiraju drvo sa korenom u čvoru \(s\). Ovo drvo naziva se drvo najkraćih puteva i važno je za rešavanje mnogih problema sa putevima. Primetimo da ako bi dužine svih grana u grafu bile međusobno jednake, onda bi drvo najkraćih puteva u stvari bilo BFS drvo sa korenom u čvoru \(s\).
Prethodnim razmatranjem smo dokazali narednu teoremu.
Teorema 2.9.2. Neka je dat težinski graf \(G=(V, E)\) u kom su težine svih grana nenegativne i neka je \(s \in V\). Neka su u startu čvorovima pridružene vrednosti tako da je \(s.\overline{\mathit{SP}} = 0\) i \(v.\overline{\mathit{SP}} = +\infty\), za svako \(v \in V\), \(v \neq s\). Nakon što se ponovi \(n\) koraka Dajkstrinog algoritma, tj. nakon što se svaki čvor grafa ubaci u skup \(V_k\), za svaki čvor \(v \in V\) biće ispravno određen najkraći put od \(s\), tj. važiće \(v.\mathit{SP} = v.\overline{\mathit{SP}}\).
Primer 2.9.4. Izvršavanje Dajkstrinog algoritma za nalaženje najkraćih puteva od čvora \(v\) ilustrovano je na slici 6.
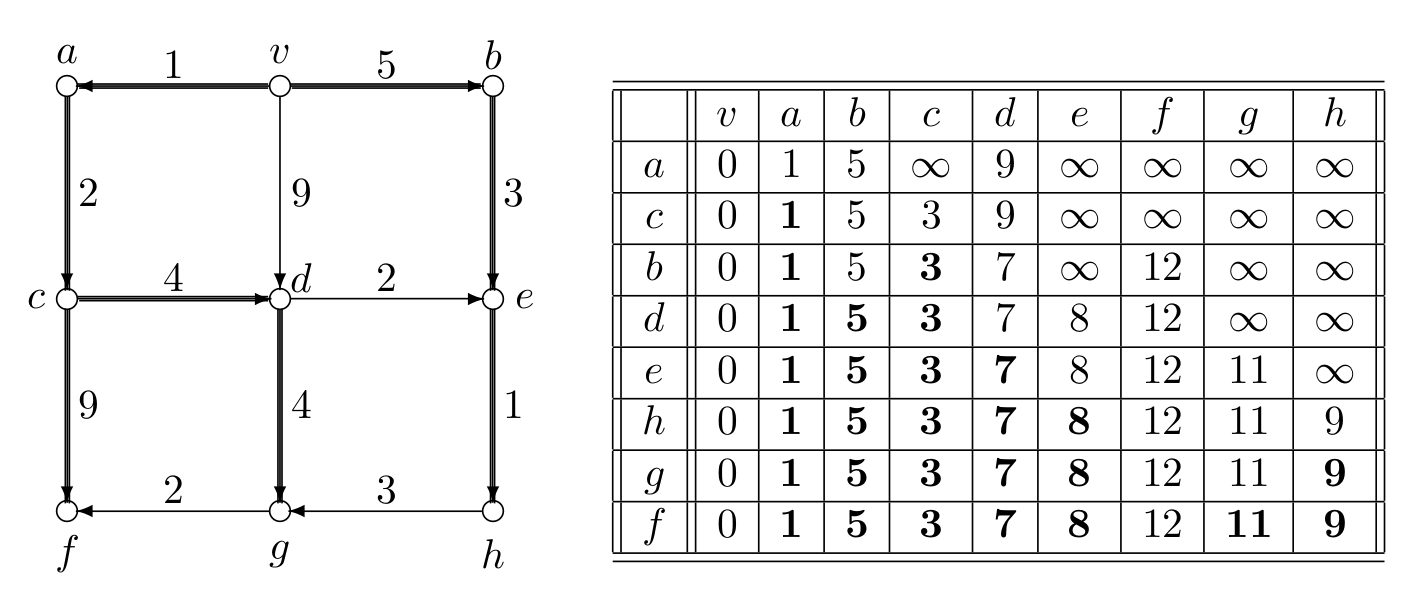
U primeru na slici 6 podebljane su grane koje pripadaju drvetu najkraćih puteva od čvora \(s \equiv v\), sa korenom u čvoru \(v\). Primetimo da, recimo, najkraći put do čvora \(h\) dobijamo tako što granom \((e,h)\) produžimo prethodno pronađeni najkraći put do čvora \(e\): put \((v,b,e)\).
Tabela registruje promene u nizu \(\overline{\mathit{SP}}\) u kom se čuvaju dužine najkraćih puteva od čvora \(v\) do svih ostalih čvorova preko čvorova koji pripadaju skupu \(V_k\). Elementi skupa \(V_k\) (pored čvora \(v\)) su oni čije su dužine najkraćih puteva ispisane podebljano (to su konačne dužine najkraćih puteva).
Prva vrsta tabele odnosi se samo na puteve koji se sastoje od jedne grane koja polazi iz čvora \(v\). Bira se najkraći od tih puteva (grana) i u ovom slučaju on vodi ka čvoru \(a\).
Druga vrsta tabele pokazuje ažuriranje dužina najkraćih puteva uključujući sada sve puteve koji se sastoje od jedne grane koja polazi iz čvora \(v\) ili od dve grane preko čvora \(a\). Drugi najkraći put od čvora \(v\) vodi do čvora \(c\).
U svakom koraku algoritma bira se novi, naredni najbliži čvor čvoru \(v\), dodaje se u skup \(V_k\) i u narednoj vrsti tabele se prikazuju dužine trenutnih najkraćih puteva od čvora \(v\) do svih čvorova.
Na osnovu tabele moguće je rekonstruisati i same najkraće puteve. Na primer, ako želimo da saznamo koji je najkraći put od čvora \(v\) do čvora \(h\) dužine \(9\), razmatramo kolonu koja odgovara čvoru \(h\) i tražimo poslednju promenu vrednosti u toj koloni – ona odgovara vrsti označenoj čvorom \(e\) i to znači da je čvor \(e\) roditelj čvora \(h\) u drvetu najkraćih puteva. Zatim, na osnovu tabele određujemo roditelja čvora \(e\), gledajući kolonu tabele koja odgovara čvoru \(e\) i utvrđivanjem na kom čvoru se desila poslednja promena vrednosti u ovoj tabeli – to je čvor \(b\) te je on roditelj čvora \(e\), dok je roditelj čvora \(b\) polazni čvor \(v\). Konačno, najkraći put rekonstruišemo čitajući dobijeni niz roditeljskih čvorova unazad i kao najkraći put od čvora \(v\) do čvora \(h\) dobijamo put \((v,b,e,h)\). Naravno, umesto da pamtimo celu tabelu, efikasnije je da roditeljske čvorove održavamo u zasebnom nizu.
Naredni aplet prikazuje redosled obrade čvorova u Dajkstrinom algoritmu.
U narednom apletu možete proveriti svoje razumevanje Dajkstrinog algoritma, ali i videti simulaciju njegovog izvršavanja.
U Dajkstrinom algoritmu potrebno je da \(O(|V|)\) puta pronalazimo dužine najkraćih puteva do čvorova van skupa \(V_k\) i da često ažuriramo dužine puteva. Struktura podataka pogodna za efikasno nalaženje minimalnih elemenata je red sa prioritetom. Pretpostavićemo da je on realizovan kao min-hip (mada može biti realizovan i pomoću balansiranog binarnog drveta, kao uređen skup). Pošto je potrebno da pronađemo čvor do koga je dužina puta najmanja, sve čvorove \(v\) van skupa \(V_k\) čuvamo u redu sa prioritetom, sa ključevima \(v.\overline{\mathit{SP}}\) jednakim dužinama trenutno najkraćih puteva od čvora \(s\) do njih. Na početku su sve dužine puteva osim one do čvora \(s\) jednake \(+\infty\), pa redosled elemenata u hipu nije bitan, sem što je čvor \(s\) na vrhu. Nalaženje čvora \(v_{k+1}\) koji je među čvorovima van \(V_k\) najbliži čvoru \(s\) je jednostavno: on se uzima sa vrha hipa. Posle toga se za svaku granu \((v_{k+1}, v)\) proverava da li je \(v\) van \(V_k\) i da li najkraći put do čvora \(v_{k+1}\) produžen granom \((v_{k+1}, v)\) skraćuje trenutno poznati najkraći put do čvora \(v\).
Međutim, kad se promeni dužina puta \(v.\overline{\mathit{SP}}\) do nekog čvora \(v\), potrebno je da se promeni i položaj čvora \(v\) u hipu. Prema tome, potrebno je na odgovarajući način popravljati hip. S obzirom na to da se putevi do čvora mogu samo skraćivati, to znači da se vrednost ključa u hipu može samo smanjiti i eventualno pri tom postati manja od vrednosti ključa svog roditelja (pošto je prethodna vrednost elementa bila manja od vrednosti njegove dece u hipu, to će važiti i za smanjenu vrednost ključa). Operacija smanjivanja vrednosti ključa u min-hipu nije direktno podržana u standardnoj biblioteci jezika C++, ali se odgovarajuća popravka hipa može ručno implementirati razmenom vrednosti elementa i njegovog roditelja, sve dok uslov hipa ne bude zadovoljen. Ova operacija se dakle može izvesti algoritmom složenosti \(O(\log n)\), gde je \(n\) broj elemenata u hipu. Međutim, problem sa ovim popravkama je u tome što hip kao struktura podataka ne podržava efikasno pronalaženje zadatog elementa. Naime, traženje elementa u hipu je operacija linearne vremenske složenosti u odnosu na broj elemenata u hipu. U ručnoj implementaciji bismo mogli u posebnom nizu čuvati položaj svakog čvora u hipu. Ipak, postoji jednostavan način da se ovo izbegne i da se upotrebi samo osnovni interfejs reda sa prioritetom (dodavanje elemenata, pronalaženje i brisanje najmanjeg elementa). Naime, umesto da se vrednost rastojanja do nekog čvora u hipu zameni novom (manjom) vrednošću, vrši se umetanje novog čvora sa istom oznakom čvora i novom (manjom) vrednošću rastojanja (ova tehnika se naziva tehnikom lenjog brisanja (engl. lazy deletion technique)). S obzirom na to da je nova vrednost rastojanja manja od stare, novi čvor će sigurno biti skinut iz hipa pre starog. Ostaje problem što će se u nekom kasnijem trenutku iz hipa skinuti i stari podatak o čvoru \(v\) sa većom vrednošću najkraćeg puta. Taj podatak treba da se zanemari, pa je prilikom uzimanja elementa sa vrha hipa potrebno prosto preskočiti čvorove koji su ranije bili obrađeni tj.
koji se već nalaze u skupu \(V_k\).
Ostaje bojazan da ovakva implementacija može da poveća vremenska složenost algoritma. Ukoliko bismo vršili popravke ključeva u hipu, u hipu bismo čuvali u svakom trenutku najviše \(O(|V|)\) elemenata. U implementaciji koja čuva kopije čvorova prilikom obrade svake (usmerene) grane može se dodati maksimalno jedan novi element u hip. Dakle ukupan broj elemenata u hipu biće sigurno manji ili jednak od \(O(|V| + |E|)\), te će svaka od operacija umetanja elementa u hip i brisanja minimalnog elementa iz hipa biti složenosti \(O(\log (|V| + |E|))\). S obzirom na to da je \(|E|\le |V|^2\), i stoga \(\log|E|\le 2\cdot \log|V|\), složenosti \(O(\log|E|)\) i \(O(\log |V|)\) se asimptotski ne razlikuju, te će operacije nad hipom koji čuva kopije čvorova biti iste asimptotske složenosti kao i u slučaju kada nema kopija. Naravno, memorijsko zauzeće može biti veće.
Dajkstrin algoritam za nalaženje najkraćih puteva od datog čvora prikazan je u nastavku.
// Dajkstrin algoritam za odredjivanje najkracih puteva
// iz datog polaznog cvora start do svih cvorova u grafu
void najkraciPuteviDajkstra(int start) {
int brojCvorova = listaSuseda.size();
// da li je cvoru odredjeno najkrace rastojanje
vector<bool> resen(brojCvorova, false);
// duzina trenutno poznatog najkraceg puta do cvora
vector<Tezina> minRastojanja(brojCvorova, INF);
// roditeljski cvor svakog cvora u drvetu najkracih puteva
vector<Cvor> roditelji(brojCvorova, -1);
// uredjen par koji čine rastojanje do cvora i broj cvora;
// redosled elemenata mora biti ovakav zbog operacije poredjenja parova
typedef pair<Tezina, Cvor> RastojanjeCvora;
// min-hip u koji smestamo poznata rastojanja do svih cvorova
priority_queue<RastojanjeCvora,
vector<RastojanjeCvora>,
greater<RastojanjeCvora>> rastojanja;
// ubacujemo polazni cvor u hip i postavljamo rastojanje do njega na 0
rastojanja.emplace(0, start);
minRastojanja[start] = 0;
// broj cvorova do kojih je konacno odredjeno najkrace rastojanje
int brojResenih = 0;
// dok se ne odredi najkrace rastojanje do svih cvorova
while (brojResenih < brojCvorova) {
// izdvajamo naredni najblizi cvor
auto [rastojanje, cvor] = rastojanja.top();
rastojanja.pop();
// ako je taj cvor ranije resen, preskacemo ga
// ovo se moze desiti zbog lenjog azuriranja hipa
if (resen[cvor])
continue;
// inace pamtimo da smo sada odredili najkrace rastojanje do njega
brojResenih++;
resen[cvor] = true;
// stampamo informaciju o najkracem putu do tog cvora;
// najkraci putevi se ispisuju u redosledu njihovog "otkrivanja"
odstampajNajkraciPut(cvor, roditelji, minRastojanja);
// prolazimo kroz sve grane iz tekuceg cvora
for (const auto& [sused, tezina] : listaSuseda[cvor]) {
// koje vode ka susedima kojima jos nije odredjeno najkrace rastojanje
if (!resen[sused]) {
// ukoliko je put kroz tekuci cvor do suseda kraci od poznatog
// najkraceg puta, azuriramo vrednost najkraceg puta do suseda
// i vrednost njegovog roditeljskog cvora
if (minRastojanja[cvor] + tezina < minRastojanja[sused]) {
minRastojanja[sused] = minRastojanja[cvor] + tezina;
roditelji[sused] = cvor;
// ubacujemo element u hip;
// ako je postojala prethodna vrednost, ne brisemo je:
// nova vrednost ce se naci u hipu iznad stare
rastojanja.emplace(minRastojanja[sused], sused);
}
}
}
}
}Kao što smo već pomenuli, operacije umetanja i brisanja iz hipa su složenosti \(O(\log |V|)\). Možemo imati najviše \(O(|V|+|E|)\) umetanja u hip (u varijanti sa čuvanjem kopija čvorova) i najviše \(O(|V|+|E|)\) brisanja iz hipa. Prema tome, vremenska složenost algoritma je \(O((|V| +|E|)\log |V|)\). Zapaža se da je Dajkstrin algoritam sporiji nego algoritam koji određuje najkraće puteve od zadatog čvora u acikličkom grafu. Ukoliko bi se umesto binarnog hipa koristio Fibonačijev hip, vremenska složenost Dajkstrinog algoritma bila bi jednaka \(O(|E|+|V|\log |V|)\). Napomenimo da je kod gustih grafova, kod kojih je broj grana asimptotski jednak \(|V|^2\), umesto hipa efikasnije koristiti običan niz i minimum tražiti linearnom pretragom (složenost je tada \(O(|V|^2)\), dok je složenost varijante sa hipom \(O(|V|^2\log{|V|})\).
Tip pretrage koji se javlja u Dajkstrinom algoritmu se naziva i pretraga sa prioritetom — svakom čvoru dodeljuje se prioritet (u ovom slučaju trenutno najmanje poznato rastojanje od polaznog čvora), pa se čvorovi obilaze redosledom koji je određen prioritetom. Kad se završi razmatranje tekućeg čvora, razmatraju se sve njemu susedne grane i pritom se mogu promeniti prioriteti nekih drugih čvorova. Način izvođenja tih promena je detalj po kome se jedna pretraga sa prioritetom razlikuje od druge. Pretraga sa prioritetom je karakteristična za težinske grafove i složenija je od obične pretrage za faktor \(\log |V|\) ako se koristi hip.
Razmotrimo sada problem određivanja najkraćih puteva iz zadatog čvora u opštem slučaju, kada težine grana mogu biti i negativne. Prirodno je zapitati se da li negativne težine grana imaju ikakvog smisla. U kontekstu rastojanja na mapama nemaju, međutim pokazuje se da težinski grafovi čije težine mogu biti i pozitivne i negativne nisu neuobičajeni u modelovanju nekih problema iz realnog sveta:
Na ovaj način možemo modelovati problem održavanja salda na računu: čvorovi grafa odgovaraju računima, grane transakcijama nad računima, pri čemu izvršavanje transakcije može dovesti do zarade – koju ćemo modelovati granom pozitivne težine ili do gubitka – koji ćemo modelovati granom negativne težine.
Problem putovanja iz jednog grada u drugi, pri čemu je moguće na nekom od delova puta pokupiti nekog putnika i zaraditi određenu količinu novca, može se modelovati na ovaj način. Cilj je stići iz jednog grada u drugi sa najviše novca na kraju. Ovaj problem možemo modelovati u vidu problema traženja najkraćeg puta u grafu čije težine grana mogu biti pozitivne i odgovaraju troškovima putovanja između ta dva grada (ako na tom delu puta putujemo sami) ili negativne (ako na nekom delu puta pokupimo jednog ili više putnika i od njih zaradimo više novca nego što su troškovi tog dela puta).
Nalaženje puta sa najmanjim proizvodom težina grana se može svesti na nalaženje puta sa najmanjim zbirom težina grana u grafu u kom je težina svake grane zamenjena njenim logaritmom (jer je logaritam monotona funkcija, a logaritam proizvoda jednak je zbiru logaritama). Primetimo da nakon logaritmovanja neke težine grana mogu postati negativne, pa se ponovo susrećemo sa problemom najkraćeg puta u grafu sa negativnim težinama grana.
Ukoliko graf sadrži neku granu negativne težine, Dajkstrin algoritam ne garantuje da ćemo do svakog čvora odrediti zaista najkraće puteve.
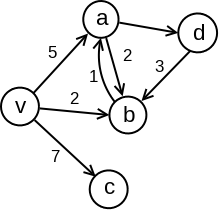
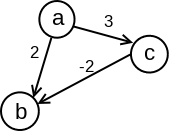
Primer 2.9.5. Razmotrimo problem određivanja najkraćih puteva iz čvora \(a\) do svih ostalih čvorova u grafu prikazanom na slici 7. Ako bismo primenili Dajkstrin algoritam, on bi najpre odredio najkraći put do čvora \(b\) (kao čvora koji je od svih čvorova do kojih postoji grana iz \(a\) najbliži čvoru \(a\)) i proglasio bi da je on dužine \(2\), a nakon toga bi odredio najkraći put do čvora \(c\) kao drugog najbližeg čvora čvoru \(a\) i proglasio bi da je dužina najkraćeg puta do njega \(3\) čime bi se se izvršavanje algoritma završilo. Jasno je da najkraći put od čvora \(a\) do čvora \(b\) vodi preko čvora \(c\) i dužine je \(1\), međutim Dajkstrin algoritam ne bi razmatrao ovaj put.
U nastavku teksta ćemo često pretpostavljati da graf ne sadrži ciklus negativne težine. Ovaj uslov je prirodan jer inače do nekih čvorova ne mora da postoji najkraći put (jer put možemo uvek dodatno skratiti još jednim prolaskom kroz ciklus). Možemo definisati da je najkraće rastojanje do takvih čvorova \(-\infty\) (iako je put uvek konačan, pa mu dužina ne može biti \(-\infty\)).
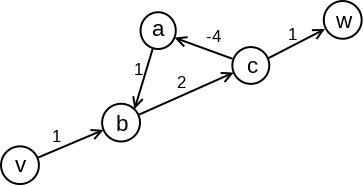
Primer 2.9.6. Razmotrimo graf sa slike 8: najkraći put od čvora \(v\) do čvora \(w\) se ne može odrediti jer svaki prolazak kroz ciklus \((b, c, a, b)\) smanjuje dužinu puta za \(1\) (dužina najkraćeg puta je \(-\infty\)).
Osnovni korak u algoritmu zasnovanom na relaksacijama grana je isti kao i u Dajkstrinom algoritmu i u algoritmu za određivanje najkraćih puteva u acikličkim grafovima, a to je tzv. relaksacija grane \((u,v)\), odnosno provera da li je vrednost \(v.\overline{\mathit{SP}}\) trenutno najkraćeg utvrđenog rastojanja od početnog čvora \(s\) do čvora \(v\) veća od vrednosti \(u.\overline{\mathit{SP}}+d(u,v)\); ako je to tačno, kažemo da je relaksacija uspešna, ažurira se vrednost \(v.\overline{\mathit{SP}}\) i pamti da najkraći put do čvora \(v\) vodi kroz čvor \(u\).
Zapravo, svi algoritmi za rešavanje ovog problema mogu se podvesti pod sledeću opštu shemu prikazanu u algoritmu 4.
\begin{algorithm}
\caption{Opšti algoritam relaksacije grana}
\begin{algorithmic}
\State{$\SPt{s} = 0$, $\SPt{v} = +\infty$, za sve $v\neq s$}
\While{postoji grana $(u, v)$ takva da je $\SPt{v} > \SPt{u} + d(u, v)$}
\State{$\SPt{v} = \SPt{u} + d(u, v)$}
\EndWhile
\end{algorithmic}
\end{algorithm}
Ako u grafu postoji negativan ciklus, ovaj opšti algoritam se ne zaustavlja, a ako nema negativnih ciklusa algoritam se zaustavlja i ispravno izračunava najkraća rastojanja do svih čvorova (što ćemo uskoro i dokazati). Primetimo da nije preciziran redosled obrade grana i konkretni algoritmi se razlikuju po tome kojim redom i koliko puta obrađuju grane (na primer, Dajkstrin algoritam obrađuje čvorove u redosledu neopadajućeg rastojanja i redom relaksira grane koje iz njih izlaze). Obično je redosled obrade takav da se pod određenim pretpostavkama o grafu unapred zna da je dostignuto konačno rešenje, tj. takav da se ne vrši efektivna provera da li postoje grane koje se mogu relaksirati.
Dokažimo zajednička svojstva algoritama zasnovanih na relaksaciji grana. Iako neke od narednih lema važe i u slučaju kada u grafu postoji negativni ciklus, to nam neće biti potrebno u analizi algoritama, tako da ćemo u svim narednim lemama razmatrati samo grafove bez negativnih ciklusa (osim ako je naglašeno drugačije).
Lema 2.9.1. [Nejednakost trougla] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa i neka \(x.\mathit{SP}\) označava najkraće rastojanje od čvora \(s\in V\) do čvora \(x \in V\). Za svaku granu \((u, v) \in E\) važi \(u.\mathit{SP} + d(u, v) \geq v.\mathit{SP}\).
Dokaz. Ne može da važi \(v.\mathit{SP} > u.\mathit{SP} + d(u, v)\), jer bi tada postojao put od \(s\) do \(u\) na koji bi se mogla nadovezati grana \((u, v)\), čime bi se dobio put od \(s\) do \(v\) koji bi bio kraći od najkraćeg puta od \(s\) do \(v\), što je kontradikcija. \(\Box\)
Jasno je da se relaksacijom samo može smanjiti procena rastojanja \(v.\overline{\mathit{SP}}\). Naredna lema tvrdi da ta procena nikada ne može biti manja od stvarne vrednosti najkraćeg rastojanja \(v.\mathit{SP}\).
Lema 2.9.2. [Donja granica procene rastojanja] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa i neka za svaki čvor \(v\in V\), \(v.\mathit{SP}\) označava najkraće rastojanje od čvora \(s\) do čvora \(v\), a \(v.\overline{\mathit{SP}}\) tekuću procenu tog rastojanja tokom izvršavanja postupka relaksacije grana (u proizvoljnom redosledu). Tokom čitavog tog procesa za svaki čvor \(v\) važi \(v.\overline{\mathit{SP}} \geq v.\mathit{SP}\).
Dokaz. Tvrđenje dokazujemo indukcijom po broju relaksiranih grana. Bazu indukcije čini slučaj inicijalizacije. Za sve čvorove \(v \neq s\) mora da važi \(v.\mathit{SP} \leq v.\overline{\mathit{SP}} = +\infty\). Pošto graf nema negativni ciklus koji sadrži \(s\), važi \(s.\overline{\mathit{SP}}=s.\mathit{SP} = 0\).
Pretpostavimo da tvrđenje važi nakon \(k\) relaksiranih grana i dokažimo da važi i nakon relaksiranja dodatne grane \((u, v)\). Za sve čvorove \(x \neq v\) ne menja se vrednost \(x.\overline{\mathit{SP}}\), pa na osnovu induktivne hipoteze važi \(x.\overline{\mathit{SP}} \geq x.\mathit{SP}\). Za čvor \(v\) nakon relaksacije važi \(v.\overline{\mathit{SP}} = u.\overline{\mathit{SP}} + d(u, v)\). Na osnovu induktivne hipoteze važi \(u.\overline{\mathit{SP}} \geq u.\mathit{SP}\), pa je \(v.\overline{\mathit{SP}} \geq u.\mathit{SP} + d(u, v)\), međutim, na osnovu nejednakosti trougla (leme 2.9.1) važi \(u.\mathit{SP} + d(u, v) \geq v.\mathit{SP}\), pa važi \(v.\overline{\mathit{SP}} \geq v.\mathit{SP}\). \(\Box\)
Jasno je da kada jednom procena \(v.\overline{\mathit{SP}}\) dostigne vrednost \(v.\mathit{SP}\) ona sve vreme nadalje ostaje jednaka toj vrednosti (jer relaksacija samo može smanjiti vrednost \(v.\overline{\mathit{SP}}\), a na osnovu prethodne leme znamo da ona ne može biti manja od \(v.\mathit{SP}\).
Naredna lema nam garantuje da će nakon relaksacija grana iz čvora \(u\), za koji je već izračunata vrednost najkraćeg rastojanja od početnog čvora \(s\) (tj. važi \(u.\overline{\mathit{SP}} = u.\mathit{SP}\)), biti ispravno izračunate vrednosti najkraćeg rastojanja onih njegovih suseda \(v\) za koje se najkraći put završava granom \((u,v)\).
Lema 2.9.3. [Relaksacija poslednje grane na najkraćem putu] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa i neka je \((u, v)\) poslednja grana na najkraćem putu od \(s\in V\) do \(v\in V\). Nakon što se u trenutku kada važi \(u.\overline{\mathit{SP}} = u.\mathit{SP}\) ta grana relaksira ili se ustanovi da se ne može relaksirati, važi \(v.\overline{\mathit{SP}} = v.\mathit{SP}\).
Dokaz. Pošto je \((u, v)\) poslednja grana na najkraćem putu do \(v\), važi da je \(v.\mathit{SP} = u.\mathit{SP} + d(u, v)\). Zato je \(v.\overline{\mathit{SP}} \geq v.\mathit{SP} = u.\mathit{SP} + d(u, v) = u.\overline{\mathit{SP}} + d(u, v)\). Nakon što se grane \((u, v)\) relaksira ili se ustanovi da to nije moguće, važi da je vrednost \(v.\overline{\mathit{SP}}\) minimum stare vrednosti \(v.\overline{\mathit{SP}}\) i vrednosti \(u.\overline{\mathit{SP}} + d(u, v)\). Zato važi \(v.\overline{\mathit{SP}} = u.\overline{\mathit{SP}} + d(u, v) = u.\mathit{SP} + d(u, v) = v.\mathit{SP}\). \(\Box\)
Naredna lema nam garantuje da ako ne postoji grana koja se može relaksirati, tada su sva najkraća rastojanja ispravno izračunata.
Lema 2.9.4. [Uslov za postojanje grane koja se može relaksirati] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa i neka je za neki čvor \(v\in V\) važi \(v.\overline{\mathit{SP}} \neq v.\mathit{SP}\). Tada postoji grana \(e \in E\) koja se može relaksirati.
Dokaz. Neka je \((s\equiv v_1, v_2, \ldots, v_n = v)\) najkraći put od početnog čvora do čvora \(v\) i neka je \(v_i\) prvi čvor na tom putu za koji je \(v_i.\overline{\mathit{SP}} \neq v_i.\mathit{SP}\). Pošto za čvor \(v_1 \equiv s\) sve vreme važi \(s.\overline{\mathit{SP}} = s.\mathit{SP} = 0\), mora važiti \(i > 0\). Ako se grana \((v_{i-1}, v_i)\) ne bi mogla relaksirati, na osnovu leme 2.9.3 moralo bi da važi \(v_i.\overline{\mathit{SP}} = v_i.\mathit{SP}\), što je kontradikcija. Dakle, postoji grana koja se može relaksirati. \(\Box\)
Sada je jednostavno dokazati korektnost opšte sheme relaksacije grana.
Teorema 2.9.3. [Zaustavljanje i korektnost opšteg algoritma] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa. Tada se algoritam 4 zaustavlja i nakon zaustavljanja za svaki čvor \(v \in V\) važi \(v.\overline{\mathit{SP}} = v.\mathit{SP}\).
Dokaz. Pošto se sve vrednosti \(v.\overline{\mathit{SP}}\) smanjuju tokom izvršavanja algoritma (u svakoj relaksaciji neke grane strogo se smanji vrednost \(v.\overline{\mathit{SP}}\) za neki čvor \(v\)), a na osnovu leme 2.9.2 su one ograničene odozdo, u jednom trenutku sve vrednosti \(v.\overline{\mathit{SP}}\) će dostići svoje granice \(v.\mathit{SP}\). To je sasvim jasno ako su u pitanju grane celobrojne težine, jer je zbir svih vrednosti \(v.\overline{\mathit{SP}}\) opadajući niz celih brojeva koji je odozdo ograničen zbirom svih vrednosti \(v.\mathit{SP}\), pa mora biti konačan. Ako su grane racionalni brojevi, mogao ni da postoji beskonačno dugačak opadajući niz racionalnih brojeva koji je odozdo ograničen. Međutim, množenjem svih težina nekim pogodno odabranim stepenom broja 10 može se lako postići da težine svih grana postanu celobrojne, bez suštinske izmene problema, tako da je i u tom slučaju jasno da se algoritam mora zaustaviti nakon konačnog broja koraka.
Ako bi se tada mogla relaksirati neka grana \((u, v)\), važilo bi da je \(v.\overline{\mathit{SP}} > u.\overline{\mathit{SP}} + d(u, v)\), tj. \(v.\mathit{SP} > u.\mathit{SP} + d(u, v)\), što je nemoguće na osnovu nejednakosti trougla (lema 2.9.1). Dakle, tada nema grana koje se mogu relaksirati, pa se algoritam zaustavlja.
Pošto se algoritam zaustavi, ne postoji grana koja se može relaksirati. Ako bi za neki čvor \(v\in V\) važilo \(v.\overline{\mathit{SP}} \neq v.\mathit{SP}\), na osnovu leme 2.9.4 postojala bi grana koja bi se mogla relaksirati, što je kontradikcija. \(\Box\)
Ukoliko graf ima negativne težine grana, ali ne sadrži ciklus negativne težine, najkraći putevi iz datog čvora \(s\) mogu se odrediti Belman-Fordovim algoritmom1. Važi i više od toga: ako u grafu postoji ciklus negativne težine, Belman-Fordov algoritam to detektuje.
U izvođenju ovog algoritma biće nam značajna naredna lema, koja garantuje da će nakon što se redom relaksira jedna po jedna grana najkraćeg puta do nekog čvora uspešno biti izračunato najkraće rastojanje do tog čvora (kao i do svih ostalih čvorova na tom putu).
Lema 2.9.5. [Relaksacija najkraćeg puta] Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa i neka je \(p=(s\equiv v_1, \ldots, v_j)\) najkraći put od \(s\) do \(v_j\). Proizvoljni niz relaksacija grana koji uključuje i redom relaksacije grana \((v_1, v_2)\), \((v_2, v_3)\), \(\ldots\), \((v_{j-1}, v_j)\) dovodi do toga da važi \(v_j.\overline{\mathit{SP}} = v_j.\mathit{SP}\). Pre, posle i između ovih relaksacija je dopušteno vršiti bilo koje druge relaksacije grana.
Dokaz. Tvrđenje dokazujemo indukcijom po čvorovima u nizu \(p\) tj. dokazujemo da za svako \(1 \leq k \leq j\) nakon relaksacija grana \((v_1, v_2)\), \((v_2, v_3)\), \(\ldots\), \((v_{k-1}, v_k)\) važi \(v_k.\overline{\mathit{SP}} = v_k.\mathit{SP}\).
Baza indukcije je čvor \(s\). Pošto graf nema negativnih ciklusa, važi \(s.\mathit{SP} = 0\). Vrednost \(s.\overline{\mathit{SP}}\) mora sve vreme biti 0, jer je, znamo na osnovu leme 2.9.2, uvek veća ili jednaka od \(s.\mathit{SP}\), tokom relaksacije se samo može smanjiti, a inicijalizuje se na 0.
Pretpostavimo da smo redom relaksirali grane \((v_1, v_2)\), \((v_2, v_3)\), \(\ldots\), \((v_{k-2}, v_{k-1})\) i da je \(v_{k-1}.\overline{\mathit{SP}} = v_{k-1}.\mathit{SP}\). U nekom trenutku nakon toga se pokušava relaksacija grane \((v_{k-1}, v_k)\). Na osnovu leme 2.9.3 sledi da nakon toga sigurno važi \(v_k.\overline{\mathit{SP}} = v_k.\mathit{SP}\). Na osnovu leme 2.9.2 važi \(v_k.\overline{\mathit{SP}} \geq v_k.\mathit{SP}\), pa se ova vrednost ne može dalje smanjivati i neće se menjati. \(\Box\)
Dakle, dovoljno je da naš algoritam obezbedi da se sve grane svih najkraćih puteva relaksiraju redom od prve do poslednje. Belman-Fordov algoritam to postiže tako što ukupno \(|V|-1\) puta proizvoljnim redosledom izvršava relaksaciju svih grana u grafu.
\begin{algorithm}
\caption{Belman-Fordov algoritam}
\begin{algorithmic}
\State{$\SPt{s} = 0$, $\SPt{v} = +\infty$, za sve $v\neq s$}
\For{$i = 1..|V|-1$}
\ForAll{$(u, v) \in E$}
\If{$\SPt{v} > \SPt{u} + d(u, v)$}
\State{$\SPt{v} = \SPt{u} + d(u, v)$}
\EndIf
\EndFor
\EndFor
\end{algorithmic}
\end{algorithm}
Tvrdimo da su, ako graf ne sadrži negativan ciklus, nakon toga korektno izračunati najkraći putevi od čvora \(v\) do svih čvorova u grafu. Za čvorove koji su nedostižni iz početnog čvora, dužina najkraćeg puta ostaje \(+\infty\). Ako graf sadrži negativan ciklus, nakon svih ovih relaksacija i dalje postoje grane koje se mogu relaksirati (provera postojanja takve grane je ujedno i način da se proveri da li postoji negativan ciklus, tj. da li su pronađena rastojanja korektna).
Dokažimo ovo tvrđenje.
Lema 2.9.6. Neka je dat težinski graf \(G = (V, E)\) bez negativnih ciklusa. Kada se Belman-Fordov algoritam (algoritam 5) primeni na graf \(G\), za svaki čvor \(v\) važi \(v.\overline{\mathit{SP}} = v.\mathit{SP}\).
Dokaz.
Ako je \(v\) dostižan iz \(s\) u grafu bez negativnih ciklusa mora da postoji prost put od \(s\) do \(v\). U tom putu ne može da bude više od \(|V|\) čvorova, pa ni više od \(|V| - 1\) grana. Pošto se u svakoj iteraciji relaksiraju sve grane, u prvoj iteraciji je sigurno relaksirana prva grana na tom putu, u drugoj druga itd. (naravno moguće je da se u nekoj iteraciji redom relaksira i više grana najkraćeg puta). Pošto se vrši \(|V|-1\) iteracija, sve grane su redom relaksirane, pa na osnovu leme 2.9.5 važi \(v.\overline{\mathit{SP}} = v.\mathit{SP}\).
Ako \(v\) nije dostižan iz \(s\) tada je \(v.\overline{\mathit{SP}} = v.\mathit{SP} = +\infty\). Zaista, vrednost \(v.\overline{\mathit{SP}}\) se inicijalizuje na \(+\infty\), a ne može da se smanji ispod stvarne vrednosti \(v.\mathit{SP}\) koja je jednaka \(+\infty\). \(\Box\)
Teorema 2.9.4. [Zaustavljanje i korektnost Belman-Fordovog algoritma] Ako u grafu nema ciklusa negativne težine, Belman-Fordov algoritam se zaustavlja i za sve čvorove \(v\) grafa važi \(v.\overline{\mathit{SP}} = v.\mathit{SP}\) i nijedna grana se ne može relaksirati. Ako u grafu postoji ciklus negativne težine, po završetku algoritma postoji bar jedna grana koja se može relaksirati.
Dokaz. Prvi deo tvrđenja direktno sledi iz leme 2.9.6. Za svaku granu \((u, v)\) na osnovu nejednakosti trougla važi \(v.\overline{\mathit{SP}} = v.\mathit{SP} \leq u.\mathit{SP} + d(u, v) = u.\overline{\mathit{SP}} + d(u, v)\), pa se grana \((u, v)\) ne može relaksirati.
Pretpostavimo da \(G\) sadrži ciklus negativne težine \(c=(v_0,v_1,\ldots,v_k), v_k=v_0\), dostižan iz čvora \(s\) (slika 9).
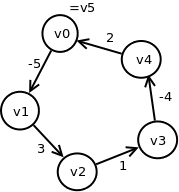
Tada je:
\[\sum_{i=1}^k d(v_{i-1},v_i)<0\](2)
Pretpostavimo suprotno, da se nijedna grana ne može relaksirati, tj. da za svaku granu \((u,v)\in E\) važi \(v.\overline{\mathit{SP}}\le u.\overline{\mathit{SP}}+d(u,v)\). Tada i za svaku granu ciklusa \((v_{i-1},v_i)\in E, i=1,\ldots,k\), važi: \(v_i.\overline{\mathit{SP}}\le v_{i-1}.\overline{\mathit{SP}}+d(v_{i-1},v_i).\) Sabiranjem ovih nejednakosti za sve grane ciklusa dobija se:
\[\sum_{i=1}^k v_i.\overline{\mathit{SP}} \le \sum_{i=1}^k v_{i-1}.\overline{\mathit{SP}}+\sum_{i=1}^k d(v_{i-1},v_i)\]
Pošto je \(v_0=v_k\), važi:
\[\sum_{i=1}^k v_i.\overline{\mathit{SP}} = \sum_{i=1}^k v_{i-1}.\overline{\mathit{SP}}\]
te dalje važi:
\[\sum_{i=1}^k d(v_{i-1},v_i)\ge 0\]
suprotno pretpostavci (2). \(\Box\)
Primetimo da se relaksacija grana ne mora vršiti istim redosledom u svakoj od iteracija – samo je bitno da se u svakoj iteraciji relaksiraju sve grane grafa. Time se postiže da se na svakom najkraćem putu sigurno relaksira po jedna dodatna grana.
U narednom apletu možete videti kako funkcioniše Belman-Fordov algoritam i koliko redosled obrade grana može uticati na brzinu izračunavanja najkraćih iteracija.
Primetimo da se nakon izvršavanja \(i\)-te iteracije petlje, pronalaze najkraći putevi čiji broj grana ne prevazilazi vrednost \(i\).
S obzirom da se često može desiti da se najkraća rastojanja izračunaju i pre sprovođenja svih iteracija, algoritam je moguće prekinuti ranije ako se desi da se u nekoj iteraciji ne uspe relaksacija nijedne grane.
Implementacija ovog algoritma je veoma jednostavna.
// funkcija koja koriscenjem Belman-Fordovog algoritma
// racuna najkrace puteve do svih cvorova
void najkraciPuteviBelmanFord(int start) {
int brojCvorova = listaSuseda.size();
// duzina trenutno poznatog najkraceg puta do cvora
vector<Tezina> minRastojanja(brojCvorova, INF);
// prethodnik cvora na najkracem putu
vector<Cvor> roditelji(brojCvorova, -1);
// postavljamo rastojanje do polaznog cvora
minRastojanja[start] = 0;
// |V|-1 put prolazimo kroz skup svih grana
for (int k = 0; k < brojCvorova - 1; k++) {
bool biloRelaksacija = false;
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
for (const auto& [sused, tezina] : listaSuseda[cvor]) {
// ukoliko je potrebno vrsimo relaksaciju grane
if (minRastojanja[cvor] + tezina < minRastojanja[sused]) {
minRastojanja[sused] = minRastojanja[cvor] + tezina;
// i postavljamo koji cvor mu prethodi na najkracem putu
roditelji[sused] = cvor;
biloRelaksacija = true;
}
}
if (!biloRelaksacija) break;
}
// ukoliko i dalje postoji put koji je moguce skratiti
// onda graf sadrzi ciklus negativne duzine
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
for (const auto& [sused, tezina] : listaSuseda[cvor])
if (minRastojanja[cvor] + tezina < minRastojanja[sused]) {
cout << "Graf sadrzi ciklus negativne duzine" << endl;
return;
}
// stampamo najkrace puteve do svih cvorova u grafu
for (Cvor cvor = 0; cvor < brojCvorova; cvor++)
odstampajNajkraciPut(cvor, roditelji, minRastojanja);
}Složenost Belman-Fordovog algoritma iznosi \(O(|V|\cdot|E|)\), jer spoljašnjom for petljom prolazimo \(O(|V|)\) puta, a u svakoj iteraciji ove petlje prolazimo skupom svih grana u grafu.
Primer 2.9.7. Na slici 10 ilustrovano je izvršavanje Belman-Fordovog algoritma.
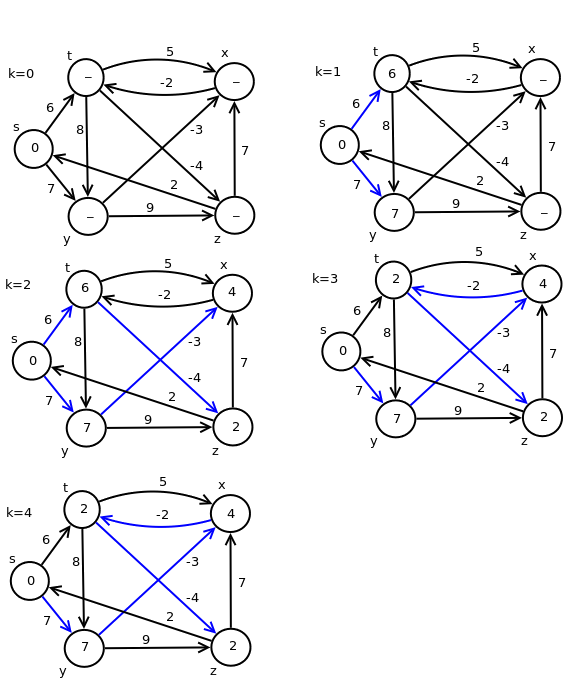
Belman-Fordov algoritam se može unaprediti tako što se smanji broj relaksacija koje se razmatraju u svakoj iteraciji algoritma. Naime, ako se trenutno najkraće rastojanje do čvora \(v\) nije izmenilo od trenutka kada su poslednji put relaksirane grane koje polaze iz čvora \(v\), onda nema potrebe ponovo vršiti relaksaciju grana koje polaze iz čvora \(v\). Na ovaj način se broj grana koje treba relaksirati u svakoj iteraciji potencijalno smanjuje. Ovaj algoritam poznat je pod nazivom brži algoritam najkraćeg puta (engl. Shortest Path Faster Algorithm – SPFA). Algoritam se može implementirati tako što se održava red u kome se čuvaju čvorovi iz kojih polaze grane koje treba relaksirati. U početku se samo početni čvor stavlja u red. Kada se čvor izvadi iz reda, pokušava se relaksacija svih grana koje iz njega polaze i ako se neka grana relaksira, njen krajnji čvor se dodaje u red (ako se već ne nalazi u njemu).
\begin{algorithm}
\caption{Algoritam SPFA}
\begin{algorithmic}
\State{$\SPt{s} = 0$, $\SPt{v} = +\infty$, za sve $v\neq s$}
\State{$Q$.push($s$)}
\While{$Q$ not empty}
\State{$u$ = $Q$.pop()}
\ForAll{$(u, v) \in E$}
\If{$\SPt{v} > \SPt{u} + d(u, v)$}
\State{$\SPt{v} = \SPt{u} + d(u, v)$}
\If{$v$ is not in $Q$}
\State{$Q$.push($v$)}
\EndIf
\EndIf
\EndFor
\EndWhile
\end{algorithmic}
\end{algorithm}
Korektnost se zasniva na činjenici da se na svakom ulazu u petlju while u redu nalaze svi čvorovi iz kojih je moguća relaksacija grana (što se može dokazati indukcijom). Ako se red isprazni relaksacije nisu moguće i sva najkraća rastojanja su ispravno određena. Ako u grafu postoji ciklus negativne težine, relaksacije su uvek moguće i algoritam se ne zaustavlja.
Zadaci:
Ričard Belman i Lester Ford su objavili ovaj algoritam 1958. i 1959. godine, međutim, smatra se da je do njega prvi došao Alfonso Simbel 1955. godine.↩︎