Uobičajena su dva načina predstavljanja grafova: matricom povezanosti i listama povezanosti.
Graf se može predstaviti matricom povezanosti, odnosno matricom susedstva grafa (engl. adjacency matrix). Neka je \(|V|=n\) i \(V=\{v_0,v_1,\ldots,v_{n-1}\}\). Matrica povezanosti grafa \(G\) je kvadratna matrica \(A=(a_{ij})\) reda \(n\), sa elementima \(a_{ij}\) koji su jednaki \(1\) (tj. \(\top\)) ako i samo ako \((v_i,v_j)\in E\), odnosno ako postoji grana od čvora \(v_i\) do čvora \(v_j\); ostali elementi matrice \(A\) imaju vrednost \(0\) (tj. \(\bot\)). Vrsta \(i\) ove matrice je, dakle, niz dužine \(n\) čija je \(j\)-ta koordinata jednaka \(1\) ako iz čvora \(v_i\) vodi grana ka čvoru \(v_j\), odnosno \(0\) u protivnom.
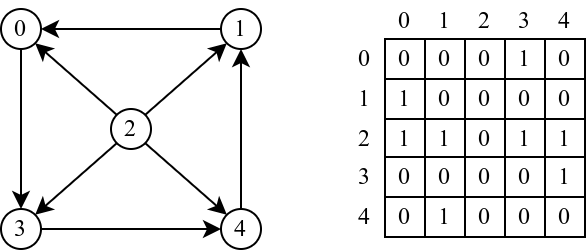
Primer 2.2.1. Primer reprezentacije jednog usmerenog grafa matricom povezanosti je prikazan na slici 1. Čvorovi su numerisani brojevima od \(0\) do \(4\). Na primer, na poziciji \((1,0)\) u matrici povezanosti nalazi se vrednost \(1\) jer postoji grana iz čvora \(1\) ka čvoru \(0\), dok se na poziciji \((0,1)\) nalazi \(0\) jer u grafu ne postoji suprotno usmerena grana.

Ako je graf neusmeren, matrica \(A\) je simetrična. Nedostatak predstavljanja grafa matricom povezanosti je to što ona uvek zauzima prostor veličine \(n^2\) tj. \(\Theta(|V|^2)\), nezavisno od toga koliko grana ima graf. Ako je broj grana u grafu mali, većina elemenata matrice povezanosti je jednaka nula.
Ako se za predstavljanje grafa koristi matrica povezanosti, složenost operacije dodavanja grane u graf, odnosno operacije uklanjanja grane iz grafa je \(O(1)\). Takođe, i ispitivanje da li su dva čvora u grafu povezana granom je složenosti \(O(1)\). Prolazak kroz sve čvorove susedne datom čvoru je složenosti \(\Theta(|V|)\).
U jeziku C++ graf predstavljen matricom povezanosti možemo deklarisati na sledeći način:
bool matricaPov[MAX][MAX];gde je MAX maksimalni broj čvorova grafa. Ako broj čvorova saznajemo tek u vreme izvršavanja programa, možemo upotrebiti dinamičke strukture podataka (na primer, vector) i upotrebiti sledeću reprezentaciju:
vector<vector<bool>> matricaPov(n);
for (int i = 0; i < n; i++)
matricaPov[i].resize(n);Umesto da se i sve nepostojeće grane eksplicitno predstavljaju, kao što je slučaj sa matricom povezanosti grafa, mogu se formirati povezane liste od jedinica iz \(i\)-te vrste, \(i=0,1,\ldots,n-1\). Ovaj način predstavljanja grafa naziva se liste povezanosti, odnosno liste susedstva (engl. adjacency list). Svakom čvoru pridružuje se povezana lista koja sadrži sve čvorove do kojih postoji grana iz tog čvora. Lista može biti uređena prema rednim brojevima čvorova na krajevima njenih grana. Graf je predstavljen nizom lista. Svaki element niza sadrži ime (indeks) čvora i pokazivač na njegovu listu suseda.
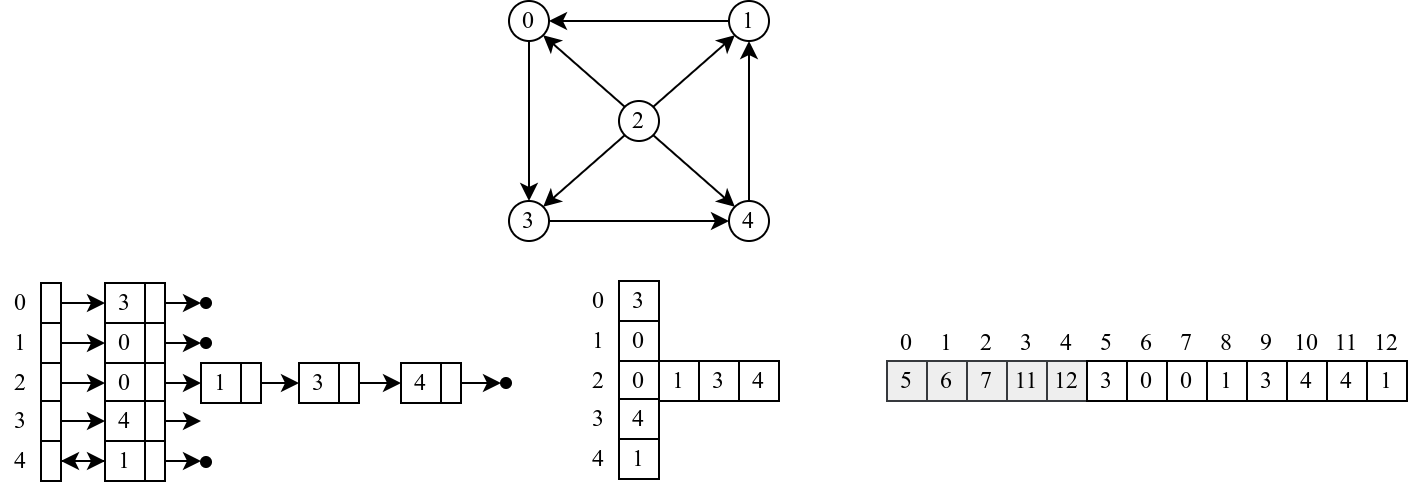
Primer 2.2.2. Primer predstavljanja grafa listama povezanosti je prikazan na slici 2. Lista povezanosti pridružena čvoru \(1\) je dužine \(1\) jer iz čvora \(1\) polazi tačno jedna grana. Slično, lista povezanosti pridružena čvoru \(2\) je dužine \(4\) jer iz čvora \(2\) polaze četiri grane.
Iako naziv tako sugeriše, implementacija ovakve reprezentacije grafa ne mora biti zasnovana na povezanim listama, već se umesto povezanih listi može koristiti dinamički proširiv niz (vektor), ili neka reprezentacija skupa (balansirano binarno drvo ili heš tabela).
U jeziku C++ se graf predstavljen listama povezanosti, pri čemu se liste povezanosti implementiraju korišćenjem vektora, deklariše na sledeći način:
vector<vector<int>> listaSuseda(n);Na primer, usmereni graf sa slike 2 predstavićemo kao:
vector<vector<int>> listaSuseda {{3}, {0}, {0, 1, 3, 4}, {4}, {1}};Broj čvorova grafa možemo dobiti kao broj elemenata u spoljašnjem vektoru:
int brCvorova = listaSuseda.size();Novu granu (cvorOd,cvorDo) možemo dodati u graf na sledeći način:
listaSuseda[cvorOd].push_back(cvorDo);dok kroz sve susede čvora možemo iterirati na sledeći način:
for (int cvorDo : listaSuseda[cvorOd])
...Ako je graf statički, odnosno ako nisu dozvoljena umetanja i brisanja čvorova i grana, onda se liste povezanosti mogu predstaviti statičkim nizom \(a\) dužine \(|V|+|E|\) u slučaju usmerenog grafa (odnosno dužine \(|V|+2|E|\) u slučaju neusmerenog grafa). Prvih \(|V|\) članova niza su pridruženi čvorovima. Element niza \(a\) na poziciji \(i\), \(i<|V|\) je pridružen čvoru \(v_i\) i sadrži indeks početka spiska čvorova susednih čvoru \(v_i\), \(i=0,1,\ldots,n-1\), dok se na pozicijama \(i\), \(|V|\le i < |V|+|E|\) nalaze informacije o susedima čvorova. Naime, susedi čvora \(v_i\) za \(0\le i < n-1\) nalaze se u nizu \(a\) na pozicijama \([a[i],a[i+1])\), dok se susedi čvora \(v_{n-1}\) nalaze na pozicijama od \(a[n-1]\) do kraja niza (slika 2, desno). Primetimo da se na poziciji \(0\) u nizu \(a\) nalazi vrednost koja odgovara broju čvorova u grafu.
Primer 2.2.3. Primer predstavljanja grafa sa slike 2(a) statičkim nizom je prikazan na slici 2, desno. Na poziciji \(0\) nalazi se vrednost \(5\), a na poziciji \(1\) vrednost \(6\), što ukazuje na to da se na pozicijama \([5,6)\) u ovom nizu nalaze susedi čvora \(0\) – u ovom slučaju to je samo čvor \(3\). Susedi čvora \(2\) nalaze se na pozicijama \([7,11)\) i to su redom \(0,1,3\) i \(4\).
Sa matricama povezanosti je jednostavnije raditi. S druge strane, liste povezanosti su prostorno efikasnije za grafove sa malim brojem grana: njihova memorijska složenost je \(O(|V|+|E|)\), za razliku od matrica povezanosti čija je memorijska složenost \(O(|V|^2)\). U praksi se često radi sa retkim grafovima koji imaju znatno manje grana od maksimalnog mogućeg broja, što je \(n(n-1)/2\) za neusmereni, odnosno \(n(n-1)\) za usmereni graf ako isključimo petlje (odnosno \(n(n-1)/2+n=n(n+1)/2\) grana za neusmereni, odnosno \(n(n-1)+n=n^2\) za usmereni graf ako dozvolimo petlje) i tada je efikasnije koristiti liste povezanosti. U slučaju kada se za implementaciju koriste povezane liste, ispitivanje da li su dva čvora u grafu povezana, kao i uklanjanje grane iz grafa je u najgorem slučaju složenosti \(O(|V|)\). U slučaju kada se za implementaciju lista povezanosti koriste heš tabele, očekivano vreme izvršavanja ovih operacija je \(O(1)\). Prolazak kroz sve čvorove susedne čvoru \(v\) je složenosti \(O(d(v))\), gde je \(d(v)\) stepen čvora \(v\) u slučaju neusmerenog grafa, odnosno izlazni stepen čvora \(v\) ako je graf usmeren. Dodavanje novog čvora u graf je jednostavnije nego u slučaju reprezentacije grafa matricom povezanosti.
Treba pomenuti da postoje i drugi načini za predstavljanje grafa: graf se, na primer, može čuvati i kao niz grana, gde se za svaku granu čuva informacija sa kojim čvorovima je incidentna.
U narednim algoritmima smatraćemo da je graf sa kojim radimo dinamički i da je, ako nije drugačije navedeno, zadat listama povezanosti.