Formalno, graf \(G=(V,E)\) se sastoji od skupa \(V\) čvorova i skupa \(E\) grana (oznake \(V\) i \(E\) su početna slova engleskih reči za teme – vertex i granu – edge). Grana najčešće odgovara paru različitih čvorova, mada su ponekad dozvoljene i petlje, odnosno grane koje vode od čvora ka njemu samom. Graf može biti neusmeren tj.
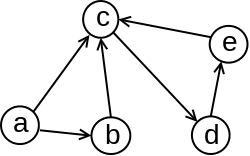
neorijentisan ili usmeren tj. orijentisan. Grane usmerenog grafa su uređeni parovi čvorova i kod njih je redosled čvorova koje grana povezuje bitan. Ako se graf predstavlja grafički, onda se grane usmerenog grafa crtaju kao strelice usmerene od jednog čvora – početka ka drugom čvoru – kraju grane (slika 1). Grane neusmerenog grafa su neuređeni parovi čvorova: one se crtaju kao obične linije, bez usmerenja (slika 2).

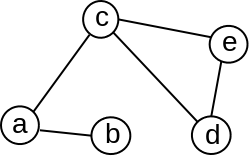
Susedom čvora \(u\) nazvaćemo svaki čvor \(v\) do kog postoji grana iz čvora \(u\).
Primer 2.1.1. Susedi čvora \(c\) u neusmerenom grafu sa slike 2 su čvorovi \(a\), \(d\) i \(e\), dok je u usmerenom grafu sa slike 1 jedini sused čvora \(c\) čvor \(d\). Primetimo da je u grafu prikazanom na slici 1 čvor \(c\) povezan i sa čvorovima \(a\), \(b\) i \(e\), međutim, oni nisu susedi čvora \(c\) jer su odgovarajuće grane usmerene od čvorova \(a,b\) i \(e\) ka čvoru \(c\).
Stepen \(d(v)\) čvora \(v\) u neusmerenom grafu je broj grana susednih čvoru \(v\) (odnosno broj grana koje čvor \(v\) povezuju sa nekim drugim čvorom). U usmerenom grafu razlikujemo ulazni stepen čvora \(v\), koji je jednak broju grana za koje je čvor \(v\) kraj, i izlazni stepen čvora \(v\), koji je jednak broju grana za koje je čvor \(v\) početak.
Primer 2.1.2. Stepen čvora \(c\) u neusmerenom grafu sa slike 2 je \(3\), dok je ulazni stepen čvora \(c\) usmerenog grafa sa slike 1 jednak \(3\), a izlazni stepen \(1\).
U narednom apletu možete proveriti svoje razumevanje stepena čvora grafa.
Put od čvora \(v_1\) do čvora \(v_k\) u grafu \(G\) je niz čvorova grafa \((v_1,v_2,\ldots,v_k)\) povezanih granama grafa \((v_1,v_2)\), \((v_2,v_3)\), \(\ldots\), \((v_{k-1},v_k)\). Put je prost ako se svaki čvor u njemu pojavljuje samo jednom. Za čvor \(v\) se kaže da je dostižan iz čvora \(u\) ako postoji put (usmeren, odnosno neusmeren, zavisno od grafa) od čvora \(u\) do čvora \(v\). Po definiciji svaki čvor \(v\) je dostižan iz čvora \(v\) tj. iz sebe. Ciklus je put čiji se prvi i poslednji čvor poklapaju. Ciklus je prost ako se, sem prvog i poslednjeg čvora, ni jedan drugi čvor u njemu ne javlja dva puta.
Primer 2.1.3. Niz čvorova \((a,b,c,d,e)\) u usmerenom grafu sa slike 1 predstavlja jedan prost put u tom grafu, dok put \((b,c,d,e,c)\) nije prost.
Čvor \(e\) grafa sa slike 1 dostižan je iz čvora \(a\) jer postoji put \((a,c,d,e)\) od čvora \(a\) do čvora \(e\).
Niz čvorova \((c,d,e,c)\) predstavlja prost ciklus i u datom usmerenom i u datom neusmerenom grafu.
Usmeren graf u kome nema ciklusa naziva se usmeren aciklički graf (engl. directed acyclic graph, DAG). Neusmereni oblik usmerenog grafa \(G=(V,E)\) je isti graf, bez smerova na granama (tako da su parovi čvorova u \(E\) neuređeni). Za neusmeren graf se kaže da je povezan ako postoji put između proizvoljna dva čvora u grafu. Za usmerene grafove razlikujemo pojam slabe i jake povezanosti: usmereni graf je slabo povezan ako u njegovom neusmerenom obliku postoji put između svaka dva čvora u grafu, a jako povezan ako za svaka dva čvora \(u\) i \(v\) u grafu postoji usmeren put od čvora \(u\) do čvora \(v\) i usmeren put od čvora \(v\) do čvora \(u\).
Primer 2.1.4. Neusmeren graf sa slike 2 je povezan.
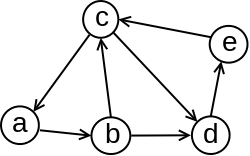
Usmeren graf sa slike 1 je slabo povezan, ali nije jako povezan: od čvora \(b\), na primer, nije moguće stići do čvora \(a\). S druge strane, graf sa slike 3 je jako povezan.
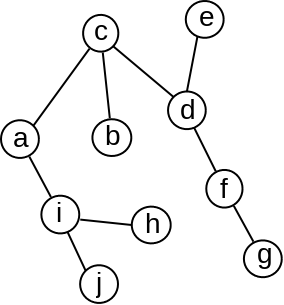
Neusmereni graf je šuma ako ne sadrži cikluse (slika 4). Drvo je povezana šuma (slika 5). Šuma sadrži jedno ili više drveta.
Graf \(G'=(V', E')\), \(E' \subseteq V' \times V'\), je podgraf grafa \(G=(V, E), E \subseteq V \times V\) ako istovremeno važi \(V'\subseteq V\) i \(E'\subseteq E\). Na primer, graf sa skupom čvorova \(\{a,b,c,d\}\) i skupom grana \(\{(a,b),(a,c),(c,d)\}\) je jedan podgraf usmerenog grafa sa slike 1. Povezujuće drvo neusmerenog grafa \(G\) je njegov podgraf koji je drvo i sadrži sve čvorove grafa \(G\). Povezujuća šuma neusmerenog grafa \(G\) je njegov podgraf koji je šuma i sadrži sve čvorove grafa \(G\).
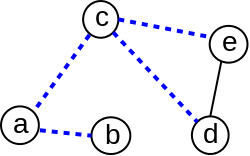
Primer 2.1.5. Grane jednog povezujućeg drveta neusmerenog grafa sa slike 2 su prikazane plavom bojom na slici 6: ono sadrži sve čvorove grafa i skup grana \(\{(a,b),(a,c),(c,d),(c,e)\}\).
Ako neusmereni graf \(G=(V,E)\) nije povezan, onda se on može na jedinstven način razložiti u skup povezanih podgrafova, čiji skupovi čvorova predstavljaju klase ekvivalencije za relaciju dostižnosti i koji se nazivaju komponente povezanosti grafa \(G\).
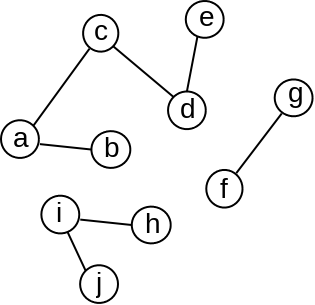
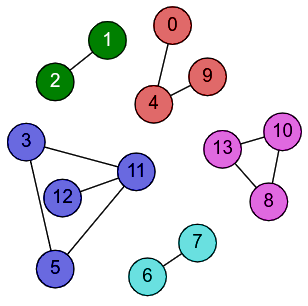
Primer 2.1.6. Na slici 7 prikazan je graf sa \(5\) komponenata povezanosti (čvorovi svake komponente su prikazani zasebnom bojom).
U narednom apletu možete proveriti svoje razumevanje pojma komponenata povezanosti grafa.