7.
Ako su kod jednakostranog petougla tri ugla, bila uzastopna ili ne, jednaka među sobom, petougao je jednakougli.
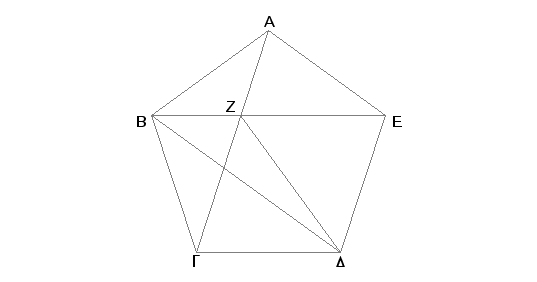
Neka su, prvo, tri uzastopna ugla, A, B, G jednakostranog petougla ABGDE jednaka među sobom. Tvrdim da su svi uglovi petougla ABGDE jednaki među sobom.
Zaista, nacrtajmo spojnice AG, BE, ZD. Pošto su dve strane GB i BA jednake dvema stranama BA i AE, svaka svakoj, i ugao GBA jednak uglu BAE, biće i osnovica AG jednaka osnovici BE, trougao ABG jednak trouglu ABE, i preostali uglovi jednaki preostalim uglovim, koji su spram jednakih strana [I.4], naime ugao BGA uglu BEA, i ugao ABE uglu GAB, pa će stoga i strana AZ biti jednaka strani BZ [I.6]. A dokazano je da je i celo AG jednako celom BE. Dakle, i ostatak ZG jednak je ostatku ZE. A i GD je jednako DE. Dve strane ZG i GD jednake su dvema stranama ZE i ED, a osnovica ZD je zajednička. Prema tome je ugao ZGD jednak uglu ZED [I.8]. A dokazano je da je i ugao BGA jednak uglu AEB. Prema tome je i ceo ugao BGD jednak celom uglu AED. Ali po pretpostavci ugao BGD jednak je uglovima kod A i B, pa je prema tome i ugao AED jednak uglovima kod A i B. Slično se dokazuje da je i ugao GDE jednak uglovima kod A, B, G. Na ovaj način petougao ABGD je jednakougli.
Neka su sad jednaki ne tri uzastopna ugla, već uglovi kod tačaka A, G, D. Tvrdim da je i tada petougao ABGDE jednakougli.
Zaista, nacrtajmo BD. Pošto su dve strane BA i AE jednake dvema stranama BG i GD i obuhvataju jednake uglove, biće osnovica BE jednaka osnovici BD, trougao ABE jednak trouglu BGD, i ostali uglovi jednaki ostalim uglovima, koji su spram jednakih strana [I.4]. Prema tome je ugao AEB jednak uglu GDB. A i ugao BED jednak je uglu BDE, pošto je strana BE jednaka strani BD [I.5]. Na taj nčin je i ceo ugao AED jednak celom uglu GDE. Ali ugao GDE, po pretpostavci, jednak je uglovima kod A i kod G, pa je prema tome i ugao AED jednak uglovima kod A i kod G. Iz istih razloga i ugao ABG jednak je uglovima kod A, G i D.
Na ovaj način petougao ABGDE je jednakougli. A to je trebalo dokazati.