4.
Ako je duž podeljena neprekidno, biće zbir kvadrata na celoj duži i na manjem delu jednak trostrukom kvadratu na većem delu.
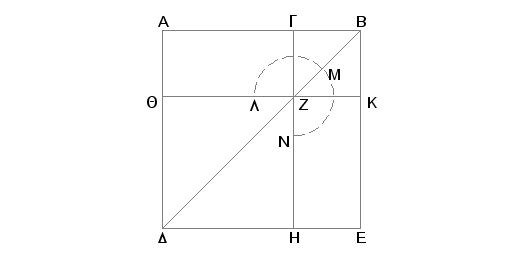
Neka je duž AB podeljena tačkom G neprekidno i neka je AG veći deo. Tvrdim da je zbir kvadrata na AB i na BG triput veći od kvadrata na GA.
Zaista, konstruišimo na AB kvadrat ADEB i nacrtajmo sliku. Pošto je sad AB tačkom G podeljeno neprekidno i veći deo je AG, biće pravougaonik obuhvaćen od AB i BG jednak kvadratu na AG [VI, Def. 3, VI.17]. I pošto je AK pravougaonik obuhvaćen od AB i BG, a kvadrat na AG je QH, biće AK jednako QH. I pošto je AZ jednako ZE, dodajmo im isto GK. Tada je celo AK jednako celom GE, pa je prema tome zbir AK i GE dvostruko AK. Ali zbir AK i GE je zbir gnomona LMN i kvadrata GK. Prema tome je zbir gnomona LMN i kvadrata GK dvostruko AK. Ali već je dokazano da je AK jednako i QH. Prema tome, gnomon LMN i [kvadrat GK su dvaput veći od kvadrata QH i znači gnomon LMN i] kvadrati GK i QH triput su veći od kvadrata QH. No gnomon LMN i kvadrat GK i QH čine ceo kvadrat AE i kvadrat GK, a to su kvadrati na AB i na BG, dok je HQ kvadrat na AG.
Na ovaj način je zbir kvadrata na AB i na BG jednak trostrukom kvadratu na AG. A to je trebalo dokazati.