2.
Ako je kvadrat na nekoj duži pet puta veći od kvadrata na jednom njenom delu i udvostručeni taj deo podeljen neprekidno, biće preostali deo polazne duži veći deo.
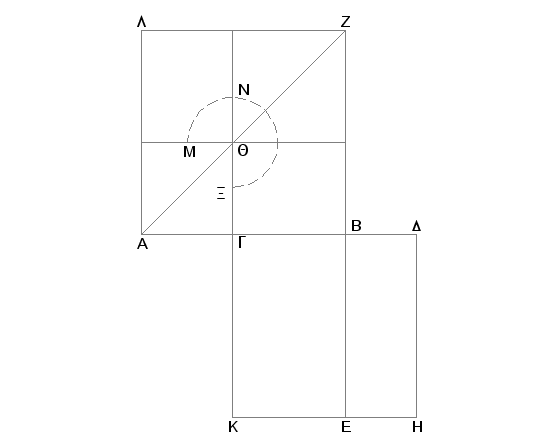
Neka je kvadrat na duži AB pet puta veći od kvadrata na AG i neka je udvostručeno AG duž GD. Tvrdim da je GB veći deo duži GD podeljene neprekidno.
Zaista, konstruišimo na svakoj od duži AB i GD kvadrate AZ i GH, u AZ nacrtajmo uobičajenu sliku i produžimo BE. Pošto je kvadrat na BA pet puta veći od kvadrata na AG, biće AZ petostruko AQ. Prema tome je gnomon MNX četvorostruko AQ. I pošto je DG dvostruko GA, biće kvadrat na DG četvorostruki kvadrat na GA, tj. GH od AQ. A dokazano je da je i gnomon MNX četvorostruko AQ. Prema tome je gnomon MNX jednak GH. I pošto je DG dvostruko GA, DG je jednako GK, a AG jednako GQ (pa prema tome, i KG je udvostručeno GQ), biće i KB dvostruko BQ [VI.1]. Takođe je i zbir LQ i QB jednak dvostrukom QB. Prema tome je KB jednako zbiru LQ i QB. A dokazano je da je i ceo gnomon MNX jednak celom GH, te je i ostatak QZ jednak BH. No pravougaonik BH je obuhvaćen dužima GD i DB, jer je GD jednako DH, a QZ je kvadrat na GB. Prema tome je pravougaonik obuhvaćen od GD i DB jednak kvadratu na GB. Na taj način je DG prema GB kao GB prema BD. Međutim DG je veće od GB, a prema tome i GB je veće od BD. Dakle GB je veći deo duži GD podeljene neprekidno.
Na ovaj način, ako je kvadrat na nekoj duži pet puta veći od kvadrata na jednom njenom delu i udvostručeni taj deo je podeljen neprekidno, biće preostali deo polazne duži veći deo. A to je trebalo dokazati.