14.
Konstruisati oktaedar, obuhvatiti ga sferom, kao u predhodnom slučaju, i dokazati da je kvadrat na prečniku sfere dvaput veći od kvadrata na ivici oktaedra.
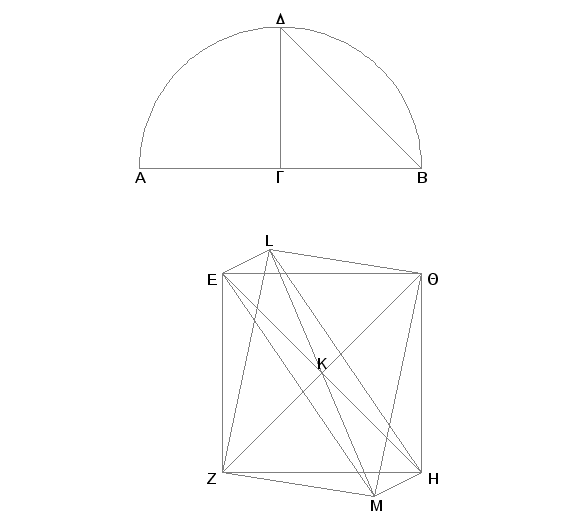
Odmerimo prečnik date sfere AB, prepolovimo ga tačkom G i nacrtajmo na AB polukrug ADG. Zatim iz tačke G povucimo pravu normalnu na AB; povucimo DB i uzmimo kvadrat EZHQ čije su sve strane jednake DB. Dalje, povucimo QZ, EH, pa iz tačke K povucimo, pod pravim uglovima prema ravni kvadrata EZHQ, pravu KL, produžimo je sa druge strane ravni kao KM. Na svakoj od KL i KM odmerimo prave KL, KM jednake jednoj od EK, ZK, HK, QK i nacrtajmo LE, LZ, LH, LQ, ME, MZ, MH, MQ. Pošto je KE jednako KQ i ugao EKQ prav, biće kvadrat na QE dvaput veći od kvadrata na EK [I.47]. Zatim, pošto je LK jednako KE i ugao LKE prav, biće kvadrat na EL dvaput veći od kvadrata na EK [I.47]. A dokazano je da je kvadrat na QE dvaput veći od kvadrata na EK. Prema tome je kvadrat na LE jednak kvadratu na EQ; dakle i LE je jednako EQ. Iz istih razloga je i LQ jednako QE. Dakle je trougao LEQ jednakostran. Slično se dokazuje da je jednakostran i svaki od preostalih trouglova čije su osnovice strane kvadrata EZHQ i vrhovi u tačkama L, M. Na ovaj način je konstruisan oktaedar omeđen sa osam jednakostranih trouglova.
Treba ga obuhvatiti datom sferom i dokazati da je kvadrat na prečniku sfere dvaput veći od kvadrata na ivici oktaedra.
Pošto su tri duži LK, KM, KE jednake među sobom, to će polukrug nacrtan na LM proći i kroz tačku E. Iz istih razloga, ako se, pri nepokretnom LM, polukrug obrne i ponovo vrati u početni položaj, on će proći i kroz tačke Z, H, Q i oktaedar će biti obuhvaćen sferom. Tvrdim da je to data sfera. Zaista, pošto je LK jednako KM, a KE je zajedničko i obuhvataju prave uglove, biće i osnovica LE jednaka osnovici EM [I.4]. I pošto je ugao LEM prav, jer je u polukrugu, biće kvadrat na LM dvaput veći od kvadrata na LE [I.47]. Zatim, pošto je AG jednako GB, biće AB dvaput veći od BG. No AB je prema BG kao kvadrat na AB prema kvadratu na BD. Prema tome je i kvadrat na AB dvaput veći od kvadrata na BD. A dokazano je da je i kvadrat na LM dvaput veći od kvadrata na LE. I kvadrat na DB jednak je kvadratu na LE, jer je uzeto EQ jednako DB. Prema tome je kvadrat na AB jednak kvadratu na LM, dakle, i AB je jednako LM. A kako je AB prečnik date sfere, biće i LM prečnik date sfere.
Na ovaj način je oktaedar obuhvaćen datom sferom i u isto vreme je dokazano da je kvadrat na prečniku sfere dvaput veći od kvadrata na ivici oktaedra. A to je trebalo dokazati.