Lema
Dokazati da je AB prema BG kao kvadrat na AD prema kvadratu na DG.
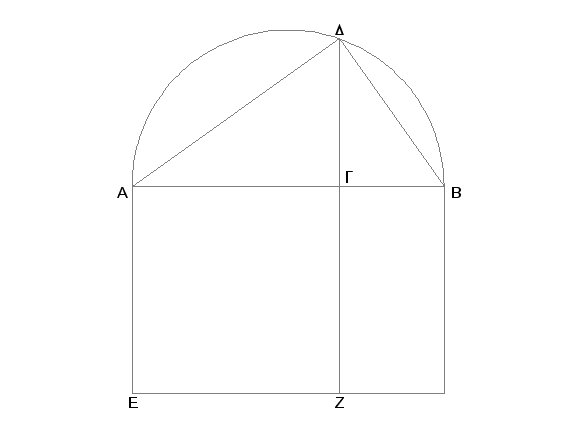
Zaista, uočimo sliku polukruga, povucimo DB, pa nacrtajmo kvadrat EG na AG i dopunimo paralelogram ZB. Pošto je sad, zbog jednakosti uglova u trouglovima DAB i DAG, duž BA prema duži AD kao DA prema AG [VI.8, VI.4], biće pravougaonik obuhvaćen od BA i AG jednak kvadratu na AD [VI.17]. I pošto je AB prema BG kao EB prema BZ [VI.1] i EB je pravougaonik obuhvaćen od BA i AG, jer je EA jednako AG, a BZ je pravougaonik obuhvaćen od AG i GB, biće AB prema BG kao pravougaonik obuhvaćen od BA i AG prema pravougaoniku obuhvaćenom od AG i GB. I pravougaonik obuhvaćen od BA i AG jednak je kvadratu na AD, a obuhvaćen od AG i GB - kvadratu na DG, jer je normala DG srednja proporcionala otsečaka AG i GB osnovice zato što je ugao ADB prav [VI.8, Posledica]. I prema tome je AB prema BG kao kvadrat na AD prema kvadratu na DG. A to je trebalo dokazati.