Ako je duž podeljena neprekidno, biće kvadrat na zbiru većeg dela i polovine cele duži jednak petostrukom kvadratu na toj polovini.

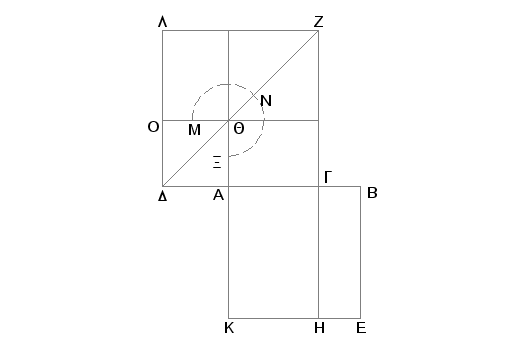
Neka je duž AB tačkom G podeljena neprekidno i neka je AG veći deo; produžimo duž GA preko A za duž AD i neka je AD jednako polovini AB. Tvrdim da je kvadrat na GD jednak petostrukom kvadratu na DA.
Zaista, konstruišimo na AB i na DG kvadrate AE i DZ i u DZ nacrtajmo uobičajenu sliku i produžimo ZG do H. Pošto je AB tačkom G podeljeno neprekidno, biće pravougaonik obuhvaćen od AB i BG jednak kvadratu na AG [VI, Def. 3, VI.17]. No pravougaonik od AB i BG jednak je pravougaoniku GE, a kvadrat na AG jednak je kvadratu ZQ. Prema tome je GE, jednako ZQ. I pošto je BA dvostruko AD, i BA jednako KA, a AD jednako AQ, biće i KA dvostruko AQ. Ali KA je prema AQ kao GK prema GQ [VI.1], pa je, znači, GK dvostruko GQ. No i zbir LQ i QG je dvostruko GQ. A dokazano je da je i GE jednako QZ. Prema tome je ceo kvadrat AE jednak gnomonu MNX. I pošto je BA udvostručeno AD, biće kvadrat na BA četvorostruki kvadrat na AD, tj. AE četvorostruko DQ. Ali AE je jednako gnomonu MNX, pa prema tome je gnomon MNX četvorostruko AO. A ceo DZ je petostruko AO. No DZ je kvadrat na DG, a AO na DA, pa je stoga kvadrat na GD petostruki kvadrat na DA.
Na ovaj način, ako je duž podeljena neprekidno, biće kvadrat na zbiru većeg dela i polovine cele duži jednak petostrukom kvadratu na toj polovini. A to je trebalo dokazati.