9.
Prave paralelne istoj pravoj, koje se sa ovom ne nalaze u istoj ravni, paralelne su među sobom.
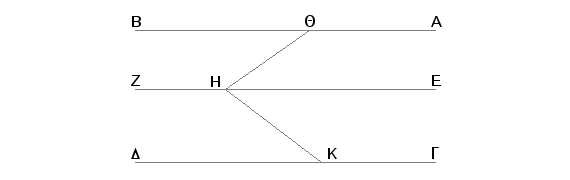
Zaista, neka je svaka od pravih AB i GD paralelna sa EZ, no neka se ne nalaze u istoj ravni. Tvrdim, da su AB i GD paralelne.
Zaista, uzmimo na EZ proizvoljnu tažku H i iz te tačke povucimo u ravan pravih EZ i AB pod pravim uglom prema EZ pravu HQ, a u ravni pravih ZE i GD pravu HK pod pravim uglom prema EZ. Pošto je EZ upravna na svakoj od pravih HQ i HK, ona je upravna i na ravni što prolazi kroz prave HQ i HK [XI.4]. I prava EZ je paralelna sa pravom AB. Prema tome je i prava AB upravna na ravni QHK [XI.8]. Iz istih razloga je i prava GD upravna na ravni QHK. Na ovaj način je svaka od AB i GD upravna na ravni QHK. No ako su dve prave upravne na istoj ravni, one su paralelne [XI.6]. Na ovaj način prava AB je paralelna sa GD. A to je trebalo dokazati.