5.
Tri prave sa zajedničkom tačom su u istoj ravni, ako postoji prava koja prolazi kroz tu zajedničku tačku i upravna je na svakoj od tih pravih.
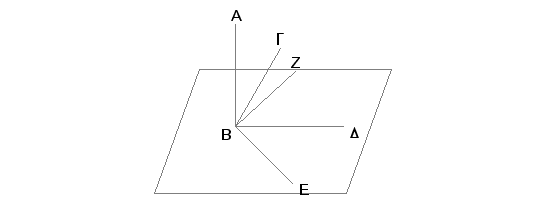
Zaista, neka prava AB koja prolazi kroz zajedničku tačku B pravih BG, BD, BE stoji pod pravim uglom prema svakoj od njih. Tvrdim, da su BG, BD, BE u istoj ravni.
Zaista, ako to nije tako, onda je moguće, da BD i BE budu u osnovnoj ravni, a BG van te ravni. Konstruišimo onda kroz AB i BG ravan. U preseku sa osnovnom ravni ona čini pravu [XI.3]. Neka to bude prava BZ. Znači da su tri prave AB, BG, BZ u istoj ravni koja prolazi kroz AB i BG. A kako je AB upravna prema svakoj od BD i BE, ona je upravna i na ravni pravih BD i BE [XI.4]. No ravan pravih BD i BE je osnovna ravan. Prema tome je AB upravna na osnovnoj ravni. A tada je AB upravna na svakoj pravoj u toj ravni koja seče pravu AB [XI, Def. 3]. No nju seče i prava BZ, koja se takođe nalazi u osnovnoj ravni. Prema tome je ugao ABZ prav ugao. Ali je pretpostavljeno da je i ugao ABG prav. Prema tome je ugao ABZ jednak uglu ABG. I oni se nalaze u istoj ravni. A to je nemoguće. Dakle prava BG neće biti u nekoj ravni iznad osnovne. Prema tome se tri prave BG, BD, BE nalaze u istoj ravni.
Na ovaj način, tri prave sa zajedničkom tačkom su u istoj ravni, ako postoji prava koja prolazi kroz tu zajedničku tačku i upravna je na svakoj od tih pravih. A to je trebalo dokazati.