37.
Ako su četiri duži proporcionalne, proporcionalni su i slični paralelepipedi, slično konstruisani na tim dužima. I ako su slični paralelepipedi, a slično konstruisani na dužima, proporcionalni, onda su proporcionalne i same ove duži.
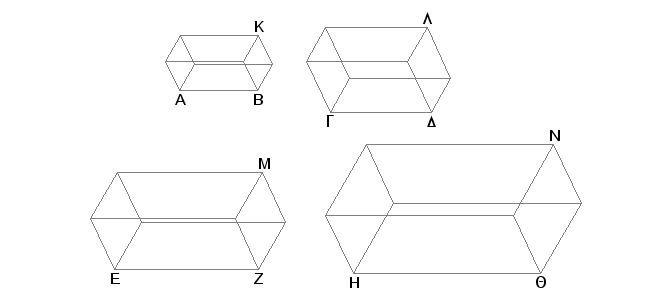
Neka su AB, GD, EZ, HQ četiri proporcionalne duži, naime: AB je prema GD kao EZ prema HQ. Konstruišimo na AB, GD, EZ i HQ slične i slično konstruisane paralepipede KA, LG, ME i NH. Tvrdim da je KA prema LG kao ME prema NH.
Zaista, pošto je paralelepiped KA sličan LG, biće razmera KA prema LG triput viša od razmere AB prema GD [XI.33]. Iz istih razloga je razmera ME prema NH triput viša od razmere EZ prema HQ [XI.33]. A kako je AB prema GD kao EZ prema HQ, biće i AK prema LG kao telo ME prema NH.
No neka je telo AK prema telu LG kao telo ME prema NH. Tvrdim, da je duž AB prema GD kao EZ prema HQ.
Zaista, pošto je, opet, razmera KA prema LG triput viša od razmere AB prema GD [XI.33], a i ME je prema NH u razmeri triput višoj od razmere EZ prema HQ [XI.33], a KA je prema LG kao ME prema NH, biće i AB prema GD kao EZ prema HQ.
Na ovaj način, ako su četiri duži proporcionalne, onda su i tako dalje, kao u tekstu teoreme. A to je trebalo dokazati.