30.

Paralelepipedi sa istom osnovom, istom visinom i bočnim ivicama čiji krajevi nisu na istim pravima - jednaki su među sobom.

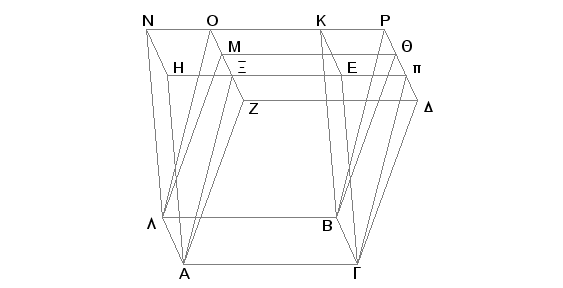
Neka su paralelepipedi GM i GN na istoj osnovi AB, sa istom visinom i bočnim ivicama AZ, AH, LM, LN, GD, GE, BQ i BK sa krajevima koji nisu na istim pravima. Tvrdim, da je telo GM jednako telu GN.
Zaista, produžimo NK i DQ i neka se one susreću u tački P. Produžimo još ZM i HE do O i p, povucimo AX, LO, Gp, BP. Sad je telo GM sa osnovom paralelogramom AGBL i naspramnom stranom ZDQM jednako telu GO sa osnovom paralelogramom AGBL i naspramnom stranom XpPO, jer su ona na istoj osnovi AGBL, sa istom visinom i bočnim ivicama AZ, AX, LM, LO, GD, Gp, BQ, BP, čiji su krajevi na istim pravama ZO i DP [XI.29]. No GO sa osnovom paralelogramom AGBL i naspramnom stranom XpPO jednako je telu GN sa osnovom paralelogramom AGBL i naspramnom stranom HEKN pošto su ona na istoj osnovi AGBL, sa istom visinom i bočnim ivicama AH, AX, GE, Gp, LN, LO, BK, BP čiji su krajevi na istim pravama Hp i NP. Pa prema tome je telo GM jednako telu GN.
Na ovaj način, paralelepipedi sa istom osnovom, istom visinom i bočnim ivicama čiji krajevi nisu na istim pravima - jednaki su među sobom.