29.
Paralelepipedi sa istom osnovom, istom visinom i bočnim ivicama čiji su krajevi na istim pravima - jednaki su među sobom.
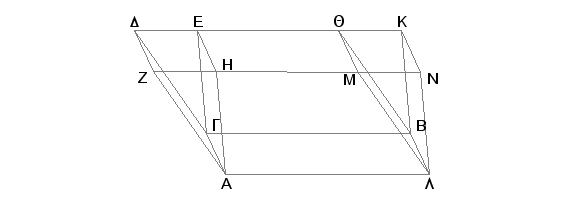
Neka su paralelepipedi GM i GN na istoj osnovi AB, sa istom visinom, i bočnim ivicama AH, AZ, LM, LN, GD, GE, BQ, BK sa krajevima na istim pravima ZN i DK. Tvrdim da je telo GM jednako telu GN. Zaista, pošto je svaki od četvorouglova GQ i GK paralelogram, duž GK je jednaka svakoj od duži DQ i EK [I.34]. Prema tome je duž DQ jednaka duži EK. Kako je EQ njihov zajednički deo, biće ostatak DE jednak ostatku QK. Prema tome je i trougao DGE jednak trouglu QBK [I.8, I.4], a paralelogram DH - paralelogramu QN [I.36]. Iz istih razloga je i trougao AZH jednak trouglu MLN. A i paralelogram GZ jednak paralelogramu BM, i paralelogram GH - paralelogramu BN, jer su naspramni. I na taj način je prizma, obuhvaćena sa dva trougla AZH i DGE i sa tri paralelograma AD, DH i GH, jednaka prizmi obuhvaćenoj sa dva trougla MLN i QBK i tri paralelograma BM, QN i BN. Dodajmo zajedničko telo, čija je osnova paralelogram AB i naspramna strana HEQM, pa će tada ceo paralelepiped GM biti jednak celom paralelepipedu GN.
Na ovaj način, paralelepipedi sa istom osnovom, istom visinom i sa bočnim ivicama, čiji su krajevi na istim pravima - jednaki su među sobom. A to je trebalo dokazati.