22.

Ako postoje tri ravna ugla, od kojih je zbir dva proizvoljno uzeta, veći od preostalog, a obrazuju ih jednake duži onda je moguće konstruisati trougao od duži koje spajaju krajeve jednakih duži.

Neka postoje tri ravna ugla ABG, DEZ, HQK, kod kojih je zbir dva veći od preostalog, naime: ABG i DEZ veći je od HQK, a zbir DEZ i HQK od ABG i zbir HQK i ABG od DEZ. I neka su duži AB, BG, DE, EZ, HQ, QK jednake. Pa spojimo AG, DZ, HK. Tvrdim, da je moguće od duži, koje su jednake: AG, DZ, HK sastaviti trougao, tj. da je zbir od dve, proizvoljno uzete, duži od AG, DZ, HK veći od preostale.

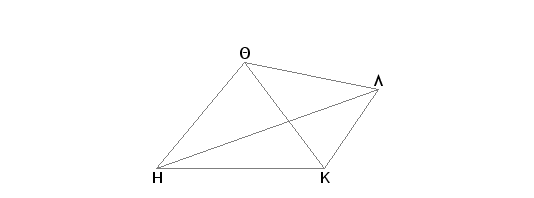
Ako su uglovi ABG, DEZ, HQK jednaki među sobom, jasno je, da su tada i duži AG, DZ, HK jednake među sobom, a od jedakih duži AG, DZ, HK moguće je sastaviti trougao. Ako to nije tako, neka uglovi nisu jednaki. Konstruišimo na duži QK, kod tačke Q, ugao KQL jednak uglu ABG, odmerimo duž QL jednaku jednoj od duži AB, BG, DE, EZ, HQ, QK i spojimo KL, HL. Pošto su dve duži AB i BG jednake dvema dužima KQ, QL i ugao kod tačke B jednak uglu KQL, biće i osnovica AG jednaka osnovici KL [I.4]. I pošto je zbir uglova ABG i HQK veći od ugla DEZ, a ugao ABG jednak je uglu KQL, biće ugao HQL veći od ugla DEZ. A pošto su dve duži HQ i QL jednake dvema dužima DE, EZ i ugao HQL veći od ugla DEZ, biće i osnovica HL veća od osnovice DZ [I.24]. Ali zbir od HK i KL je veći od HL [I.20], pa prema tome i zbir HK i KL je veći od DZ. No KL je jednako duži AG. Na ovaj način je zbir od AG i HK veći od preostale DZ. Slično se dokazuje, da je i zbir od AG i DZ veći od HK, pa i zbir od DZ i HK veći od AG.
Na ovaj način je moguće od tri duži, jednake sa AG, DZ, HK, konstruisati trougao. A to je trebalo dokazati.