20.

Ako je rogalj obuhvaćen sa tri ravna ugla, zbir ma koja dva od njih je veći od trećeg.

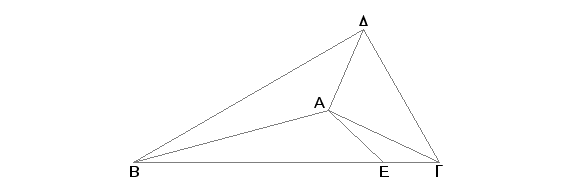
Zaista, neka je rogalj kod tačke A obuhvaćen sa tri ravna ugla: BAG, GAD, DAB. Tvrdim da je zbir ma koja dva od uglova BAG, GAD, DAB veći od trećeg.
Ako su uglovi BAG, GAD, DAB jednaki jedan drugom, jasno da je zbir bilo koja dva od njih veći od trećeg. Ako nisu jednaki, neka je najveći ugao BAG. Konstruišimo u ravni BAG, na pravoj AB kod tačke A, ugao BAE jednak uglu DAB, odmerimo duž AE jednaku AD i neka prava BEG kroz tačku E preseca prave AB i AG u tačkama B i G, pa spojimo BD i DG. I pošto je duž DA jednaka duži AE, a AB je zajednička, biće dve jednake dvema. A i ugao DAB jednak je uglu BAE. Prema tome je i osnovica DB jednaka osnovici BE [I.4]. I pošto je zbir BD i DG veći od BG [I.20], od kojih je BD, kako je dokazano, jednako BE, biće i ostatak DG veći od ostatka EG. I pošto je DA jednako AE, a AG je zajednička, i osnovica DG je veća od osnovice EG, biće ugao DAG veći od ugla EAG [I.25]. Dokazano je međutim da je ugao DAB jednak uglu BAE. Prema tome je zbir uglova DAB i DAG veći od ugla BAG. Slično se dokazuje da su i drugi, uzeti po dva veći od trećeg.
Na ovaj način, ako je rogalj obuhvaćen sa tri ravna ugla, zbir ma koja dva od njih je veći od trećeg. A to je trebalo dokazati.