2.
Ako dve prave seku jedna drugu, one su u istoj ravni; i svaki trougao je u istoj ravni.
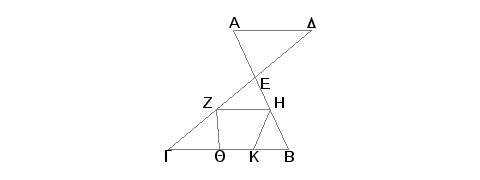
Neka dve prave AB i GD seku jedna drugu u tački E. Tvrdim da su AB i GD u istoj ravni i svaki trougao je u istoj ravni.
Zaista, uzmimo na pravima EG i EB neke tačke Z i H i povucimo GB, ZH i ZQ, HK. Prvo tvrdim, da je trougao EGB u istoj ravni. Zaista, ako se jedan deo trougla EGB, ZQG ili HBK, nalazi u osnovnoj ravni, a drugi je izdignut van te ravni, onda se i jedan deo pravih EG i EB nalazi u osnovnoj ravni, a drugi deo van te ravni. A ako se deo ZGBH trougla EGB nalazi u osnovnoj ravni, a ostali deo van, onda se i kod pravih EG i EB jedan deo nalazi u osnovnoj ravni, a drugi van ravni. A to je, prema dokazanom, besmisleno [XI.1]. Prema tome je trougao EGB u istoj ravni. I svaka od pravih EG i EB biće u istoj ravni sa trouglom EGB, a biće u ravni EG i EB i prave AB i GD [XI.1].
Na ovaj način prave AB i GD su u istoj ravni. A to je trebalo dokazati.