19.
Ako su dve ravni, koje se seku, normalne na nekoj ravni, biće i njihov presek normalan na istoj ravni.
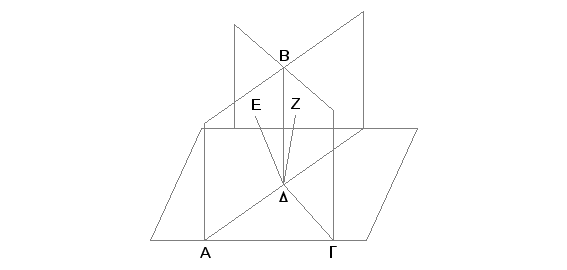
Neka su dve ravni, AB i BG, normalne na osnovnoj ravni, a njihov presek neka bude prava BD. Tvrdim, da je BD normalna na osnovnoj ravni.
Zaista, neka nije tako. Iz tačke D u ravni AB povucimo pravu DE upravnu na AD, a u ravni BG pravu DZ upravnu na GD. Pošto je AB ravan upravna na osnovnoj ravni i u ravni AB je povučena prava DE upravna na zajedničkom preseke ravni AB i osnovne ravni, biće prava DE upravna na osnovnoj ravni [XI, Def. 4]. Slično se dokazuje da je i prava DZ upravna na osnovnoj ravni. Prema tome iz iste tačke D osnovne ravni sa iste strane te ravni povučene su dve normale na tu ravan. A to je nemoguće [XI.13]. Znači iz tačke D osnovne ravni ne može biti druge normale sem BD, preseka ravni AB i BG.
Na ovaj način, ako su dve ravni, koje se seku, normalne na nekoj ravni, biće i njihov presek normalan na toj ravni. A to je trebalo dokazati.