9.
Oko datog kvadrata opisati krug.
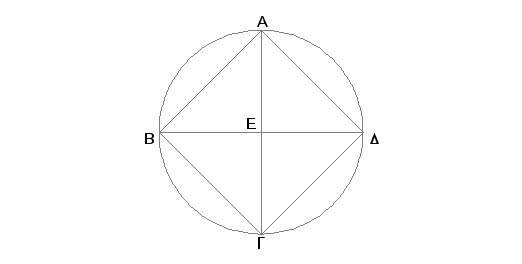
Neka je dat kvadrat ABGD. Treba oko kvadrata ABGD opisati krug.
Neka se prave, što spajaju, AG i BD seku u tački E.
Kako je DA jednako AB, a AG zajedničko, onda su dve strane DA i AG jednake dvema stranama BA i AG, a i osnovica DG jednaka je osnovici BG, tada biće i ugao DAG jednak uglu BAG [I.8], pa prema tome ugao DAB polovi prava AG. Na sličan način se dokazuje da svaki od uglova ABG, BGD, GDA polove prave AG i DB. A kako je ugao DAB jednak uglu ABG, a ugao EAB je polovina ugla DAB i ugao EBA je polovina ugla ABG, onda je i ugao EAB jednak uglu EBA, pa je tada i strana EA jednaka strani EB [I.6]. Na sličan način se dokazuje da je svaka od pravih EA, EB, jednaka svakoj od EG, ED. Prema tome su četiri prave EA, EB, EG, ED međusobno jednake. Tada će krug nacrtan sa centrom u E jednim od rastojanja do tačaka A, B, G, D proći i kroz ostale tačke i biće opisan oko kvadrata ABGD. Neka je ovaj nacrtan kao ABGD.
Na ovaj način je oko datog kvadrata opisan krug. A to je trebalo izvesti.