5.
Oko datog trougla opisati krug.
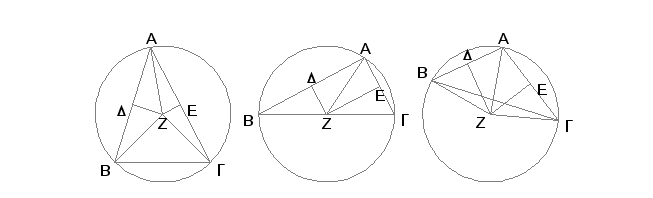
Neka je dat trougao ABG. Treba oko datog trougla opisati krug.
Prepolovimo prave AB, AG tačkama D, E [I.10] i kroz tačke D, E povucimo prave DZ, EZ pod pravim uglovima prema pravim AB i AG. One se seku ili u trouglu ABG, ili na pravoj BG ili s druge strane prave BG, van trougla.
Neka se, prvo, seku u trouglu u Z, pa povucimo ZB, ZG, ZA. Tada je, pošto je AD jednako DB, a DZ zajedničko i pod pravim uglovima, osnovica AZ jednaka osnovici ZB [I.4]. Na sličan način se dokazuje da je GZ jednako AZ, pa je prema tome i ZB jednako ZG. Dakle tri prave ZA, ZB, ZG su međusobno jednake. Prema tome će krug sa centrom u Z opisan sa rastojanjem do jedne od tačaka A, B, G proći i kroz ostale tačke i biće krug opisan oko trougla ABG. Neka je on opisan kao ABG.
Uzmimo sad da se DZ i EZ seku na pravoj BG u Z, kao što je to slučaj na drugoj slici, pa povucimo AZ. Na sličan način se dokazuje da će tačka Z biti centar kruga opisanog oko trougla ABG.
Najzad, neka se DZ i EZ seku u tački Z van trougla ABG, kao što je to nacrtano na trećoj slici, pa povucimo AZ, BZ, GZ. Kako je opet AD jednako DB, a DZ je zajednička strana pod pravim uglovima, osnovica AZ jednaka je osnovici BZ [I.4]. Na sličan način dokazuje se da je GZ jednako AZ, prema tome je i BZ jednako ZG. Prema tome će opet krug sa centrom u Z opisan sa rastojanjem do jedne od tačaka A, B, G proći i kroz ostale tačke i biti opisan oko trougla ABG.
Na ovaj način oko datog trougla je opisan krug. A to je trebalo izvesti.