14.

Oko datog petougla, sa jednakim stranama i jednakim uglovima opisati krug.

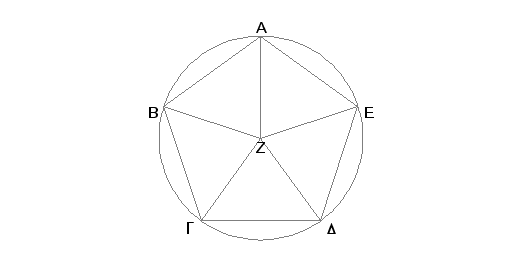
Neka je dat petougao ABGDE sa jednakim stranama i jednakim uglovima. Treba oko petougla ABGDE opisati krug.
Prepolovimo svaki od uglova BGD i GDE pravom GZ odnosno DZ i kroz taču Z, koja je presek pravih, povucimo ka tačkama B, A, E prave ZB, ZA, ZE. Na sličan način, kao i ranije, dokazuje se da i svaki od uglova GBA, BAE, AED polove prava ZB, odnosno, ZA, odnosno ZE. Kako je ugao BGD jednak uglu GDE, a i polovina ugla BGD, ugao ZGD, jednaka polovini ugla GDE, uglu GDZ, biće i ugao ZGD jednak uglu ZDG. Znači da je i strana ZG jednaka strani ZD [I.6]. Na sličan način se dokazuje da je i svaka od pravih ZB, ZA, ZE jednaka svakoj od strana ZG i ZD. Prema tome su pet pravih ZA, ZB, ZG, ZD, ZE međusobno jednake. Tada će krug nacrtan sa centrom u Z sa jednim od rastojanja ZA, ZB, ZG, ZD, ZE proći i kroz ostale tčke i biti opisan. Neka je opisan kao ABGDE.
Na ovaj način je oko datog petougla, sa jednakim stranama i jednakim uglovima, opisan krug. A to je trebalo izvesti.