8.
Ako su u dva trougla dve strane jednake dvema odgovarajućim stranama drugog, i osnovice im jednake, moraju biti jednaki i uglovi koje obrazuju jednake strane.
Neka ABG i DEZ budu dva trougla, kod kojih su dve strane AB i AG jednake dvema odgovarajućim stranama AE i DZ, naime AB strane DE i AG strani DZ, i osnovica BG jednaka osnovici EZ. Tvrdim da je tada ugao BAG jednak uglu EDZ.
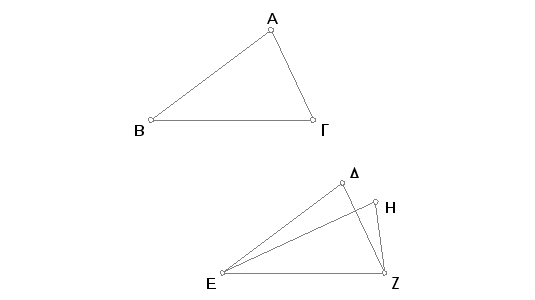
Ako se trougao ABG položi na trougao DEZ, tačka B će se poklopiti sa tačkom E, prava BG pasti na pravu EZ i tačka G poklopiti sa Z zbog jednakosti BG i EZ. A kad se duž BG poklopi sa EZ, onda će se poklopiti i BA, GA sa ED, DZ. Jer, ako se osnovica BG poklopi sa osnovicom EZ, a strane BA, AG se ne bi poklopile sa stranma ED, DZ, već bi otstupale od njih kao EH, HZ, onda bi bile povučene iz svake od dve različite tačke, koje se nalaze sa iste strane date duži ka njenim krajevima po dve duži, tako da duži sa istim krajevima budu međusobno jednake. A to je nemoguće [I. 7]. Nemoguće je prama tome da se osnovice BG i EZ poklapaju, a da se strane BA, AG ne poklapaju sa stranama ED, DZ. Znači one se poklapaju, a tada se ugao BAG poklapa sa uglom EDZ i njemu je jednak.
Na ovaj način, ako su u dva trougla dve strane jednog jednake dvema odgovarajućim stranama drugog, a i osnovice im jednake, moraju biti jednaki i uglovi koje obrazuju jednake strane. A to je trebalo dokazati.