5.
Kod jednakokrakih trouglova uglovi su na osnovici jednaki međusobno, a u slučaju produženja jednakih strana uglovi pod osnovicom takođe moraju biti jednaki međusobno.
Neka je ABG jednakokraki trougao sa krakom AB jednakim kraku AG i neka su prave BD i GE produženja krakova AB i AG [Post. 2]. Tvrdim da je ugao ABG jednak uglu AGB i ugao GBD uglu BGE.
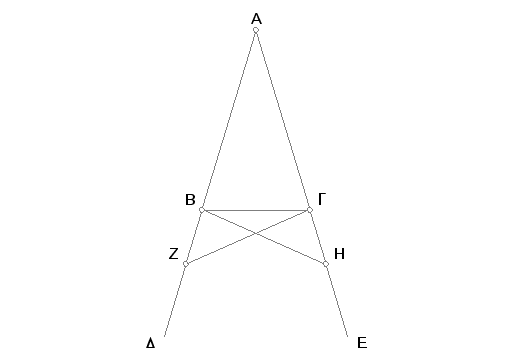
Neka se na pravoj BD uzme proizvoljna tačka Z i prenese na veću duž AE duž AH jednaka manjoj AZ [I. 3], pa zatim povuku prave ZG i HB [Post. 1],
Pošto je AZ jednako AH i AB jednako AG, tj. pošto su dve strane ZA, AG jednake odgovarajućim dvema stranama HA, AB i čine zajednički ugao ZAH, to je osnovica ZG jednaka osnovici HB, i trougao AZG jednak trouglu AHB i ostali uglovi jednaki odgovarajućim ostalim uglovima koji leže spram jednakih strana, naime ugao AGZ uglu ABH i ugao AZG uglu AHB [I. 4]. I pošto je cela duž AZ jednaka celoj duži AH, a duž AB je jednaka duži AG, biće i ostatak, tj. duž BZ, jednak ostatku - duži GH. A ranije je pokazano, da je ZG jednako HB. Prema tome dve strane BZ, ZG jednake su odgovarajućim dvema stranama GH, HB i ugao BZG jednak je uglu GHB, a osnovica je ista BG; trougao BZG biće jednak trouglu GHB, i ostali uglovi biće jednaki odgovarajućim uglovima što leže spram jednakih strana; ugao ZBG biće prema tome jednak uglu HGB i ugao BGZ uglu GBH. A pošto je, kako je pokazano, ceo ugao ABH jednak celom uglu AGZ, a ugao GBH jednak uglu BGZ, to će i ostatak - ugao ABG, biti jednak ostatku - uglu AGB; a ovi uglovi leže na osnovici trougla ABG. A ranije je pokazano, da je ugao ZBG jednak uglu HGB, a ovi se nalaze pod osnovicom.
Tako su kod jednakokrakih trouglova uglovi na osnovici jednaki međusobno, a u slučaju produženja jednakih strana uglovi pod osnovicom takođe moraju biti jednaki međusobno. A to je trebalo dokazati.