47.
Kod pravouglih trouglova je kvadrat na strani spram pravog ugla (na hipotenuzi) jednak kvadratima na stranama koje obrazuju prav ugao (na katetama).
Neka je ABG pravougli trougao sa pravim uglom BAG. Tvrdim da je kvadrat na BG jednak kvadratima na BA i AG.
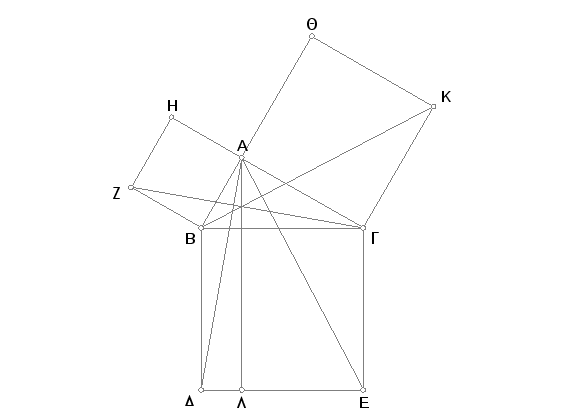
Neka se na BG konstruiše kvadrat BDEG, a na BA, AG kvadrati HB, QG [I. 46], kroz tačku A povuče prava AL paralelna svakoj od pravih BD, GE, a zatim povuku prave AD, ZG. Pošto je svaki od uglova BAG, BAH prav, to prave AG, AH povučene nad pravom BA, kroz istu njenu tačku A, a sa raznih strana, čine susedne uglove jednake dvama pravim uglovima, pa su stoga prave GA i AH u istoj pravoj [I. 14]. Iz istog razloga su i prave BA i AQ u istoj pravoj. Ugao DBG jednak je uglu ZBA, jer je svaki od njih prav. A kad se doda svakom od njih ugao ABG, biće ceo ugao DBA jednak celom uglu ZBG [A. 2]. Pošto je strana DB jednaka strani BG, a ZB strani BA, to su dve strane DB, BA jednake stranama ZB, BG, i to odgovarajućim, i ugao DBA jednak uglu ZBG, a tada je i osnovica AD jednaka osnovici ZG, i trougao ABD jednak trouglu ZBG [I. 4]. A paralelogram BL je dvaput veći od trougla ABL, jer imaju istu osnovicu BD i između istih su paralelnih BD, AL [I. 41]. I kvadrat HB je dvaput veći od trougla ZBG, jer i oni imaju istu osnovicu ZB i između istih su paralela ZB, HG [I. 41]. (A dvostruko od jednakog jednako je [A. 5]). Prema tome je paralelogram BL jednak kvadratu HB. Na sličan način se, pomoću povučenih pravih AE, BK, može dokazati da je paralelogram GL jednak kvadratu QG. Prema tome je ceo kvadrat BDEG jednak dvama kvadratima HB, QG [A. 2]. A kvadrat BDEG je konstruisan na BG, a kvadrati HB, QG na BA, AG. Prema tome je kvadrat na strani BG jednak kvadratima na stranama BA, AG.
Dakle, kod pravouglih trouglova je kvadrat na strani spram pravog ugla (na hipotenuzi) jednak kvadratima na stranama koje obrazuju prav ugao (na katetama). A to je trebalo dokazati.