45.
U datom pravolinijskom uglu konstruisati paralelogram jednak datoj pravolinijskoj slici.
Neka je ABGD data pravolinijska slika i E dati pravolinijski ugao. Treba u datom pravolinijskom uglu E konstruisati paralelogram jednak datoj pravolinijskoj slici.
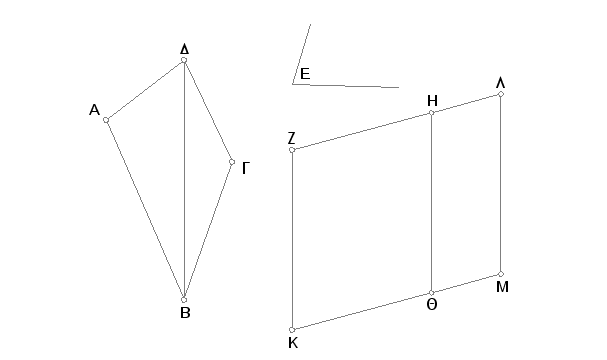
Povuče se DB i konstruiše se u uglu QKZ, koji je jednak E, paralelogram ZQ jednak trouglu ABD [I. 42]; i doda se u uglu HQ M, koji je jednak uglu E, na pravoj HQ paralelogram HM jednak trouglu DBG [I. 44]. Pošto je ugao E jednak svakom od uglova QKZ, HQM, onda je ugao QKZ jednak uglu HQM [A. 1]. Ako se svakom od ovih doda ugao KQH, biće uglovi ZKQ , KQH jednaki uglovima KQH, HQM. Ali kako su uglovi ZKQ, KQH jednaki dvama pravim uglovima [I. 29], to su i uglovi KQH, HQM jednaki dvama pravim uglovima. Pošto dve prave KQ, QM sa pravom HQ i u istoj tački Q, no ne sa iste strane ove prave, čine dva susedna ugla jednaka dvama pravim uglovima, to će KQ i QM ležati u istoj pravoj [I. 14]. I pošto je QH transverzala za paralelne KM, ZH, to su unutrašnji naizmenični uglovi MQH, QHZ jednaki međusobno [I. 29]. Ako se svakom od ovih doda ugao QHL, biće uglovi MQH, QHL jednaki uglovima QHZ, QHL [A. 2]. Ali kako su uglovi MQH, QHL jednaki dvama pravim uglovima [I. 29], to su i uglovi QHZ, QHL jednaki dvama pravim uglovima [A. 1]; prema tome su i prave ZH i HL u istoj pravoj [I. 14]. I pošto je ZK jednako i paralelno QH [I. 34], a QH isto tako pravoj ML, to je i KZ jedanko i paraleleno ML [A. 1, I. 30]. Neka prave KM, ZL spajaju te prave, tada su KM, ZL jednake i paralelne [I. 33], a KZLM je paralelogram. I pošto je trougao ABD jednak paralelogramu ZQ, a DBG paralelogramu HM, to je cela pravolinijska slika ABGD jednaka celom paralelogramu KZLM.
Na ovaj način je u pravolinijskom uglu ZKM, koji je jednak datom pravolinijskom uglu E, konstruisan paralelogram KZLM jednak datoj pravolinijskoj slici ABGD. A to je trebalo izvesti.