4.
Ako su kod dva trougla dve strane jednog jednake odgovarajućim dvema stranama drugog i ako su jednaki uglovi koje obrazuju jednake strane, mora i osnovica biti jednaka osnovici, jedan trougao mora biti jednak drugom trouglu i ostali uglovi moraju biti jednaki ostalim uglovima i to odgovarajući, naime oni koji leže spram jednakih strana.
Neka su kod dva trougla ABG i DEZ dve strane, AB i AG, jednake stranama DE, DZ i to odgovarajuće, tj. AB jednaka DE i AG jednaka DZ i neka je ugao BAG jednak uglu EDZ. Tvrdim da je osnovica BG jednaka osnovici EZ, trougao ABG jednak trouglu DEZ i ostali uglovi jednaki ostalim uglovima, i to odgovarajući, tj. oni koji se nalaze spram jednakih strana, tj. ugao ABG jednak uglu DEZ i ugao AGB uglu DZE.
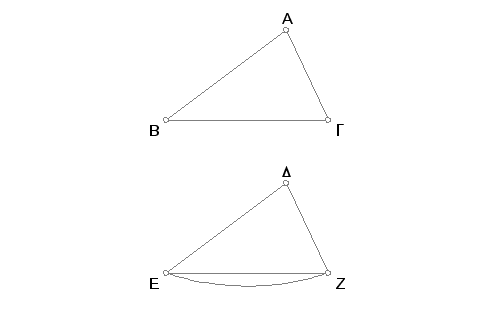
Ako se trougao ABG položi na trougao DEZ tako da tačka A padne u tačku D, a da duž AB ide po duži DE, tada će se tačka B poklopiti sa tačkom E zbog jednakosti AB i DE. Pošto se AB poklapa sa DE, mora prava AG ići u pravcu DZ zbog jednakosti uglova BAG i EDZ. Takođe će se poklopiti tačke G i Z, zbog jednakosti AG DZ. Ali se i B poklapa sa E. Otuda sledi da će se osnovica BG poklopiti sa osnovicom EZ, jer ako bi se B poklapao sa E, i G sa Z, a osnovica BG ne bi poklapala sa EZ, tada bi dve prave ograničavale oblast, a to je nemoguće. Prema tome i osnovica BG poklopiće se sa osnovicom EZ i biće sa njom jednaka [A. 4]. A i ceo trougao ABG će se poklopiti i biti jednak celom trouglu DEZ i ostali uglovi će se poklopiti i biti jednaki ostalim uglovima, naime ugao ABG jednak uglu DEZ i ugao AGB uglu DZE.
Na ovaj način, ako su kod dva trougla dve strane jednog jednake odgovarajućim dvema stranama drugog i jednaki uglovi koje obrazuju jednake strane, mora i osnovica biti jednaka osnovici, jedan trougao mora biti jednak drugom trouglu i ostali uglovi moraju biti jednaki ostalim uglovima i to odgovarajući, naime oni koje leže spram jednakih strana. A to je trebalo dokazati.