34.
Kod paralelograma su naspramne strane i uglovi jednaki međusobno i dijagonala ga polovi.
Neka je AGDB paralelogram i BG njegova dijagonala. Tvrdim da su kod paralelograma AGDB naspram\-ne strane i uglovi jednaki međusobno i da ga dijagonala BG polovi.
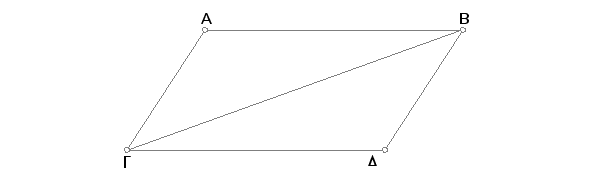
Pošto je AB paralelno GD i BG njihova transverzala, to su unutrašnji naizmenični uglovi ABG, BGD jednaki međusobno [I. 29]. Isto tako, pošto je AG paralelno BD i BG je njihova transverzala, unutrašnji naizmenični uglovi AGB, GBD jednaki su među sobom. Prema tome su ABG, BAGD dva trougla, koji imaju dva ugla ABG, BGA jednaka sa dva ugla BGD, GBD i jednu stranu jednaku jednoj strani i to spram jednakih uglova, naime zajedničku stranu BG. Zbog toga moraju biti jednake i ostale strane ostalim stranama, i to odgovarajućim, i preostali ugao preostalom uglu [I. 26]. Prema tome je strana AB jednaka strani GD, strana AG strani BD i ugao BAG uglu GDB. Pošto je ugao ABG jednak uglu BGD, a ugao GBD uglu AGB, to je ceo ugao ABD jednak celom uglu AGD [A. 2]. A ranije je dokazano da je i ugao BAG jednak uglu GDB.
Prema tome su kod paralelograma naspramne strane i naspramni uglovi jednaki međusobno.
Još tvrdim da ga dijagonala polovi. Pošto je AB jednako GD, a BG je zajedničko, to su dve strane AB, BG jednake dvema stranama GD, BG, i to odgovarajućim, i ugao ABG je jednak uglu BGD. Zbog toga je osnovica AG jednaka osnovici DB i trougao ABG jednak trouglu BGD [I. 4].
Na ovaj način dijagonala BG polovi paralelogram AGDB. A to je trebalo dokazati.