32.
U svakom trouglu spoljašnji ugao obrazovan produženjem jedne strane jednak je dvama nesusednim unutrašnjim uglovima, a tri unutrašnja ugla trougla jednaki su dvama pravim uglovima.
Neka je ABG trougao i neka se produži jedna njegova strana BG do D. Tvrdim da je spoljašnji ugao AGD jednak dvama nesusednim unutrašnjim uglovima GAB, ABG i da su tri unutrašnja ugla ABG, BGA, GAB jednaka dvama pravim uglovima.
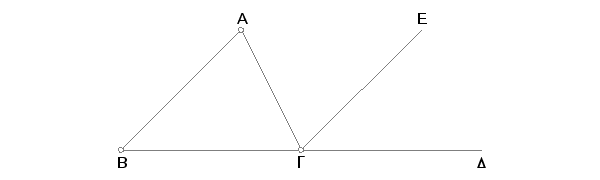
Neka se povuče kroz tačku G prava GE, paralelna pravoj AB [I. 31].
Pošto je AB paralelno GE, a prava AG njihova transverzala, to su unutrašnji naizmenični uglovi BAG, AGE jednaki međusobno [I. 29]. Isto tako, pošto je AB paralelna GE i BD je njihova transverzala, biće spoljašnji ugao EGD jednak unutrašnjem saglasnom ABG [I. 29]. Ranije je pokazano da je ugao AGE jednak uglu BAG. Prema tome je ceo ugao AGD jednak dvama unutrašnjim nesusednim uglovima BAG, ABG.
Kad se svakom od njih doda isti ugao AGB, biće uglovi AGD, AGB jednaki trima uglovima ABG, BGA jednaki trima uglovima ABG, BGA, GAB. Ali su AGD, AGB jednaki dvama pravim uglovima [I. 13], pa prema tome su i tri ugla ABG, BGA, GAB jednaki dvama pravim uglovima.
Na ovaj način, u svakom trouglu spoljašnji ugao obrazovan produženjem jedne strane jednak je dvama nesusednim unutrašnjim uglovima, a tri unutrašnja ugla trougla jednaki su dvama pravim uglovima. A to je trebalo dokazati.