29.
Ako prava seče dve paralelne prave, ona gradi unutrašnje naizmenične uglove jednake, spoljašnji ugao jednak odgovarajućem unutrašnjem uglu i dva unutrašnja ugla sa iste strane jednaka dvama pravim uglovima.
Neka prava EZ seče dve paralelne prave AB i GD. Tvrdim da ona gradi unutrašnje naizmenične uglove AHQ, HQD jednake i sa iste strane od nje spoljašnji ugao EHB jednak odgovarajućem unutrašnjem uglu HQD, i dva unutrašnja BHQ i HQD jednaka dvema pravim uglovima.
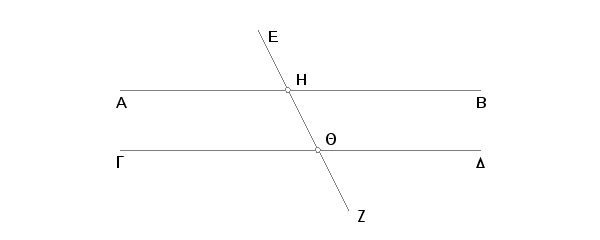
Ako pak ugao AHQ nije jednak uglu HQD, onda je jedan od njih veći. Neka je veći AHQ. Ako se doda svakom isti ugao BHQ, biće uglovi AHQ, BHQ veći od uglova BHQ, HQD. Ali uglovi AHQ, BHQ jednaki su sa dva prava [I. 13]. Prema tome su uglovi BHQ, HQD manji od dva prava ugla. Ali se sa uglovima manjim od dva prava ugla prave, produžene beskrajno, seku [Post. 5]. Pa prema tome AB, GD, produžene beskrajno, moraju da se seku. Ali one se ne seku jer su po pretpostavci paralelne. Prema tome nije ugao AHQ nejednak uglu HQD; znači da je jednak. No ugao AHQ jednak uglu EHB [I. 15], pa prema tome je ugao EHB jednak uglu HQD [A. 1]. Ako se doda svakom od ovih ugao BHQ, biće uglovi EHB, BHQ jednaki uglovima BHQ, HQD [A. 2]. Ali uglovi EHB, BHQ jednaki su dvama pravim uglovima [I. 13], pa prema tome su i uglovi BHQ, HQD jednaki dvama pravim uglovima.
Na ovaj način, ako prava seče dve paralelne prave, ona gradi unutrašnje naizmenične uglove jednake, spoljašnji ugao jednak odgovarajućem unutrašnjem uglu i dva unutrašnja ugla sa iste strane jednaka dvama pravim uglovima. A to je trebalo dokazati.