28.
Ako prava koja seče druge dve prave gradi sa iste svoje strane spoljašnji ugao jednak odgovarajućem unutrašnjem uglu ili dva unutrašnja ugla sa iste strane jednaka dvama pravim uglovima, ove dve prave paralelne su.
Neka prava EZ, koja seče dve prave AB, GD, tradi sa iste svoje strane spoljašnji ugao EHB jednak odgovarajućem unutrašnjem uglu HQD ili dva unutrašnja ugla sa iste strane BHQ i HQD jednaka dvama pravim uglovima. Tvrdim da je AB paralelno GD.
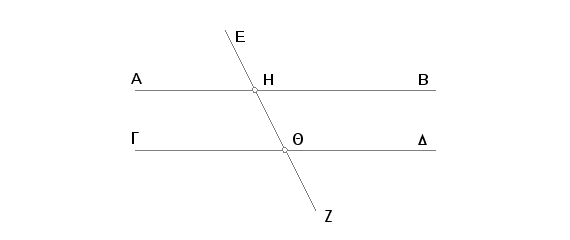
Pošto je ugao EHB jednak uglu HQD, a ugao EHB jednak uglu AHQ [I. 15], to je i ugao AHQ jednak uglu HQD, a oni su unutrašnji naizmenični, zbog čega je prava AB paralelna pravoj GD [I. 27].
S druge strane, pošto su uglovi BHQ, HQD jednaki sa dva prava, a uglovi AHQ, BHQ takođe jednaki sa dva prava [I. 13], to su uglovi AHQ, BHQ jednaki uglovima BHQ, HQD. Ako se oduzme zajednički ugao BHQ, biće ostatak, ugao AHQ, jednak ostatku, uglu HQD. A oni su unutrašnji naizmenični, pa zbog toga je prava AB paralelna, pravoj GD [I. 27].
Na taj način, ako prava koja seče druge dve prave gradi sa iste svoje strane spoljašnji ugao jednak odgovarajućem unutrašnjem ili dva unutrašnja ugla sa iste strane jednaka dvama pravim uglovima, ove dve prave paralelne su. A to je trebalo dokazati.