26.
Ako su kod dva trougla dva ugla jednog jednaki dvama uglovima drugog, i to odgovarajućim, i jedna strana jednog jednaka jednoj strani drugog ili ona na kojoj su jednaki uglovi ili ona što je spram jednog od jednakih uglova, onda su i ostale strane jednake ostalim stranama, i to odgovarajućim, a preostali ugao jednak je preostalom uglu.
Neka su kod dva trougla ABG, DEZ dva ugla ABG, BGA jednaki dvama uglovima DEZ, EZD, i to odgovarajućim, naime ugao ABG uglu DEZ i ugao BGA uglu EZD, i neka je jedna strana jednog jednaka jednoj strani drugog, prvo strana BG strani EZ na kojima su dati jednaki uglovi. Tvrdim da su tada i ostale strane jednake ostalim stranama, i to odgovarajućim, naime strana AB strani DE, strana AG strani DZ, a preostali ugao preostalom uglu, naime ugao BAG uglu EDZ.
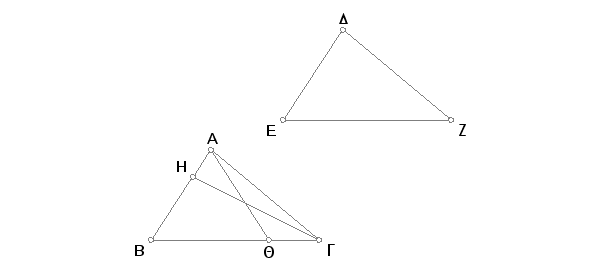
Ako pak AB nije jednako DE, onda je jedno od njih veće. Neka je veće AB; tada se prenese BH jednako DE i povuče se HG.
Pošto je BH jednako DE i BG jednako EZ, znači da su dve strane BH, BG jednake dvema stranama DE, EZ, i to odgovarajućim, i ugao HBG jednak uglu DEZ, dakle i osnovica HG jednaka je osnovici DZ, a trougao HBG jednak trouglu DEZ, i ostali uglovi su jednaki ostalim uglovima koji se nalaze spram jednakih strana [I. 4]. Prema tome je ugao HGB jednak uglu DZE. Ali je po pretpostavci ugao DZE jednak uglu BGA. Prema tome bi ugao BGH bio jednak uglu BGA, manji većem, a to je nemoguće. Na ovaj način AB nije nejednako DE, dakle jednako je. Ali i BG je jednako EZ. Prema tome su dve strane AB, BG jednake dvema stranama DE, EZ, i to odgovarajućim, i ugao ABG jednak je uglu DEZ, usled čega je i osnovica AG jednaka osnovici DZ i preostali ugao BAG jednak preostalom uglu EDZ [I. 4].
Neka su sad jednake strane, koje su spram jednakih uglova, naime AB jednaka strani DE. Tvrdim da su i ostale strane jednog jednake ostalim stranama drugog, i to odgovarajućim, naime strana AG strani DZ, strana BG strani EZ i preostali ugao BAG jednak je preostalom uglu EDZ.
Ako pak BG nije jednako EZ, onda je jedna od njih veća. Neka je veće, ako je moguće, BG; tada se na BG prenese BQ jednako EZ, i povuče AQ. Pošto je BQ jednako EZ, a AB jednako DE, to su dve strane AB, BQ jednake dvema stranama DE, EZ, i to odgovarajućim, a čine jednake uglove. Pa prema tome je osnovica AQ jednaka osnovici DZ, i trougao ABQ jednak trouglu DEZ, i ostali uglovi jednaki ostalim uglovima, koji su spram jednakih strana [I. 4]. Prema tome je ugao BQA jednak uglu EZD. Ali je ugao EZD jednak uglu BGA. Usled toga bi u trouglu AQG spoljašnji ugao BQA bio jednak unutrašnjem nesusednom BGA, a to je nemoguće [I. 16]. Na ovaj način BG nije nejednako EZ, znači da je jednako EZ. Ali je i AB jednako DZ. Prema tome su dve strane AB, BG jednake dvema stranama DE, EZ, i to odgovarajućim, i one grade jednake uglove, i osnovica AG jednaka je osnovici DZ, i trougao ABG jednak trouglu DEZ i preostali ugao BAG jednak preostalom uglu EDZ [I. 4].
Na ovaj način, ako su kod dva trougla dva ugla jednog jednaki dvama uglovima drugog, i to odgovarajućim, i jedna strana jednog jednaka jednoj strani drugog ili ona na kojoj su jednaki uglovi ili ona što je spram jednog od jednakih uglova, onda su i ostale strane jednake ostalim stranama, i to odgovarajućim, i preostali ugao preostalom uglu. A to je trebalo dokazati.